The Role of Dimension in the Online Chasing Problem

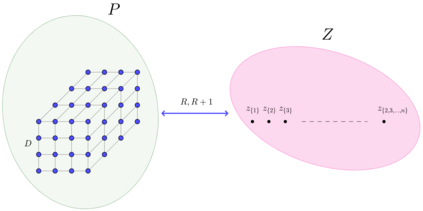
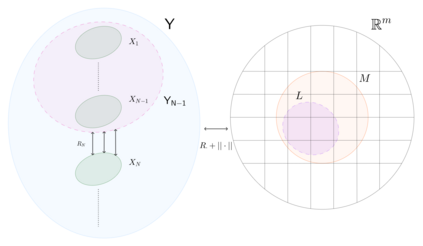
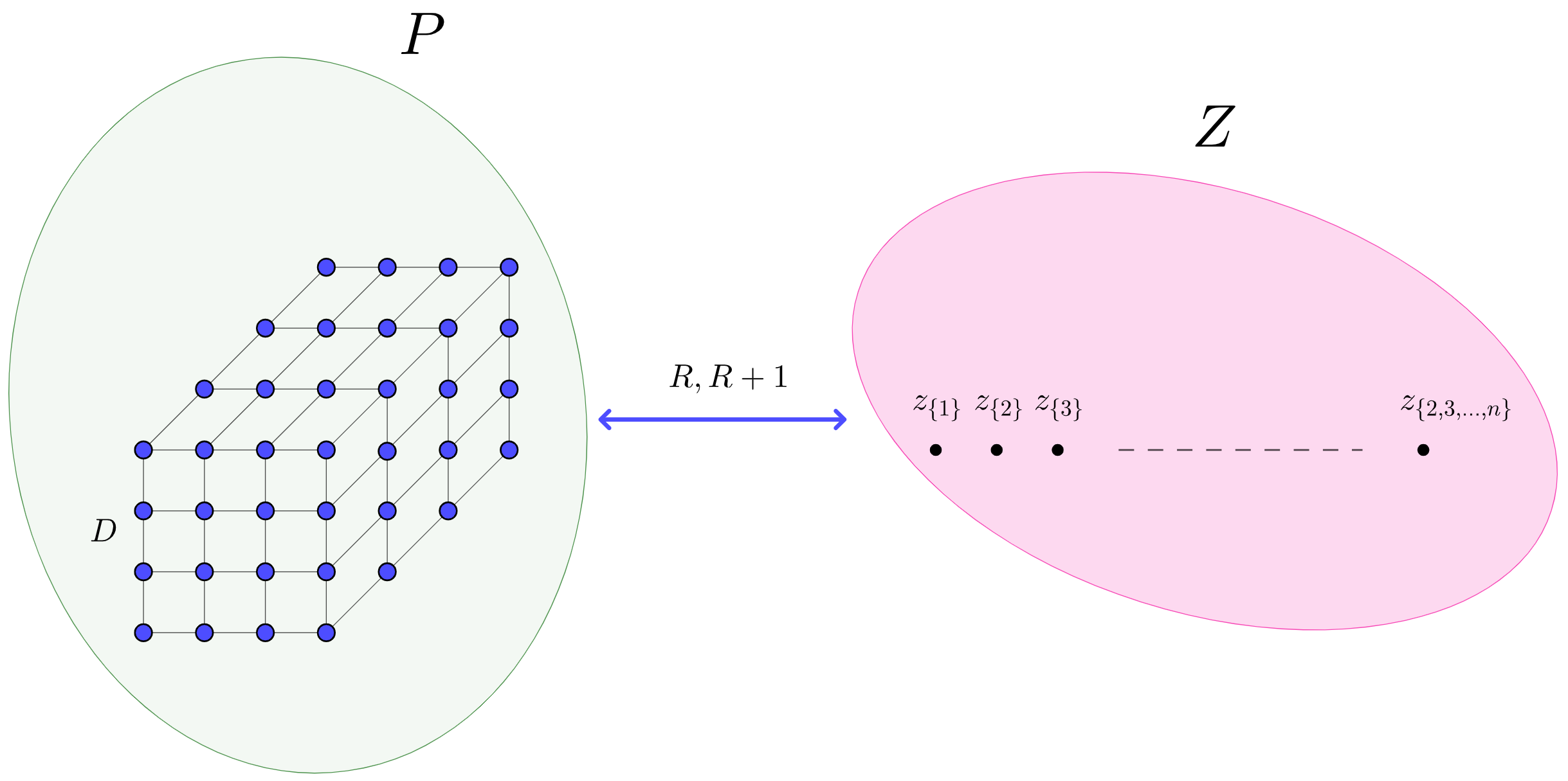
Let $(X, d)$ be a metric space and $C \subseteq 2^X$ -- a collection of special objects. In the $(X,d,C)$-chasing problem, an online player receives a sequence of online requests $\{B_t\}_{t=1}^T \subseteq C$ and responds with a trajectory $\{x_t\}_{t=1}^T$ such that $x_t \in B_t$. This response incurs a movement cost $\sum_{t=1}^T d(x_t, x_{t-1})$, and the online player strives to minimize the competitive ratio -- the worst case ratio over all input sequences between the online movement cost and the optimal movement cost in hindsight. Under this setup, we call the $(X,d,C)$-chasing problem $\textit{chaseable}$ if there exists an online algorithm with finite competitive ratio. In the case of Convex Body Chasing (CBC) over real normed vector spaces, (Bubeck et al. 2019) proved the chaseability of the problem. Furthermore, in the vector space setting, the dimension of the ambient space appears to be the factor controlling the size of the competitive ratio. Indeed, recently, (Sellke 2020) provided a $d-$competitive online algorithm over arbitrary real normed vector spaces $(\mathbb{R}^d, ||\cdot||)$, and we will shortly present a general strategy for obtaining novel lower bounds of the form $\Omega(d^c), \enspace c > 0$, for CBC in the same setting. In this paper, we also prove that the $\textit{doubling}$ and $\textit{Assouad}$ dimensions of a metric space exert no control on the hardness of ball chasing over the said metric space. More specifically, we show that for any large enough $\rho \in \mathbb{R}$, there exists a metric space $(X,d)$ of doubling dimension $\Theta(\rho)$ and Assouad dimension $\rho$ such that no online selector can achieve a finite competitive ratio in the general ball chasing regime.