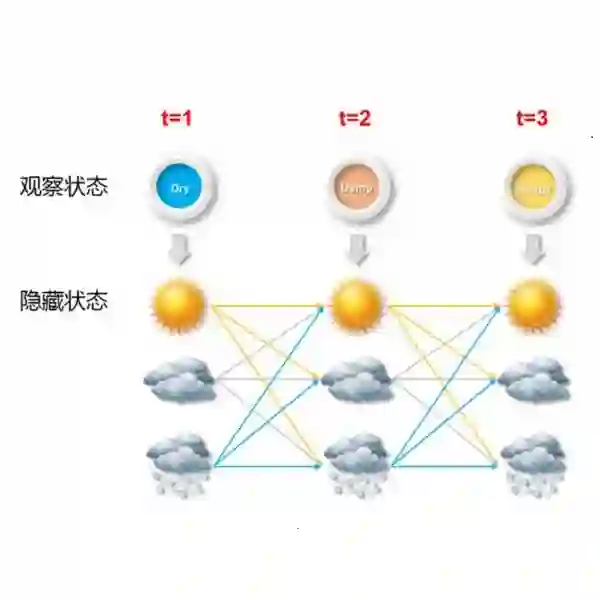
We consider learning the structures of Gaussian latent tree models with vector observations when a subset of them are arbitrarily corrupted. First, we present the sample complexities of Recursive Grouping (RG) and Chow-Liu Recursive Grouping (CLRG) without the assumption that the effective depth is bounded in the number of observed nodes, significantly generalizing the results in Choi et al. (2011). We show that Chow-Liu initialization in CLRG greatly reduces the sample complexity of RG from being exponential in the diameter of the tree to only logarithmic in the diameter for the hidden Markov model (HMM). Second, we robustify RG, CLRG, Neighbor Joining (NJ) and Spectral NJ (SNJ) by using the truncated inner product. These robustified algorithms can tolerate a number of corruptions up to the square root of the number of clean samples. Finally, we derive the first known instance-dependent impossibility result for structure learning of latent trees. The optimalities of the robust version of CLRG and NJ are verified by comparing their sample complexities and the impossibility result.
翻译:我们考虑学习高山潜伏树模型的结构,并在其中一部分被任意腐蚀时进行矢量观测。 首先,我们展示了RG(RG)和Chow-Liu Recursive Group(CLRG)的样本复杂性,而没有假设实际深度与观察到的节点数量相连接,大大概括了Choi等人(2011年)的结果。我们表明CLRG的周-Liu初始化极大地降低了RG的样本复杂性,从树直径直径的指数化到隐藏的Markov 模型(HMM)直径的对数性。 其次,我们通过使用节流的内产产品,将RG、CLRG、Neighbor Comiting(NJ)和Spectral NJ(SNJ)的样本进行强化。这些坚固的算法可以容忍大量腐败,直到清洁样品的平方根。 最后,我们从结构上得出第一个已知的无法根据实例学习潜在树木的结果。 通过比较样品和不可能的结果,可以核实CLRG和NJ的最佳版本。