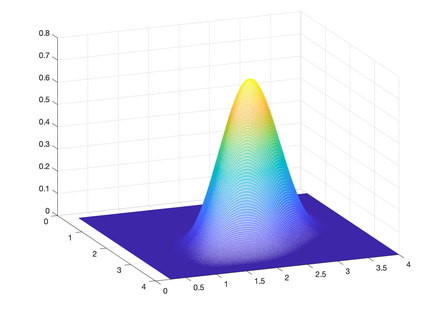
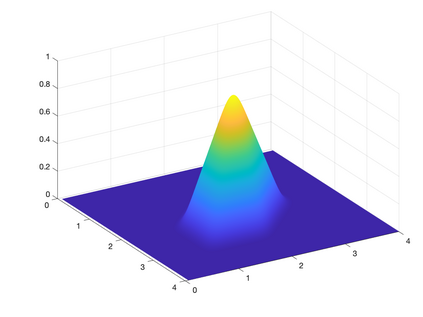
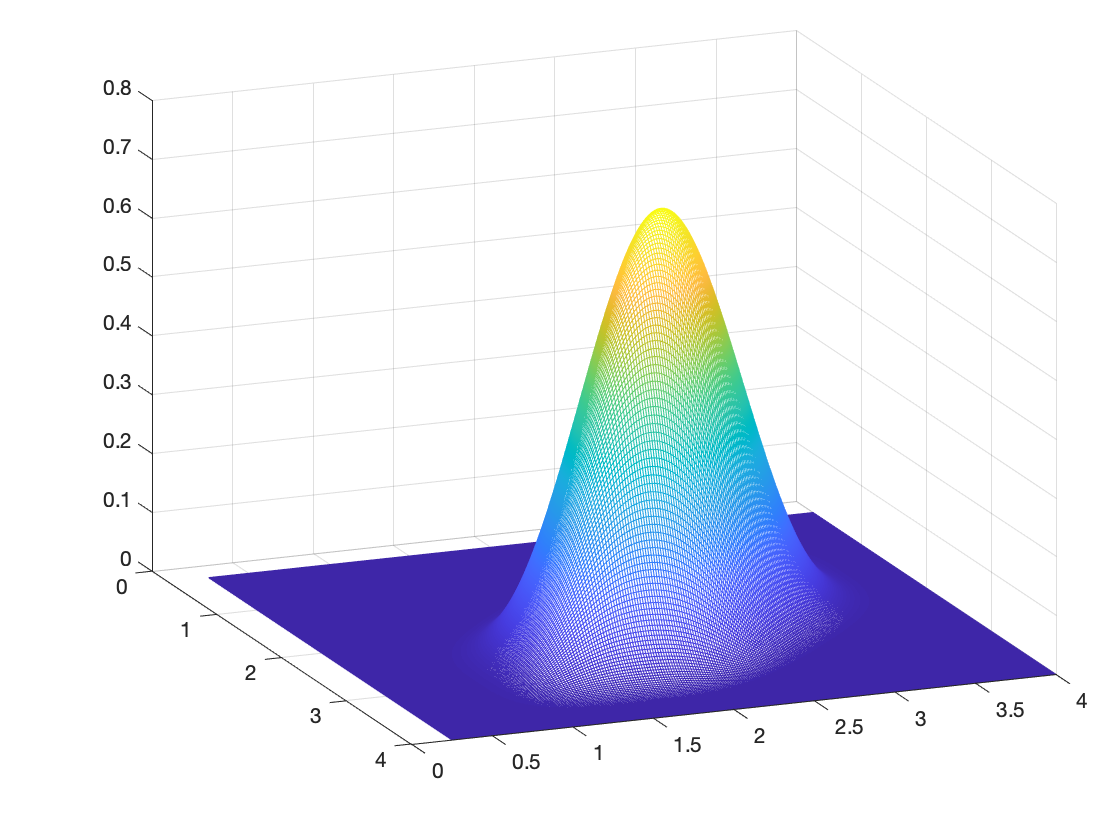
This paper discusses the generation of multivariate $C^\infty$ functions with compact small supports by subdivision schemes. Following the construction of such a univariate function, called \emph{Up-function}, by a non-stationary scheme based on masks of {spline subdivision schemes} of growing degrees, we term the multivariate functions we generate Up-like functions. We generate them by non-stationary schemes based on masks of box-splines of growing supports. To analyze the convergence and smoothness of these non-stationary schemes, we develop new tools which apply to a wider class of schemes than the class we study. With our method for achieving small compact supports, we obtain, in the univariate case, Up-like functions with supports $[0, 1 +\epsilon ]$ in comparison to the support $[0, 2] $ of the Up-function. Examples of univariate and bivariate Up-like functions are given. As in the univariate case, the construction of Up-like functions can motivate the generation of $C^\infty$ compactly supported wavelets of small support in any dimension.
翻译:本文讨论由子系统提供小型支持的多变 $C ⁇ incinfty 函数的生成。 在通过子系统创建了这种叫做 emph{ supping- comporate 函数之后, 通过基于 {spline supplie suspide propose} 的更高度的 {splie susplie suspility} 遮罩的非静止机制, 我们用我们生成的类似功能来定义多变函数。 我们用基于 支持增长支持的 $ $ $ 的遮罩的非静止机制来生成这些功能。 为了分析这些非静止计划的趋同性和平稳性, 我们开发了新工具, 适用于比我们研究的级别更广泛的计划。 在使用我们实现小型集约支持的方法的情况下, 我们获得了支持 $ $ $ 、 1 ⁇ ⁇ supsilon 的顶级功能, 与支持的 $ $ $ $ $ 0. 2] 的顶级功能的顶级支持。 我们给出了非静态和 类似功能的例子。 在未受支持的任何小支持的波段中, 。