A Horseshoe Pit mixture model for Bayesian screening with an application to light sheet fluorescence microscopy in brain imaging

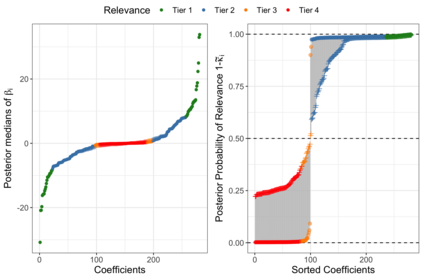
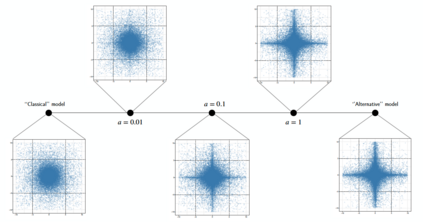
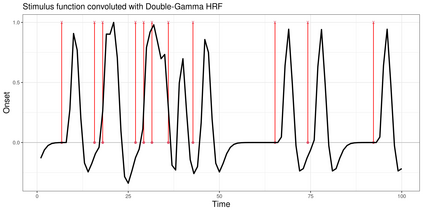
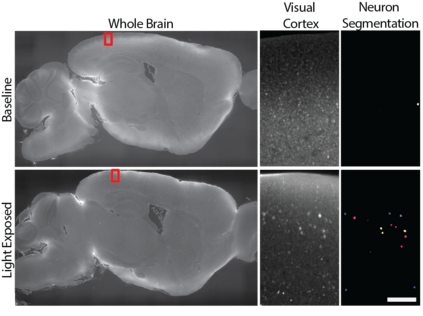
Finding parsimonious models through variable selection is a fundamental problem in many areas of statistical inference. Here, we focus on Bayesian regression models, where variable selection can be implemented through a regularizing prior imposed on the distribution of the regression coefficients. In the Bayesian literature, there are two main types of priors used to accomplish this goal: the spike-and-slab and the continuous scale mixtures of Gaussians. The former is a discrete mixture of two distributions characterized by low and high variance. In the latter, a continuous prior is elicited on the scale of a zero-mean Gaussian distribution. In contrast to these existing methods, we propose a new class of priors based on discrete mixture of continuous scale mixtures providing a more general framework for Bayesian variable selection. To this end, we substitute the observation-specific local shrinkage parameters (typical of continuous mixtures) with mixture component shrinkage parameters. Our approach drastically reduces the number of parameters needed and allows sharing information across the coefficients, improving the shrinkage effect. By using half-Cauchy distributions, this approach leads to a cluster-shrinkage version of the Horseshoe prior. We present the properties of our model and showcase its estimation and prediction performance in a simulation study. We then recast the model in a multiple hypothesis testing framework and apply it to a neurological dataset obtained using a novel whole-brain imaging technique.