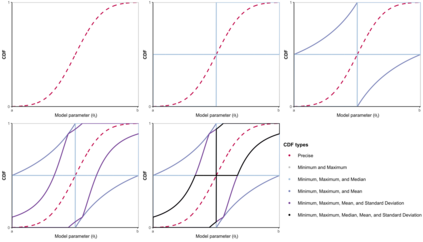
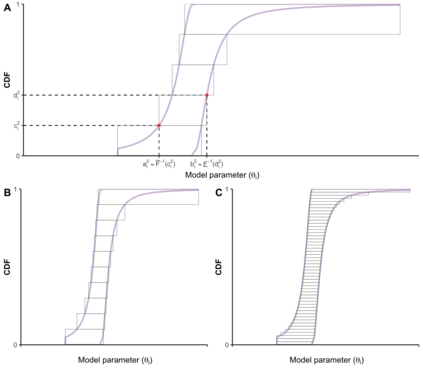
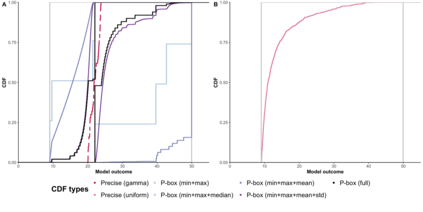
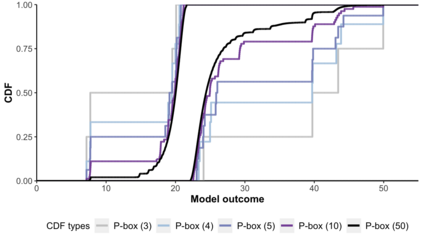
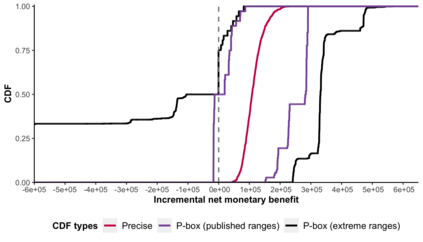
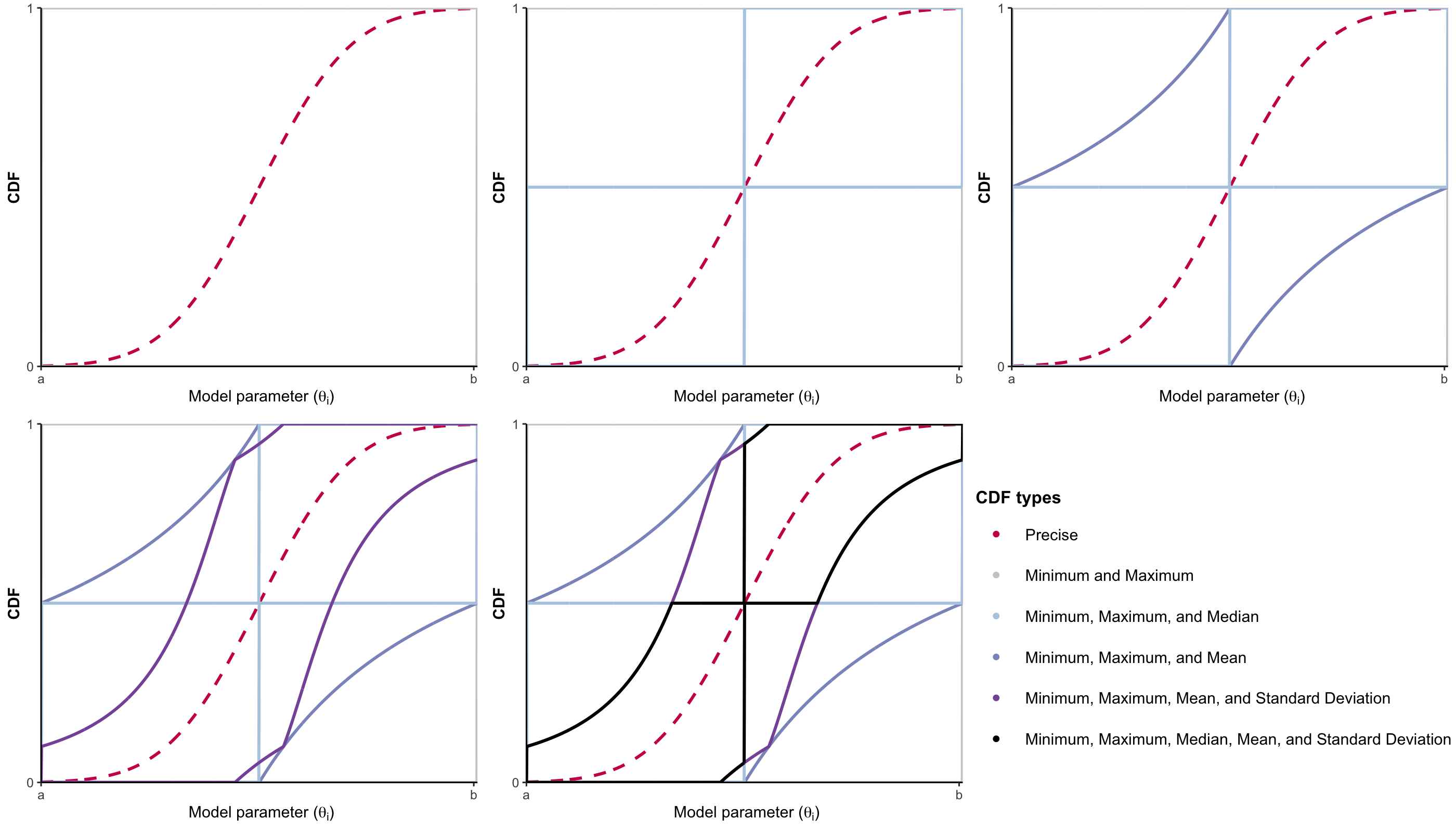
Decisions about health interventions are often made using limited evidence. Mathematical models used to inform such decisions often include uncertainty analysis to account for the effect of uncertainty in the current evidence base on decision-relevant quantities. However, current uncertainty quantification methodologies, including probabilistic sensitivity analysis (PSA), require modelers to specify a precise probability distribution to represent the uncertainty of a model parameter. This study introduces a novel approach for propagating parameter uncertainty, probability bounds analysis (PBA), where the uncertainty about the unknown probability distribution of a model parameter is expressed in terms of an interval bounded by lower and upper bounds on the unknown cumulative distribution function (p-box) and without assuming a particular form of the distribution function. We give the formulas of the p-boxes for common situations (given combinations of data on minimum, maximum, median, mean, or standard deviation), describe an approach to propagate p-boxes into a black-box mathematical model, and introduce an approach for decision-making based on the results of PBA. We demonstrate the characteristics and utility of PBA versus PSA using two case studies. In sum, this study provides modelers with practical tools to conduct parameter uncertainty quantification given the constraints of available data and with the fewest assumptions.
翻译:用于为此类决定提供信息的数学模型往往包括不确定性分析,以说明目前与决策有关数量的证据基础的不确定性的影响;然而,目前的不确定性量化方法,包括概率敏感性分析,要求模型家指定准确的概率分布,以代表模型参数的不确定性。本研究采用了一种新颖的推广参数不确定性、概率界限分析(PBA)的新办法,模型参数的概率分布不明的不确定性以未知累积分布函数(p-box)上下限的间隔值表示,不假定分配函数的具体形式。我们提供了用于常见情况的p-box公式(将最低、最高、中位、中位或标准偏差的数据组合起来),介绍了将p-box纳入黑盒数学模型的方法,并采用了基于PBA结果的决策方法。我们用两个案例研究展示了PBA相对于PSA的特征和实用性。我们提供了用于常见情况的p-box公式的模型模型,并提供了可用于量化不确定性的参数的实用工具。