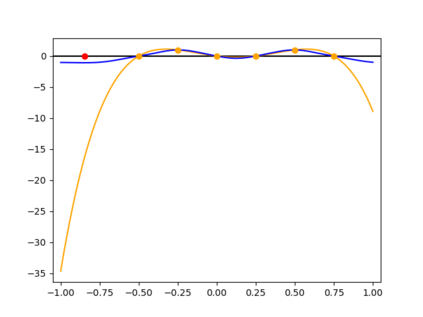
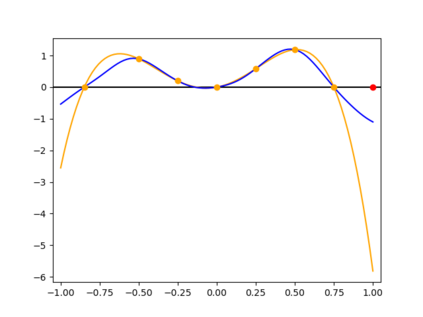
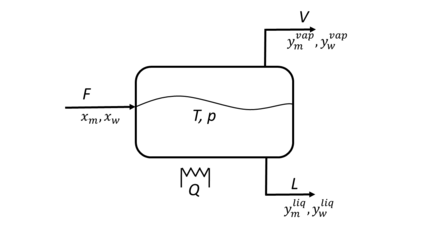
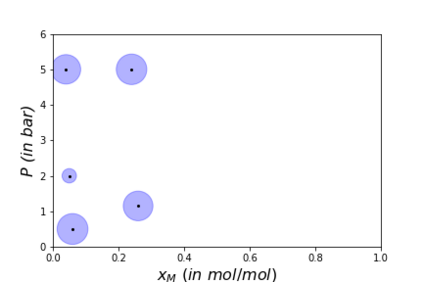
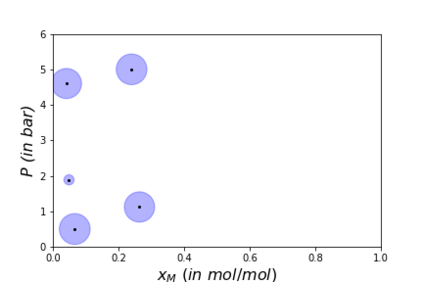
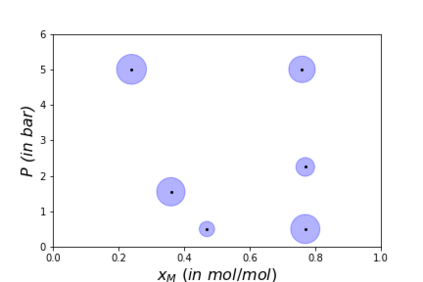
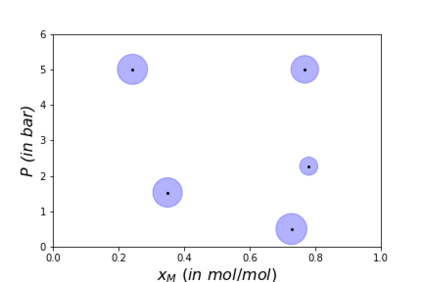
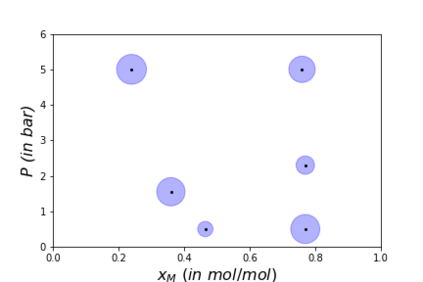
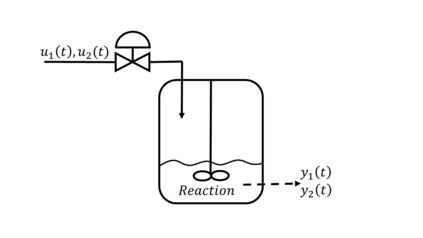
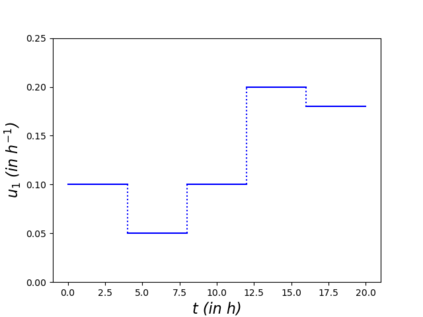
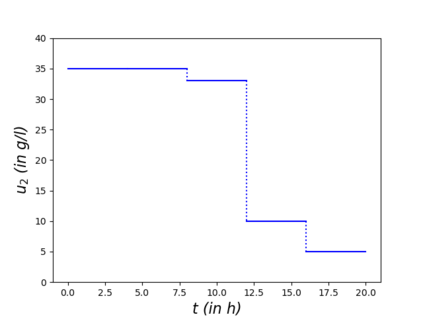
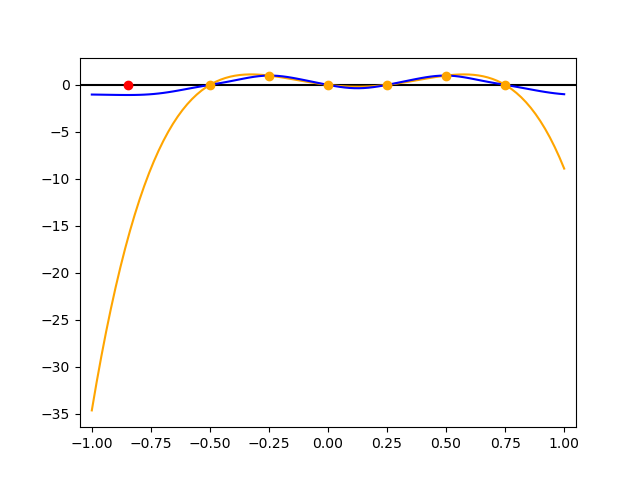
Algorithms which compute locally optimal continuous designs often rely on a finite design space or on repeatedly solving a complex non-linear program. Both methods require extensive evaluations of the Jacobian Df of the underlying model. These evaluations present a heavy computational burden. Based on the Kiefer-Wolfowitz Equivalence Theorem we present a novel design of experiments algorithm which computes optimal designs in a continuous design space. For this iterative algorithm we combine an adaptive Bayes-like sampling scheme with Gaussian process regression to approximate the directional derivative of the design criterion. The approximation allows us to adaptively select new design points on which to evaluate the model. The adaptive selection of the algorithm requires significantly less evaluations of Df and reduces the runtime of the computations. We show the viability of the new algorithm on two examples from chemical engineering.
翻译:计算当地最佳连续设计的算法常依赖于有限的设计空间或反复解决复杂的非线性程序。两种方法都需要对基本模型的Jacobian Df 进行广泛的评估。这些评估产生了沉重的计算负担。根据Kiefer-Wolfowitz等效理论,我们提出了一个新颖的实验算法设计,该算法在连续设计空间中计算最佳设计。对于这一迭代算法,我们把适应性的贝亚式采样方案与高斯进程回归结合起来,以近似设计标准的方向衍生物。近似法使我们能够适应性地选择新的设计点,用以评价模型。对算法的适应性选择要求大大减少对Df的评价,并缩短计算运行时间。我们用化学工程的两个例子来展示新算法的可行性。