图上的偏微分方程理论及其在图像处理中的应用

项目名称： 图上的偏微分方程理论及其在图像处理中的应用

项目编号： No.11461075

项目类型： 地区科学基金项目

立项/批准年度： 2015

项目学科： 数理科学和化学

项目作者： 辛巧

作者单位： 伊犁师范大学

项目金额： 40万元

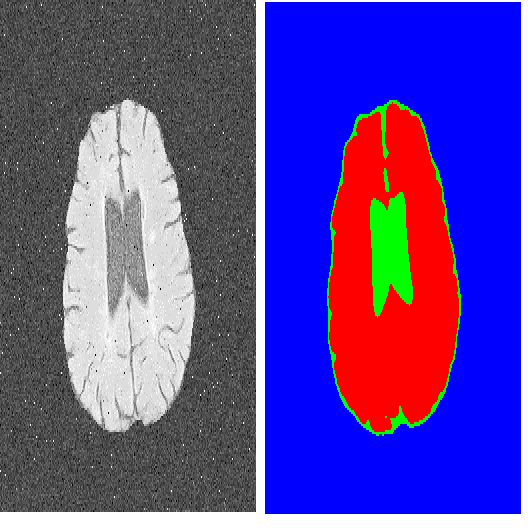
中文摘要： 图(Graph)是计算机科学、生物学、经济学、社会学等领域用来分析离散对象关系的重要工具。在项目致力于图上的偏微分方程如下三个方面的研究：（1）图上的偏微分方程解的存在、唯一性及其解的渐近行为，主要包括：熄灭、正性和爆破等性质；（2）利用图上的偏微分解的性质，讨论图的结构；（3）结合图上的p-Laplacain方程的非奇异性，建立更加有效的图像分割模型。

中文关键词： 非线性发展方程；解的爆破；适定性；数值模拟；图像分割

英文摘要： Graph is the important tool to analyze the relation between the discrete object in many fields, such as computer science, biology, economics, sociology etc. In this project, we mainly consider the following three problems for partial differential equations on graphs: (1)The existence and uniqueness on the solutions of partial differential equations on graphs, and also its asymptotic behavior, including the properties of extinction, positivity and blowup and so on; (2) Using the properties of partial differential equations on graphs, we will discuss the structures of the graphs; (3) Combining the nonsingular p-Laplacian on graphs, we propose more efficient model for image segmentation.

英文关键词： Nonlinear Evolution Equation;Blowup of sulutions;Well-posed;Numerical Simulation;Image Segementation