数据处理中的若干数学逼近方法问题研究

项目名称： 数据处理中的若干数学逼近方法问题研究

项目编号： No.11171299

项目类型： 面上项目

立项/批准年度： 2012

项目学科： 数理科学和化学

项目作者： 李松

作者单位： 浙江大学

项目金额： 48万元

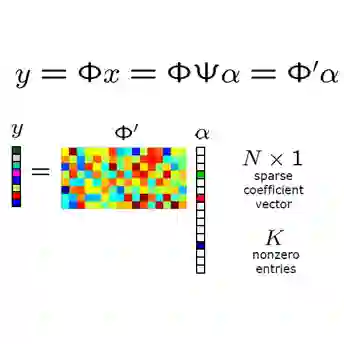
中文摘要： 小波分析理论是上个世纪八十年代中期发展起来的一个新的数学方法，到目前为止已经形成了系统的理论，在应用中也已取得了巨大的成功。近几年来，高度稀疏信号恢复问题得到了包括菲尔茨奖获得者T.Tao、J.Bourgain、美国科学院院士D.Donoho、小波分析权威I.Daubechies、世界数学家大会1小时报告人R.Devore及特邀报告人E.Candes等人的高度关注，他们证明了[1-5]：在一定条件下高度稀疏信号能用几乎最少的试验次数精确恢复，并也发展了一系列算法。然而，在实际问题中，大量的信号并不是高度稀疏的，甚至是不稀疏的。因此研究信号在特定基下的稀疏表示及其用稀疏信号来逼近非稀疏信号问题就变得十分重要了。项目将针对上述问题开展研究，研究内容包括：1、用小波分析方法研究信号的稀疏表示问题；2、用非线性逼近理论方法研究非稀疏信号的逼近问题及其恢复问题；3、利用随机理论研究随机信号的恢复问题

中文关键词： 小波分析；高维数据；稀疏表示；压缩感知；低秩矩阵恢复

英文摘要：

英文关键词： wavelet analysis；high dimensional data；sparse presentation；compressed sensing；low rank matrix recovery