FCS 论坛 | 孟德宇:误差建模原理
本内容为 Frontiers of Computer Science 公众号独家稿件,未经授权不得转载。授权合作请留言联系。
传统机器学习主要关注确定性信息的建模,而在复杂场景下,机器学习方法容易出现对数据噪音的鲁棒性问题,而该鲁棒性问题与误差函数的选择紧密相关。在Frontiers of Computer Science (FCS) 主办的“人工智能与机器学习”特别论坛上,西安交通大学教授、FCS 青年 AE 孟德宇,做了特邀报告“误差建模原理”。
报告聚焦于如何针对包含复杂噪音数据进行误差建模的鲁棒机器学习原理。这一原理已经在遥感影像、CT图像与高光谱图像的相关应用中取得良好效果,并有望引导出更多有趣的机器学习相关应用与发现。

孟德宇,西安交通大学数学与统计学院教授、博导。研究领域包括自步学习、误差建模、张量稀疏性等机器学习相关方向的研究。在国内外顶级学术期刊和会议发表论文 80 余篇,包括 IEEE Trans 论文 18 篇,CCF A 类会议 28 篇。曾担任 ICML、NIPS 等会议程序委员会委员,AAAI 2016、IJCAI 2017高级程序委员会委员,现担任国际学术期刊 Frontiers of Computer Science 青年 AE。

以下文稿内容根据孟德宇教授的实际报告内容整理,记录了报告的核心内容,以飨读者。
使用机器学习方法处理现实应用问题时,在大家使用的机器学习模型中,一般都要设定一个误差项。最常见的设定方法是直接用一个 L2 或 L1 范数误差函数形式。那么大家有没有思考过如何从数据中自动学习一个对于这个数据更为合适的误差函数呢?今天,我们就来谈谈这个问题。
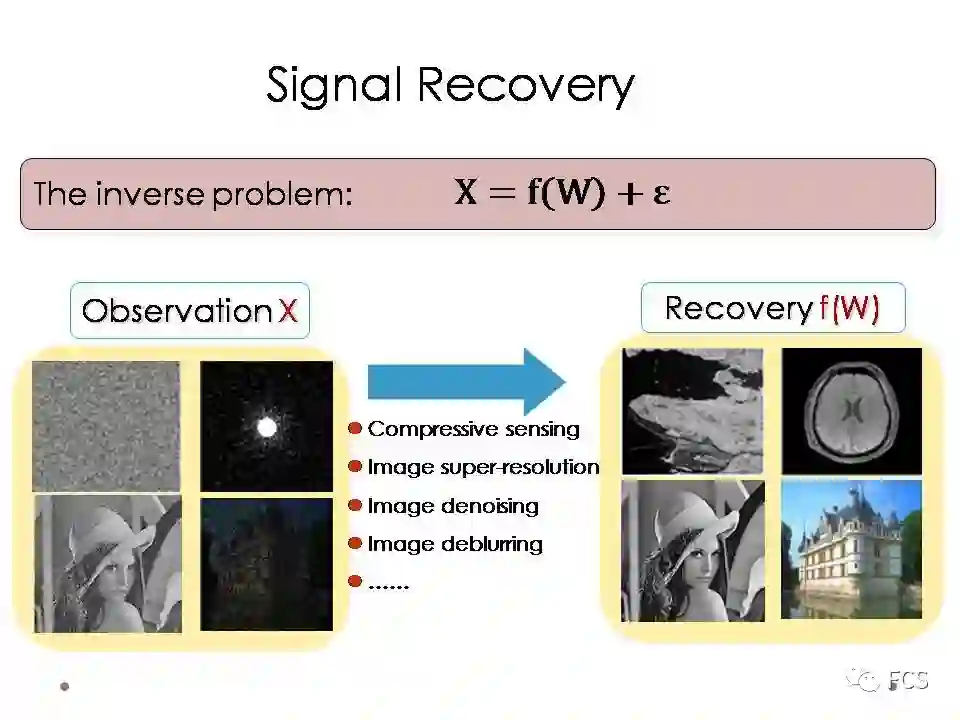
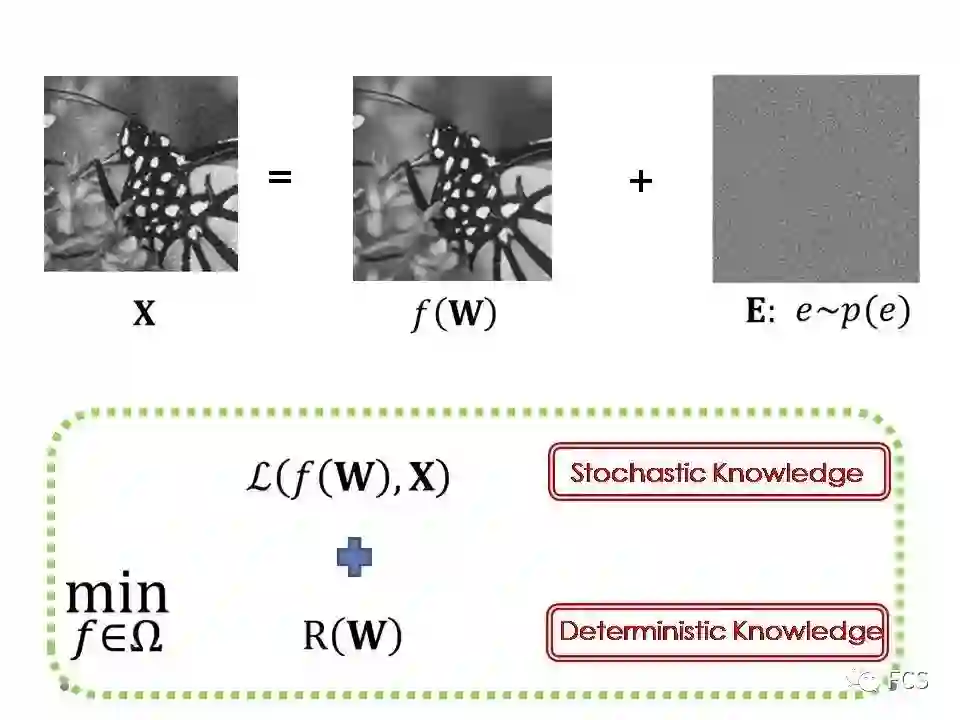
我们以信号恢复问题为例。当我拥有一个观测信号X,其真实信号是可以由一个结构函数f(W)来表达的,其中W指模型参数。信号恢复问题的目标是指,如何基于这样一个观测,去尽可能准确的恢复出其真实的信号f(W)。
这个问题的主要难度有两点:
第一是观测信号的自由度,也就是X的维度,可能是小于待求的模型参数W的自由度的。这意味着这个问题是不适定的,是一个无法准确求解的反问题;
第二是这个观测信号里还包含噪音,噪音的干扰使得我们的计算可能更加的不稳定。
很多的信号恢复,包括图像恢复问题,都可以理解为这个框架的特殊情形,比如说压缩传感,图像超分辨分析,图像去噪,图像去模糊等等。

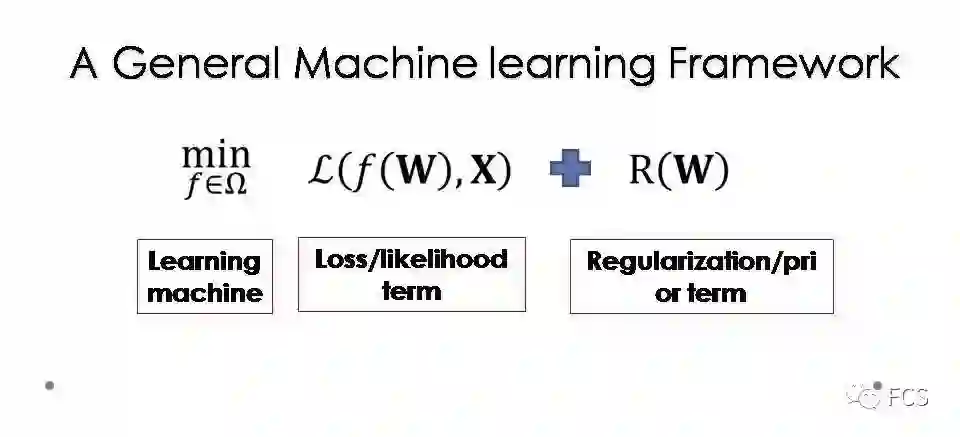
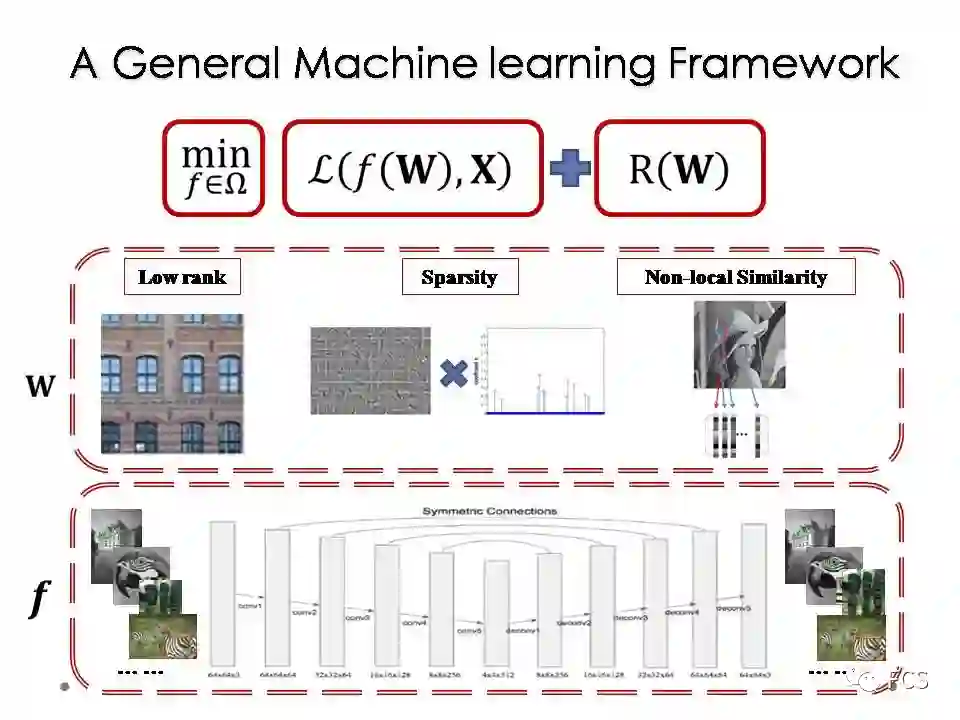
这个问题一般采用一个通用的机器学习模型来求解。模型中包含三个因素:
R(W)为正则项,编码了模型参数的先验信息,常采用的形式包括Ridge正则(即L_2范数正则)或稀疏正则(如L_1范数正则等);
Ω称为学习机,代表了一个预先设置的结构函数预选集合,其功能为对结构函数的学习范围进行约束;
L(f(W),X)为误差函数,度量了恢复信号f(W)对观测信号X的拟合程度,最常见的形式包括最小二乘误差(即L_2范数误差)与稳健误差(如L_1范数误差等)等。

介绍完这个机器学习的一般模型,我们可以简单的回顾一下信号恢复,特别是图像恢复技术的发展历史。这个历史可以非常粗略的分成两个阶段。
大约2010年之前,学者们主要关注的是如何合理的设置一个正则项形式,从而对模型参数的自由度进行限制,把不适定的问题变为适定。这个阶段有不少精彩的研究工作,比如在一定的条件下,可以证明稀疏性或者低秩性的正则约束可以诱导出一个严格精确的信号恢复。这些结论非常强,理论也很是优美。
但到了大概2010年之后,由于深度学习的强势崛起,对信号恢复技术也形成了很强的冲击。以图像去噪问题为例,可以提前做两个准备:一是准备大量的带噪图片与对应无噪图片的数据对,二是搭建一个结构合理的深度网络学习机,即对结构函数进行一个预先的设定。接下来,就可以利用深度学习优化技术,对这个网络涉及的参数进行训练。当在训练数据量充足的前提下,这套技术在很多图像恢复目标上,都达到了state-of-the-art的计算效果。
显然,这些技术主要考虑的是正则项与学习机,对误差函数的考虑相对较少,不少研究把误差函数的设定视为相对简单的步骤并不予以特别讨论和强调。在应用中,其作用是否可以真的忽略掉呢?为了回答这一问题,我们有必要对其内涵进行一个较为深入的探讨。

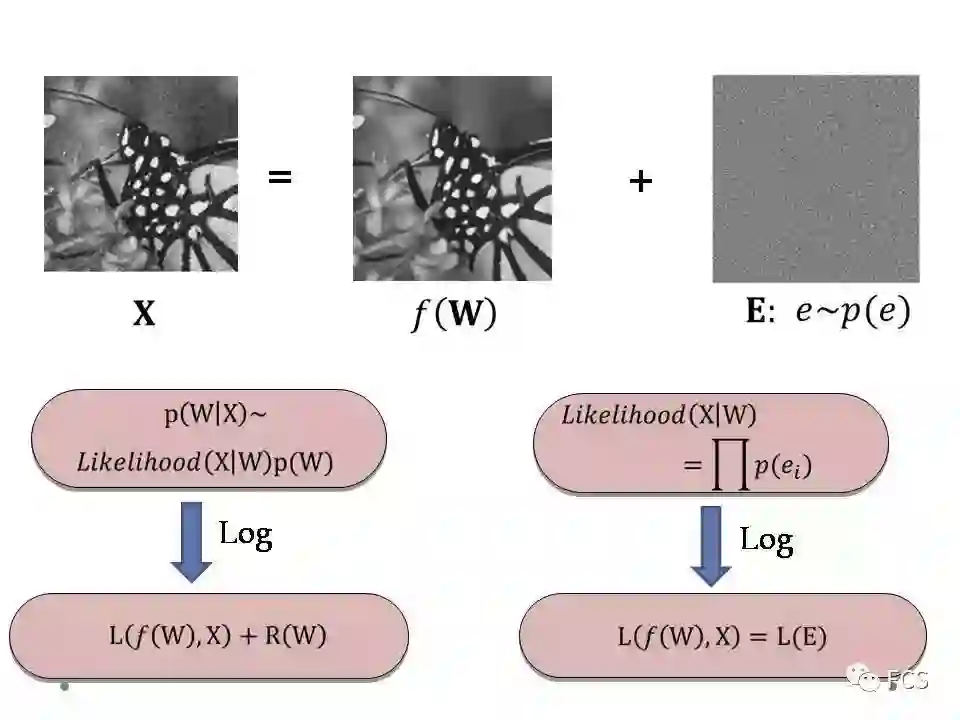
按之前所述,事实上一个观测信号中包含了两种信息,一种是真实的信号,其具有确定性的结构,我们称之为确定性信息;另一种为噪音,是随机性的,我们称之为随机性信息。
从最大后验的角度,信号恢复问题可以使用如下的方法进行刻画:模型参数W可通过计算一个后验分布的最大值获得。而该后验可等价于两项的乘积,一项为模型参数W的先验分布,其编码了W的先验结构信息;另一项为似然函数,其代表了在某一模型参数W下观测信号X的发生概率。
当我们对这一后验形式进行一个负Log变换,相乘就变成相加,最大就变成最小。对应这一最小化问题目标函数的两项,实际上恰好对应于机器学习模型的误差项与正则项。
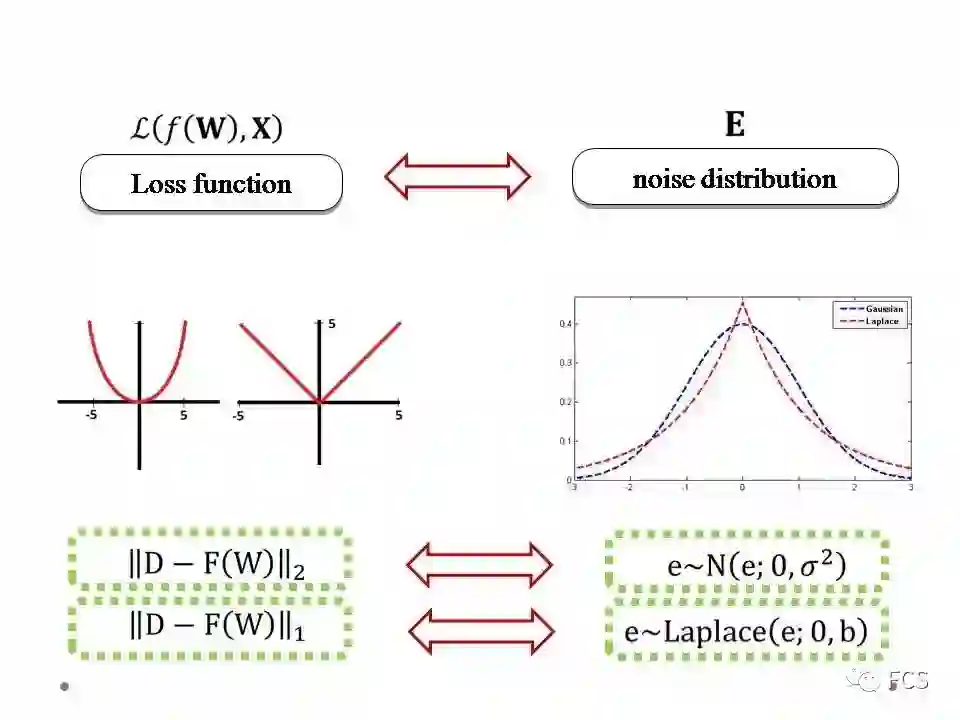
从这种意义来讲,其实误差函数和似然函数是具有对应关系的。由于似然函数刻画的是参数W下观测信号X的发生概率,而X中所有的随机性都来源于其随机性信息,即噪音,因此我们可以说,误差函数实际上是信号噪音的函数,其形式与噪音分布的类型具有一个对应关系。

因此,实际上机器学习模型的三个元素是各司其职,各自拥有特定的物理含义的。学习机和正则项编码的是信号的确定性信息,而误差项编码的是信号的随机性信息,即噪音。在这个报告里,我们想专门讲讲这一项。

按我们之前所介绍,误差函数和噪音分布其实存在一个对应关系。举最常见的两个例子:当我们使用L2或者L1误差的时候,事实上我们隐含假设了噪音分布是高斯或者拉普拉斯。

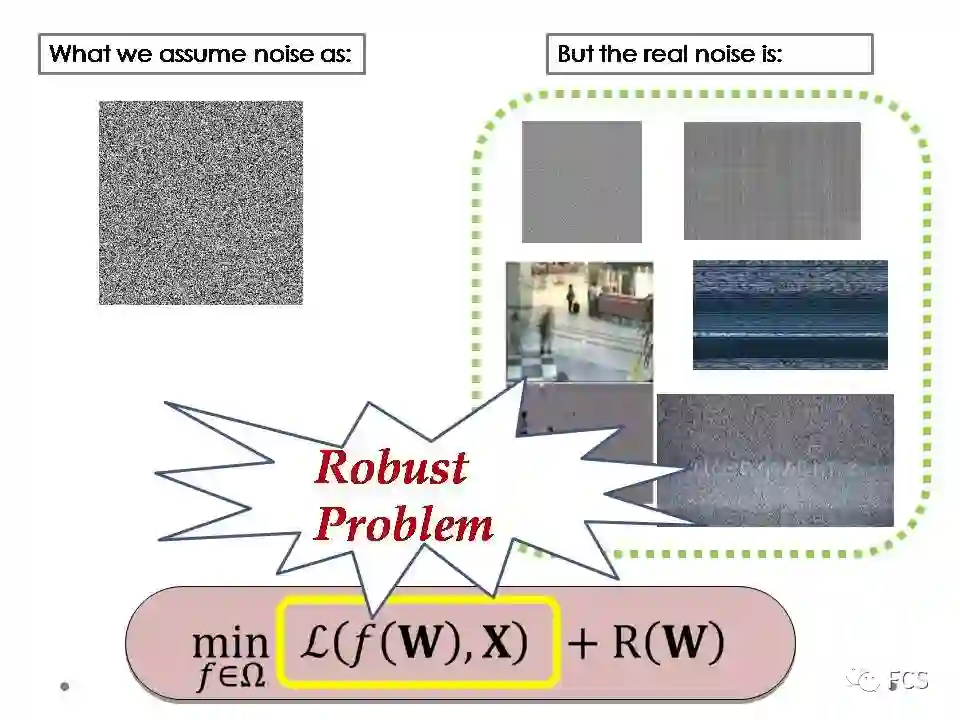
这一点可能意味着,当我们设定好一个固定的误差函数时,可能我们的模型就已经发生了一个主观性错误。因为固定的误差函数对应于某类噪音,但数据中蕴含的实际噪音类型,往往与我们假设的噪音分布相悖,也通常比我们假设的简单噪音更加的复杂。
所以,使用主观设定的简单误差函数,就很可能由于对实际复杂噪音不匹配,出现机器学习方法的计算不稳定问题。这个问题,我们可称之为鲁棒性问题,即误差函数的简单设定欠拟合了实际噪音的复杂性问题。

我们来看看有什么策略可以用来缓解这个随机性信息欠拟合的问题。

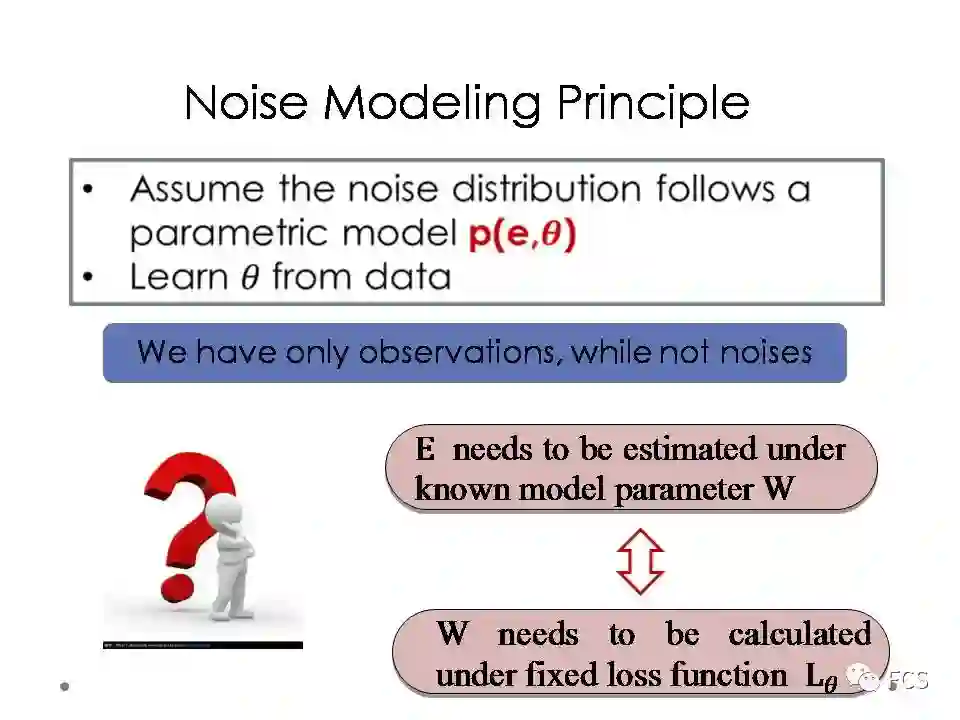
一个非常直接的想法是,我们用一个含参变量的分布来建模噪音分布,然后通过数据的噪音去学习其中的分布参数。然而,这个想法最大的问题是,我们的信息只有数据,却没有数据的噪音。
更具体的说,如果需要获得数据的噪音,我们就必须要知道模型参数W的值,然后通过X-F(W)来计算噪音;而如果想获得模型参数W的值,我们需要有一个固定的误差函数,从而使用对应的机器学习模型来求解W,但这个误差函数里面涉及的噪音分布参数,我们又必须通过数据噪音去学习。因此,这是一个鸡生蛋蛋生鸡的悖论问题。

但从机器学习的角度来看,这个问题实际上正好对应了一个迭代优化求解的算法。
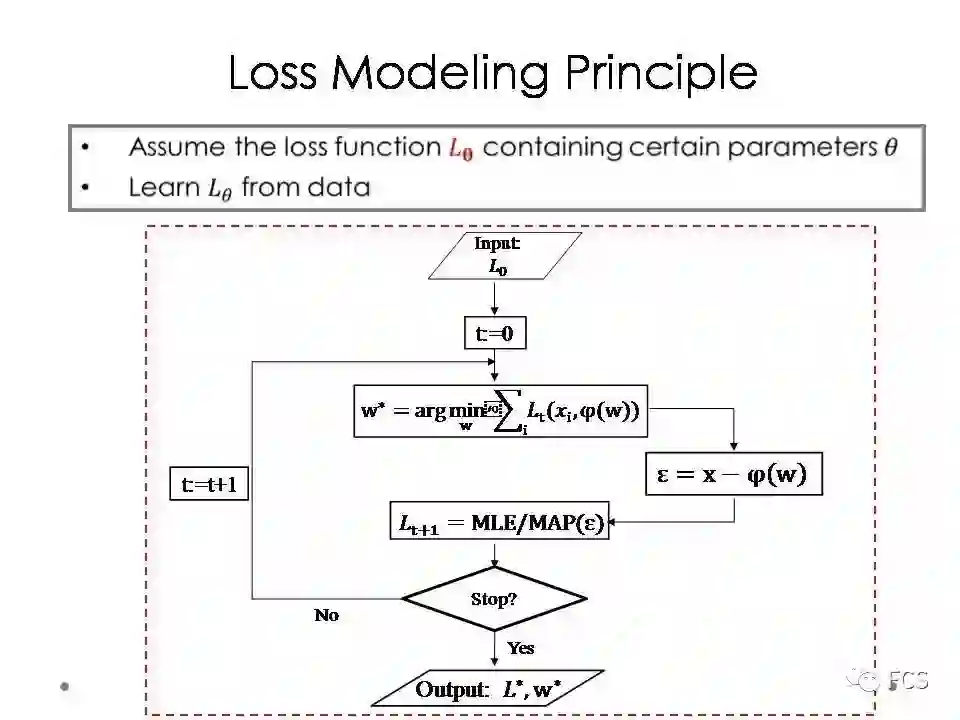
具体来说,首先我们先预设模型参数W,然后计算数据的噪音,基于噪音我们估计噪音分布的参数theta,然后获得对应于theta的固定误差函数,再对模型参数W进行重新估计。通过不断迭代这个过程,我们就可以得到模型参数W的同时,也得到最优的噪音分布参数theta.这种构造算法的基本思想,我们称之为噪音建模原理。
事实上,这个算法的背后,是有一个单调变化的最大似然,或最大后验,或最大熵的目标函数的。所以,这个迭代的过程是有一个目标函数通过理论健康的方式进行引导的。

我们也可以从误差的角度来解释这个算法。首先我们预设一个初始的误差函数,然后利用这个误差函数计算出模型参数,再计算数据的噪音,再通过噪音重新估计一个最优的误差函数。
不断迭代这个过程,最终输出的结果,除了模型参数之外,还有一个自适应匹配于训练数据噪音特点的误差函数。这种算法构造思想,我们称之为误差建模原理。

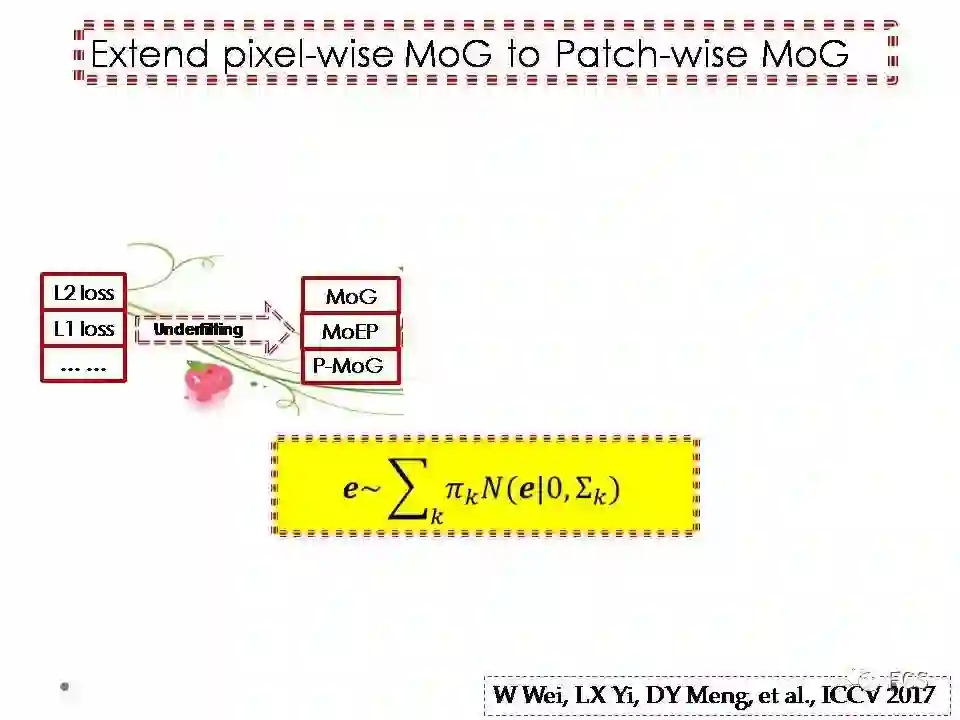
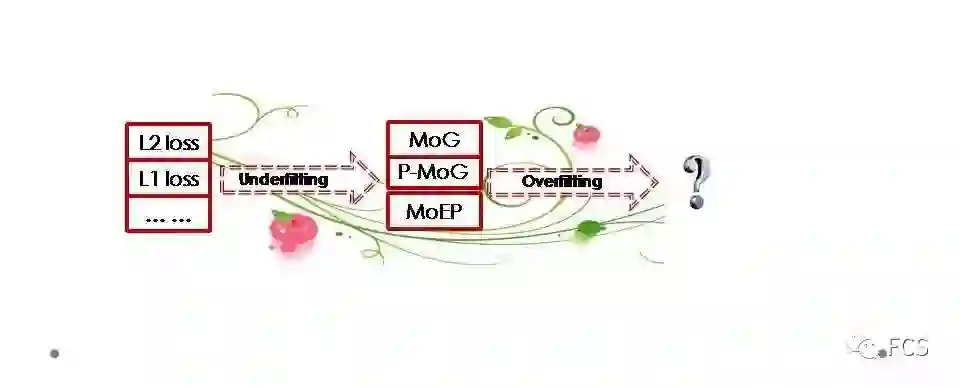
接下来的问题是如何设定这个含参变量的误差分布。最自然的选择,应该是混合高斯。

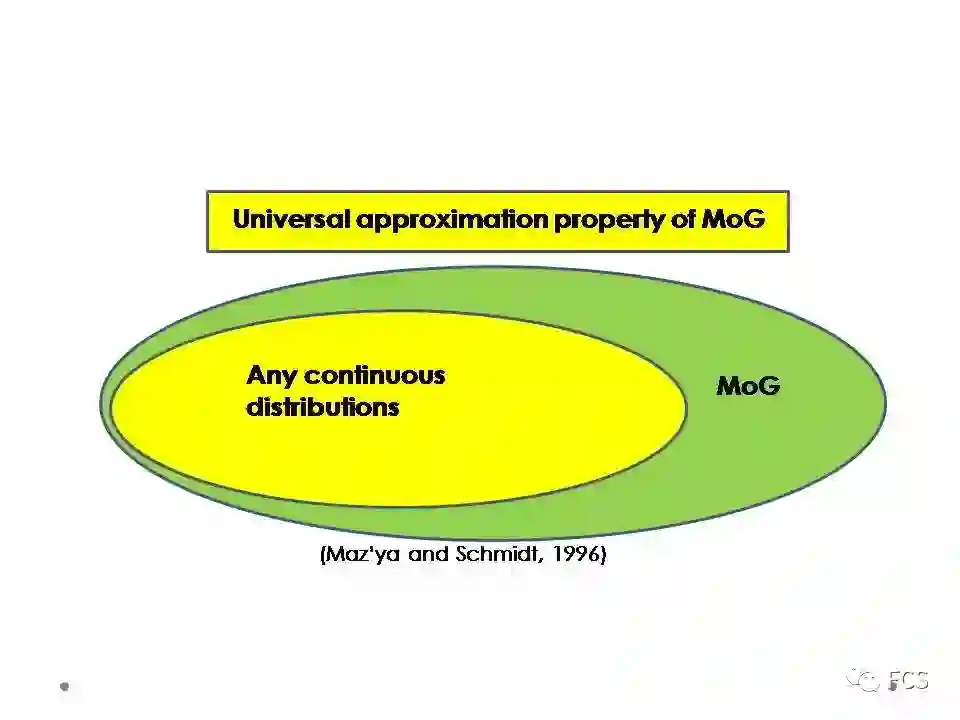
之所以选择混合高斯(MoG)建模噪音分布,主要有两个原因。一个是由于当我们不限制混合高斯的成分数目时,其具有对于连续分布的万有逼近性,而且还可以逼近很多种类的不连续分布;另一个主要从计算层面,混合高斯诱导的确定性模型之中,主要涉及具有平滑特性的L2范数,相对比较容易构造求解算法。

利用我们之前介绍的误差建模原理,我们可以构造基于MoG的噪音建模算法。首先初始化一个模型参数W,然后计算数据噪音,再估计混合高斯噪音的有关参数,最后在对应的误差函数下更新模型参数W。迭代这一过程直至收敛。
这一工作,主要是和我们小组的赵谦老师,和CMU的Fernando De la Torre教授合作完成的。

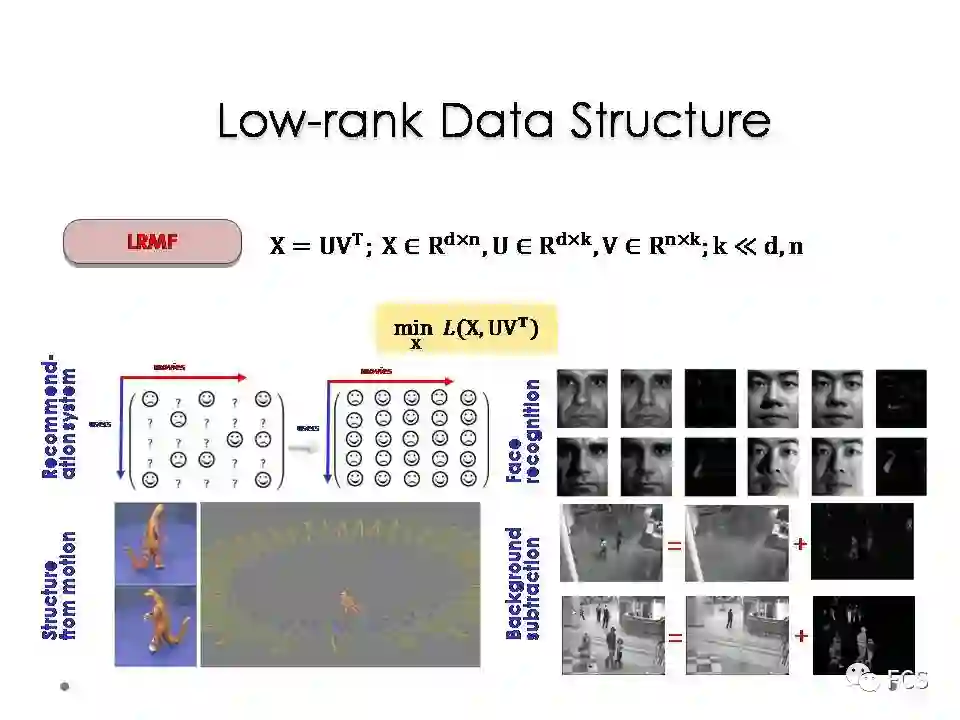
当我们把确定性信息用一个低秩先验的方式建模时,我们的问题对应于一个低秩矩阵恢复问题。这一问题在2010年左右是较为热点的一个研究方向。
但大多数现有方法都是基于L2或者L1误差函数来对问题进行求解,我们想通过用误差建模的方式改造这些方法,看能不能得到一些新颖有趣的实验效果。

首先一个例子是人脸建模。我们以Yale B这个数据库中的人脸为例。这些人脸的图片都已经做了很好的切割和对准,所以具有很强的相关性。
当我们把这些人脸图片拉成向量,堆叠成一个矩阵,则这个矩阵具有显著低秩性。所以利用低秩性先验可以把原数据中人脸的部分抽取出来,剩余的成分即对应噪音。我们用MoG噪音建模方法与传统低秩矩阵处理的方法进行效果对比时,发现一个有趣的现象,就是对一些具有大片黑色区域的人脸图片,我们的方法相对会有比较清晰的人脸恢复效果。

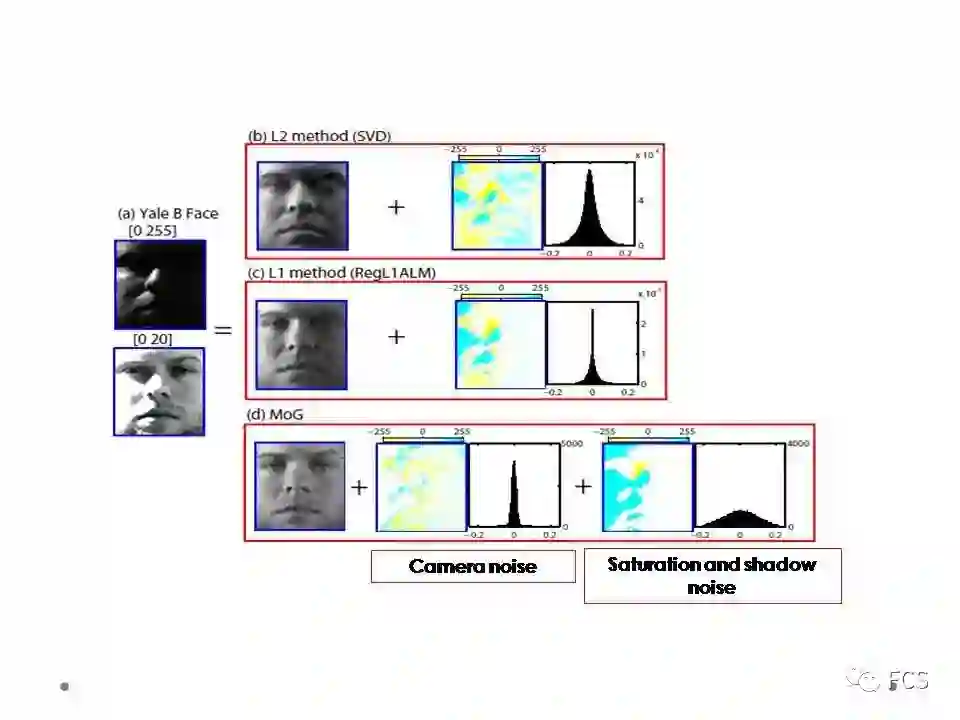
这一点实际上可以有一个物理意义解释的。其实人脸图片上包含的噪音还是比较复杂的。比如说当光线特别亮的时候,人脸会出现明显的亮斑,这种噪音叫做过饱和噪音;而当光线特别暗的时候,人脸图片会出现显著的暗斑,这种噪音叫做阴影噪音;而还有一种无法避免的镜像噪音,是由于光子成像原理引起的,无论照相设备多么先进都无法避免。但由于其一般幅度较小,所以在图片明亮的区域不是很明显,但在图像较为阴暗的部分,这种噪音就可以显现出来。
比如左边上方的图片,我们将其[0,20]的像素放亮到[0,255],就构成左边下方的图片。很明显其阴暗区域是有信息的,但较为模糊,这个模糊性就是来源于镜像噪音。
对于这么复杂的噪音分布,仅用一个高斯或者拉普拉斯是不能对其进行比较充分的刻画的。但如果使用两个混合成分的高斯,我们就可以自动获取到更为准确的噪音信息。小方差的高斯成分较为准确的对应到镜像噪音,而大方差的高斯比较准确的对应到过饱和和阴影噪音。更为准确的噪音提取,自然带来更为合理的人脸恢复。

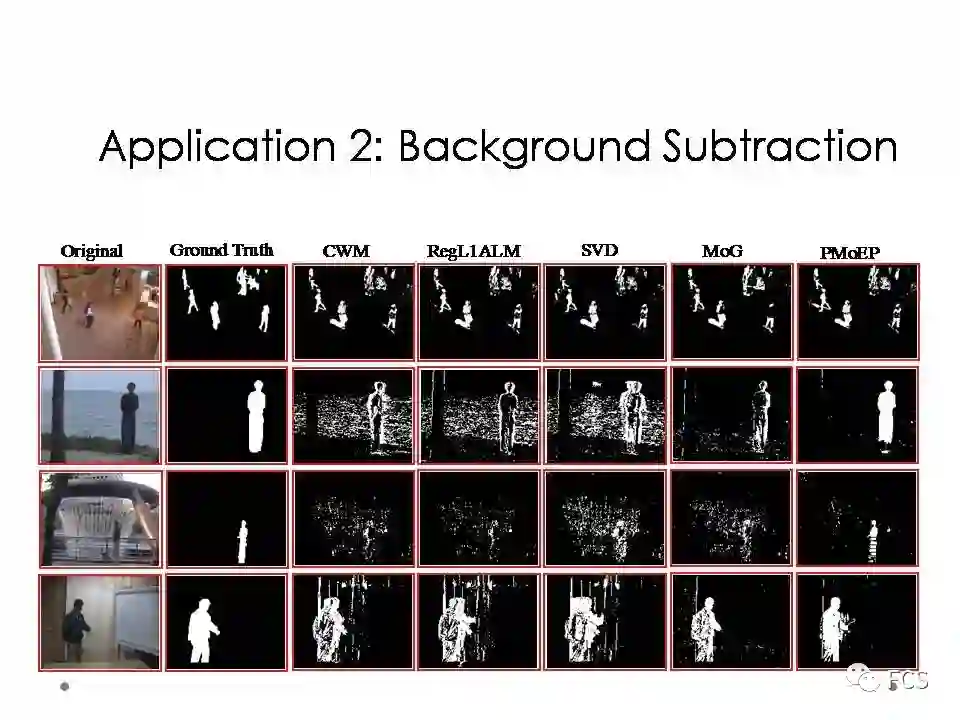
我们再举一个例子,就是视频的前背景分离,英文叫做background subtraction。即对应一个固定摄像头拍摄的视频,我们试图把它的前景目标和背景场景分离开来。
由于摄像头固定,所以视频的背景基本不移动,我们可以用一个低秩矩阵对这一确定性信息进行建模;而由于前景目标一般呈现一个块状的稀疏性,很多方法把其视为一个长尾分布的拉普拉斯噪音进行随机性信息建模,对应的误差函数就是L1范数的误差。

当使用我们的方法进行前背景分离时,我们也可以得到一些有趣的观察。最典型的一个现象就是传统方法一般只能分离出一个噪音分布,如高斯或拉普拉斯等,而我们的方法可以分离出多个噪音分布的成分来。
比如用三个成分的混合高斯对所示视频进行前背景分离时,获得的噪音包含三项,每项都有其显著的物理含义:最大方差的噪音对应于前景目标;第二大方法的噪音对应于前景目标的影子;而最小方差的噪音对应镜像噪音。

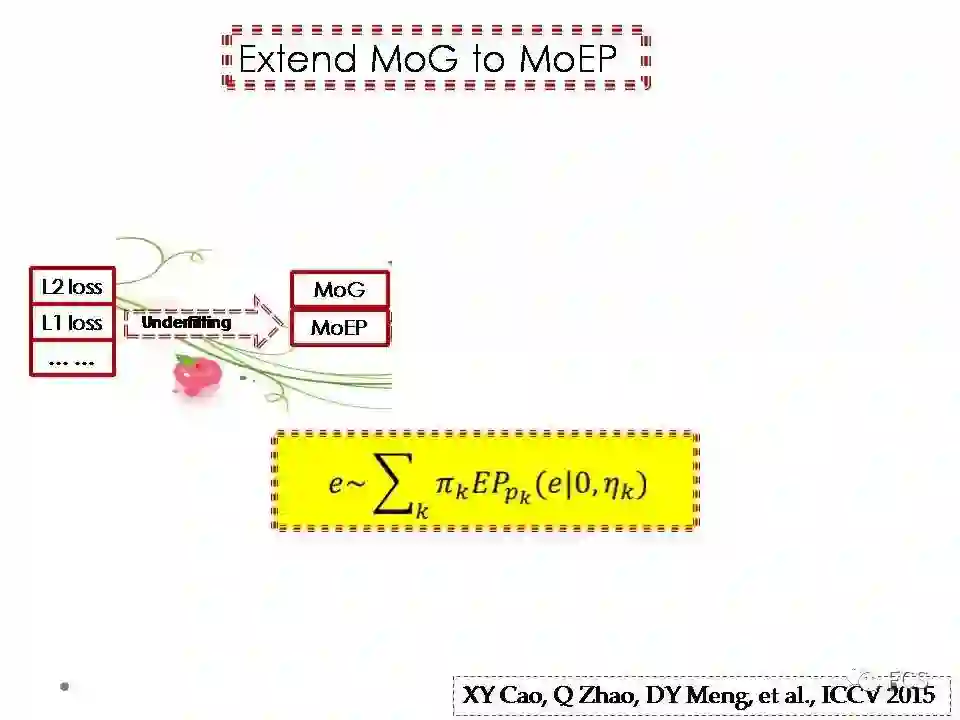
我们在2013,2014年陆续发表了混合高斯噪音建模的工作后,被问到最多的两个问题,一个是混合高斯的数目该怎么选,另一个就是有限个数的混合高斯对于复杂噪音的逼近能力似乎还是有限的问题。针对这两个问题,我们把混合高斯噪音建模改进为混合指数分布噪音建模的方法。

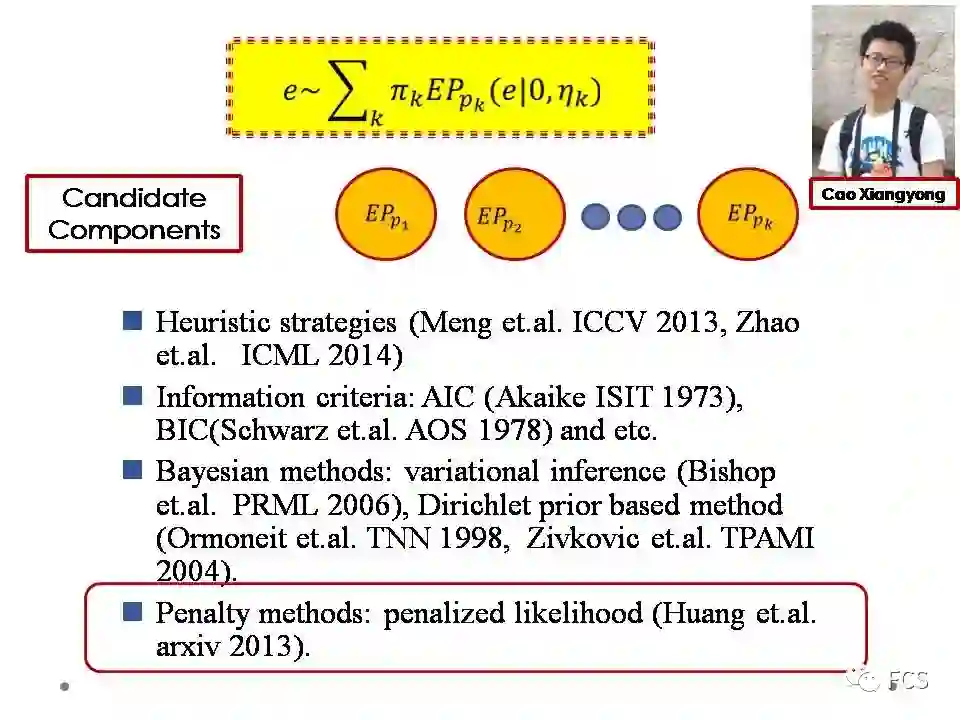
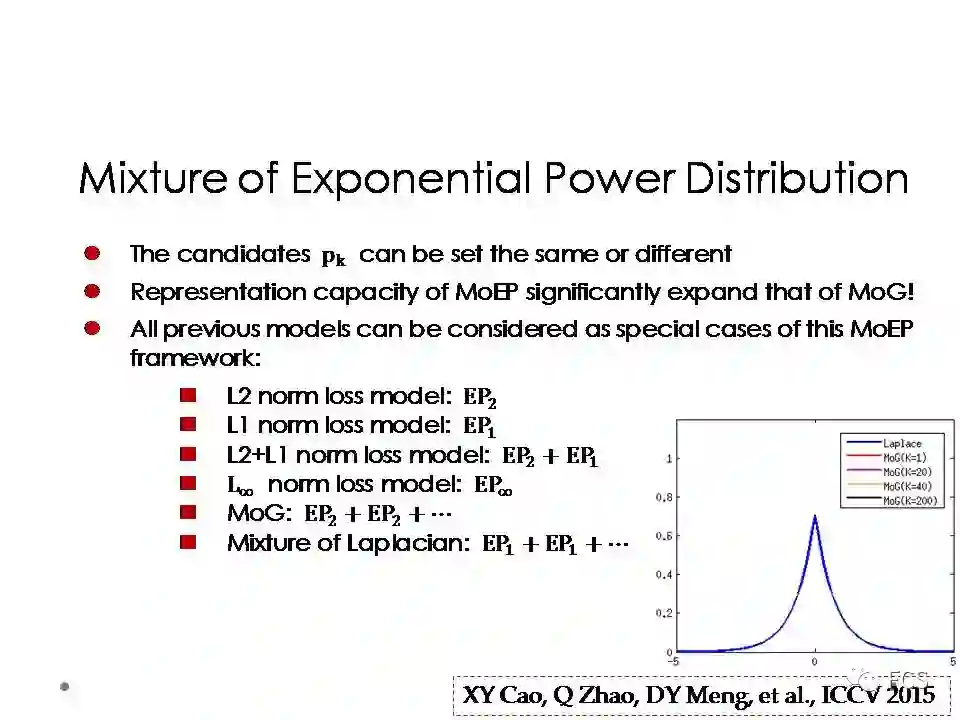
具体来说,我们首先设定一系列指数分布作为备选噪音成分,比如L0.1,L0.2,...,L10等。这里面的L2指数分布对应于高斯,L1指数分布对应于拉普拉斯。然后,我们采用特定的正则项,在这些备选噪音成分中进行稀疏的选择,从而对特定噪音分布的数据,选取出最为合适的指数分布成分。

这个方法很好的减弱了我们之前所提的两个问题:
一方面,混合指数分布的成分个数可以自动选择;
而另一方面,混合指数成分的备选多样性,使得该方法能够有效拟合更为广泛的噪音分布类型。
比如说如果要拟合拉普拉斯分布,理论上需要无限多个混合高斯成分,而如果使用这一噪音建模方式,只需要自动选取出一个L1指数分布成分,就可以做到完美拟合。
事实上,对于前几年比较常见的低秩矩阵分解/逼近的方法,大多数使用的误差函数,都是我们这一方法的特殊情形。这意味着这个方法对于噪音的拟合性,是比之前这些方法显著更强的。混合指数分布噪音建模的文章当时是发表在ICCV 2015上,被选为口头报告的论文。
这个工作主要是我们小组的曹相湧博士等人一同完成的。

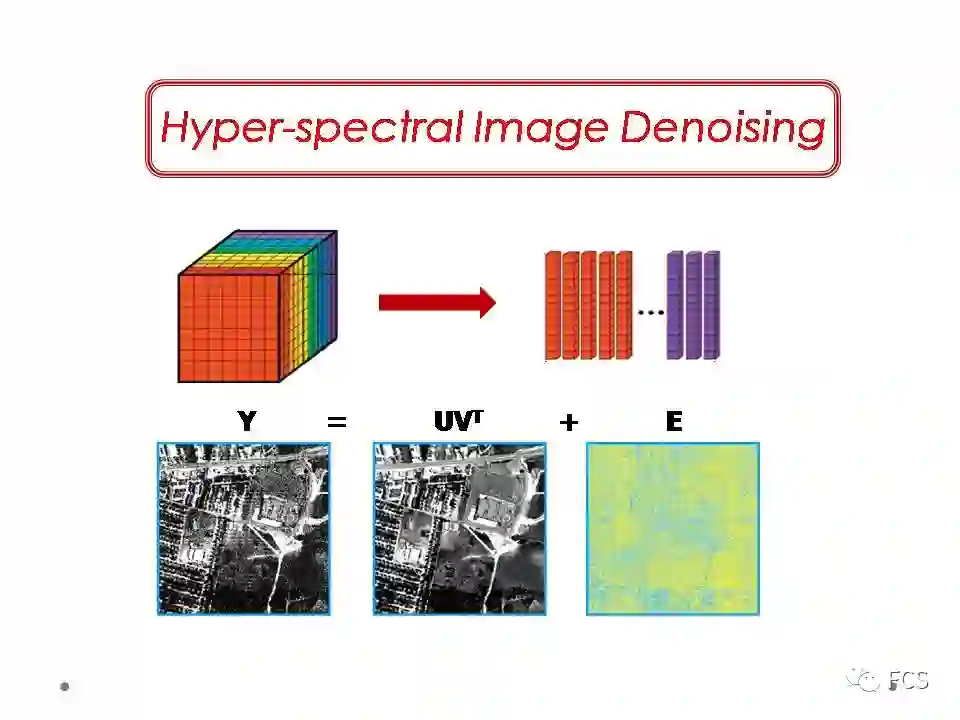
当时我们想尝试一些复杂噪音的具体示例,后来发现高/多光谱图像的去噪问题是一个很好的选择。对于一个高光谱图像,其包含多个谱段的信息,很多谱段实际上都具有较为复杂结构的噪音。由于其噪音的复杂性,我们决定拿这个类型的数据试试我们方法的效果。
我们对于确定性信息的建模,还是使用低秩性。也就是说,我们直接把每个谱段的图片直接拉成向量,然后依谱段把其堆砌为一个矩阵来进行处理。我们的方法没有用到高光谱图像的空间先验信息,包括空间平滑性,局部自相关性等,我们期望方法的效果,尽可能从随机性信息,即噪音的有效建模中得以体现。

最终的去噪效果也让我们非常满意,在当时做到了state-of-the-art。可以看到,即使在包含非常复杂噪音的谱段(如右下角),我们的方法也可以得到一个较为满意的恢复。这体现了噪音建模方法带来的算法鲁棒性,使其可以很有效的充分利用所有谱段的相关性信息,进行更准确的确定性信息提取。

之前所讲的用来建模噪音的分布函数,都是逐点独立同分布(iid)的。这种分布很难体现噪音的结构信息。但事实上,噪音实际上往往具有结构,比如说雨和雪,很明显其不仅具有很强的随机性,但同时又具有一定的结构信息。
再比如我之前看过一个综艺节目,叫做最强大脑,里面有些选手,可以从电视的雪花点,判断其来源于哪一台电视。当时偶然看了这个节目,还是有一些思想上的冲击。因为以前一直觉得雪花点是一个无信息的噪音,但这个节目实际上告诉我们,这个噪音是有结构性的。所以我们也想尝试做下带结构噪音建模的方法。

其实要体现噪音分布的结构并不复杂,我们只需要把之前的逐点混合高斯,改造为逐图像块的混合高斯。
也就是说,我们假设图像的每个小图像块(比如3*3的小块),是从一个逐块混合高斯(P-MoG)分布采样而来的。其分布形式与逐点的MoG相比,主要的差别是之前scalar形式的方差,转变为matrix形式的协方差矩阵。这个协方差矩阵的主成分方向信息,就体现了噪音的结构信息。

当时我们第一选择的应用,就是去雨。主要的原因是发现近几年在主流会议和期刊上关注去雨的工作还比较多,可以做充分的算法性能对比,所以觉得应该是一个比较能展示算法性能的合适的问题。这个工作,主要是我们小组的硕士生魏玮,易丽璇等人共同完成的。
当时我们对现有的去雨方法进行了一个较为全面的调研,之后我们就有了一些信心。主要是因为现有的方法大多都是把雨视为一个确定性信息的对象进行建模,比如说编码雨的色彩一致性等物理机理,雨随时空变化的连续性,雨局部结构的相关性等先验结构等等;近年来深度学习的方法也逐渐出现,通过收集很多带雨和不带雨的图像块进行训练,得到一个决策函数,直接将带雨的视频输入,得到一个不带雨的视频输出。
这些方法都是把雨视为一个确定性的信息,而由于除雨之外,我们还需要对视频背景,视频的前景目标也进行一个确定性信息的建模,这往往会带来编码模式的交叠,从而带来去雨不充分的问题。

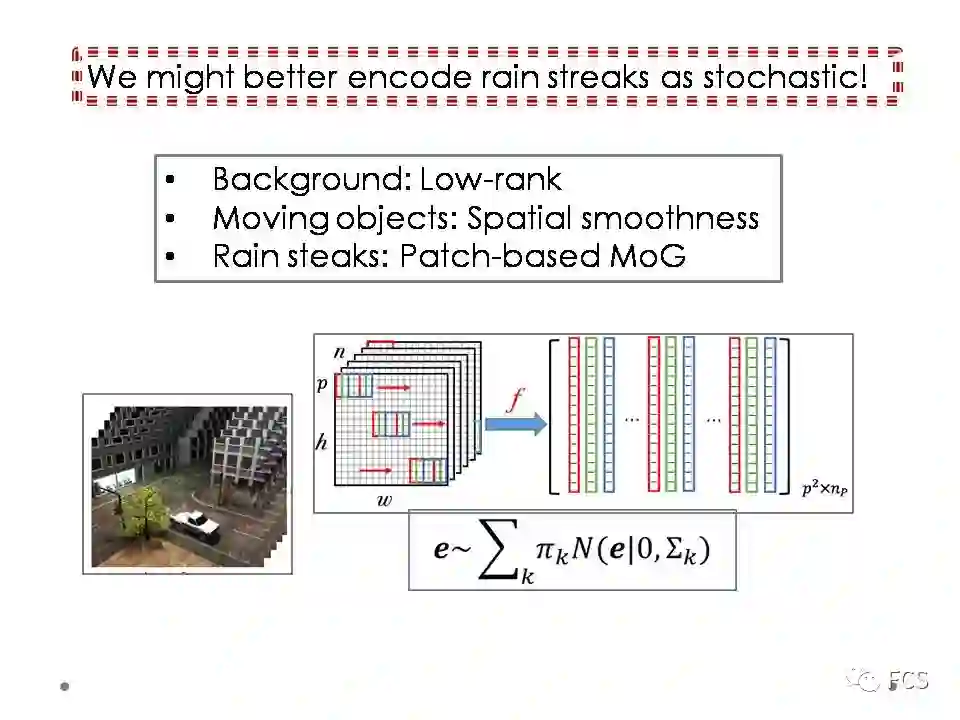
所以我们的主要想法就是把雨建模成为一个随机性的对象。具体来说,我们把视频分为三个部分分别进行建模。其中包含两个确定性的部分:背景用低秩性先验编码,移动前景目标用时空连续性与稀疏性进行先验编码。还包含一个随机性的雨的部分,用P-MoG进行噪音建模。

最终,我们可以形成一个较为简洁的优化模型,可以直接对一个带雨的视频,利用无监督的方式进行去雨。
相对于深度学习的方法,其一方面避免了对于训练数据的依赖,不需要耗费人力物力资源去收集带雨和不带雨的视频对;另一方面,其也避免了方法对于训练数据中雨的类型形成的bias问题,即当待去雨视频中的雨与训练数据中雨的类型不一致时,可能会出现算法的不稳定问题。

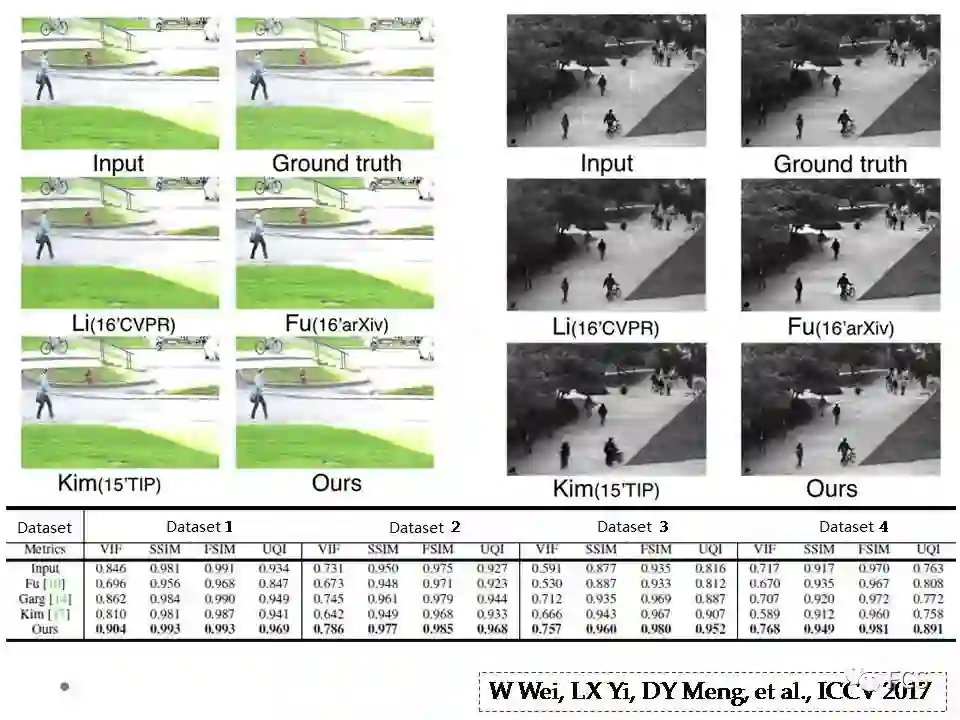
最终我们也从定性和定量的角度,都获得了state-of-the-art的效果。这个工作发表于今年的 ICCV。

我们可以观察一下各个方法提取出的雨的部分,可以很明显观察到,我们方法提取的雨更加准确,包含了更为少量的确定性信息,如视频背景,前景目标等。这也充分体现了算法对于确定性信息和随机性信息编码的互补性带来的效果。

这张图展示了算法的基本建模和有效性的机理。我们的方法可以把视频分为三个部分:
低秩的背景
时空连续且稀疏的前景
雨,其有包含三个成分,一个成分是像素与周边像素相关性较大的雨成分,对应于大块的雨点,一个成分是像素与周边像素相关性较小的雨成分,对应于幅度小一些的雨条,而还有一个成分是像素与周边像素相关性很小的噪音成分,这个噪音对应于视频镜像噪音的部分,更类似于一个逐点iid的噪音。
三个部分各自的编码都与实际情况较为吻合,而且具有很好的互补性。

看上去好像噪音建模的方法可以这样一直做下去,不管多么复杂的噪音,我们只需要把噪音分布假设的足够复杂,似乎都可以做到很准确的噪音逼近。
但这样做会出现一个非常严重的问题,就是我们建模的噪音逐渐变得复杂时,其拟合能力逐渐变得更强,此时它会不仅拟合掉我们预期的随机性信息,而且会逐渐拟合掉我们不期待的确定性信息。

这个现象是我们绝不愿看到的。如同我们对于确定性的信息建模,我们不希望其过于复杂,因为其不仅能拟合确定性信息,而且会逐渐拟合掉随机性信息一样。
这个问题的基本根源,其实就是机器学习领域的基本原则之一,奥卡姆的剃刀原理。
也就是说,当我们看到一个数据的时候,我们的大脑更倾向于用一种简单的模式对其进行编码识别,一方面我们希望用简单的确定性模式,如低秩,稀疏等,对其进行认识,另一方面,我们也希望用简单的随机性模型对其进行识别。
我想这就是为什么很多的工程领域,都非常喜欢iid高斯白噪音的根本原因,因为其是最简单的一种噪音分布形式。

非常不幸的是,在我们所处的大数据时代,我们面对的数据,其随机性信息往往既不是iid,也不是高斯白。
更为准确的说,需要我们处理的数据,正在由理想化的实验室环境,逐渐变化为随着时间,空间,维度等显著变化的开放式环境。这样的数据,无论是其确定性信息还是随机性信息,都不可能只用一个简单的模式进行建模。
实际上在去年的计算机大会上,多位专家已经提到了这个问题。我这里截取了周志华教授的两张slides。周教授认为,开放环境下,机器学习的鲁棒性是一个重要的研究问题。对周教授的观点,我深表认同。

因此,这里就出现了一个“简单”和“复杂”的矛盾。一方面,我们期待用简单的方式对噪音进行建模,但同时,现实数据噪音的复杂性又不得不要求我们对于噪音建模的复杂性有所考虑。那么,我们有没有办法实现一种折中的方案,既尽可能准确的拟合开放环境下形态复杂的数据噪音,而另一方面又能很好的对噪音的复杂性进行抑制从而减弱模型对噪音过拟合问题的发生呢?

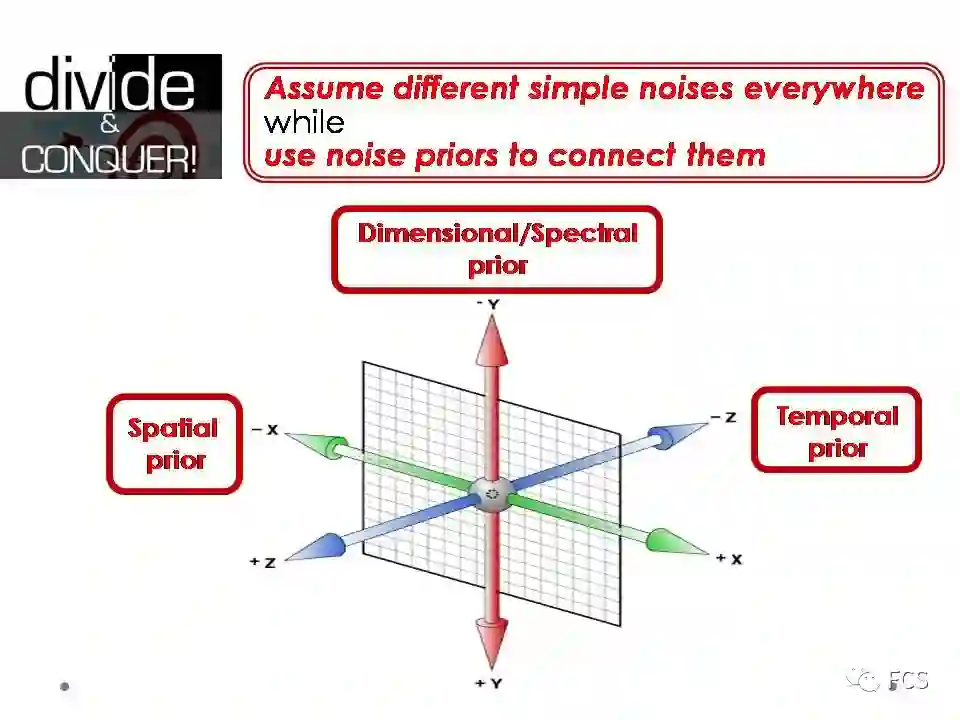
对这一问题的解决之道,也许就蕴藏在我们对于大数据的一种通用处理模式,分而治之,之中。具体来说,实际上我们在对数据噪音进行认识的时候,往往是既简单,又复杂的。
这里的“分”体现为两个方面:
一方面是指对于开放环境下数据的每个局部,其噪音分布应该是简单的,甚至往往可视为iid的高斯白噪音;
另一方面,这一噪音在不同的局部位置应该是不同的。这一局部分布的差异性体现了噪音复杂性,也体现了大数据本质的统计非iid特性。
而这里的“治”,体现为我们需要对这个复杂噪音的自由度,从空间,时间,维度等方面进行约束和限制,其物理含义为不同局部的噪音,存在空间,时间,维度等各方面的关联性,针对这一关联性的编码,可一定程度上抑制噪音建模的复杂性。通过这样的“分-治”策略,我们也许可以得到一个让噪音建模对开放性复杂数据进行有效刻画的折中方案。
所以,我们现在要解决的问题,就是对这样局部简单而有所差异的非iid噪音分布,如何去寻找并编码合理的时、空、维先验信息。

对空间,其实我们可以考虑噪音的空间一致性先验。这个意思是说,一个点如果噪音大,可能周边噪音幅度也比较大;而一个点如果噪音小,其周边可能也较为干净。
这个信息非常自然的,可以用马尔科夫随机场(MRF)来进行编码,即对于不同空间位置的噪音分布,我们对其噪音分布参数进行一个MRF建模,使其具有随空间变化的平滑性。

基于这样的想法,我们改造了之前所提的混合指数分布噪音建模的方法,具体想法就是,我们让空间的每个点具有自己的噪音分布形式,而同时用MRF对其分布参数进行约束。

基于这样的改造,我们的噪音建模方法对于数据沿空间heterogeneous的非iid噪音具有了一个更好的刻画能力,因而在包括高光谱图像去噪等多个问题上体现出更优的表现效果。这篇论文最终发表于2016年的TIP。

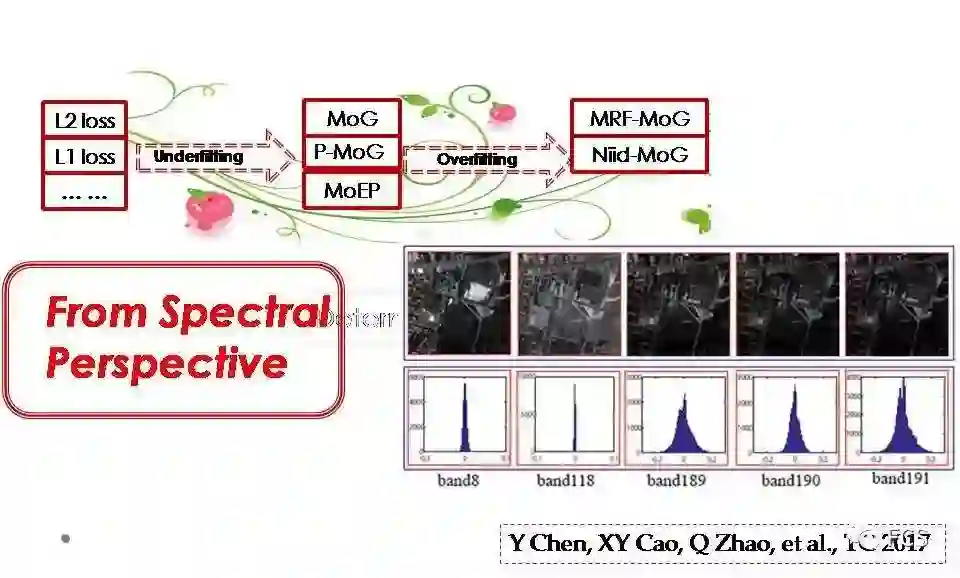
关于维度开放的非iid噪音,我们还是针对高光谱数据进行考虑的。实际上,当我们获得一个观测数据时,其不同维度的噪音往往存在差异,而传统使用简单误差函数的方式,其实是忽略了这种噪音的差异性。
比如对于高光谱图像而言,其沿不同谱段的图像,噪音是具有显著的不同的,有些谱段噪音相对小,而有些谱段噪音非常显著,很显然,其噪音是非iid的。但现有很多方法陷入了对误差函数固定的思维定势,实际上对此类噪音的编码是错误的。
基于对噪音维度开放性的非iid认识,我们尝试对高光谱图像的噪音提出三个理解:
每个谱段的噪音我们可以近似认为是一种iid的噪音分布;
不同谱段的噪音分布参数是不同的;
对不同谱段噪音分布参数加一个共轭先验,对其自由度进行约束和限制。

基于这三点理解,我们提出了这样一个概率模型。每个谱段的噪音我们建模为一个iid的混合高斯,而不同谱段的混合高斯参数不同,进一步用共轭先验将不同谱段噪音分布的参数关联起来。对应图模型中,红框内部就是对噪音建模的部分。
这个工作主要是我们小组陈阳博士等人共同完成的。

最终,在一些实际的高光谱图像数据中,这个方法的确取得了非常显著的去噪效果。可以从右下角的图观察到这个效果。我们的方法在有效去除噪音的同时,还可以做到对原图一些细节很好的恢复。这个论文最终是发表于今年的TC。

从时间开放性的角度来看,其实噪音也应该具有非iid特性。比如对于我们之前所说的视频前背景分离问题,有些视频帧前景目标显著,此时我们应该用一个厚尾分布,如拉普拉斯分布,对其噪音进行建模;而如果视频帧不包含显著的前景目标,我们就可以用一个简单的小方差高斯对其噪音进行建模;而更多的情况,视频前景包含非常复杂的噪音性态,此时我们就需要用更加复杂的噪音分布对其进行对应建模。
所以要对随时间不断变化的视频制定一个前背景分离的策略,我们需要考虑更为准确的噪音建模方案,即让我们的方法能够针对每一个视频帧,针对性的自适应学出特定的误差函数。
这种学习方式实际上对应于一种在线模式,即来一张或几张视频帧,应该马上让方法自动得出对其噪音/误差建模的最佳方案。
从这个角度来看,如果能够针对监控视频设计合理的在线前背景分离的方案,不仅可以像传统在线方法一样,加快方法计算的速度,而且有希望使得算法相对已有固定误差函数的方法表现更加的鲁棒,即更准确的分离出前景背景。这是我们做这个问题的一个基本动机。

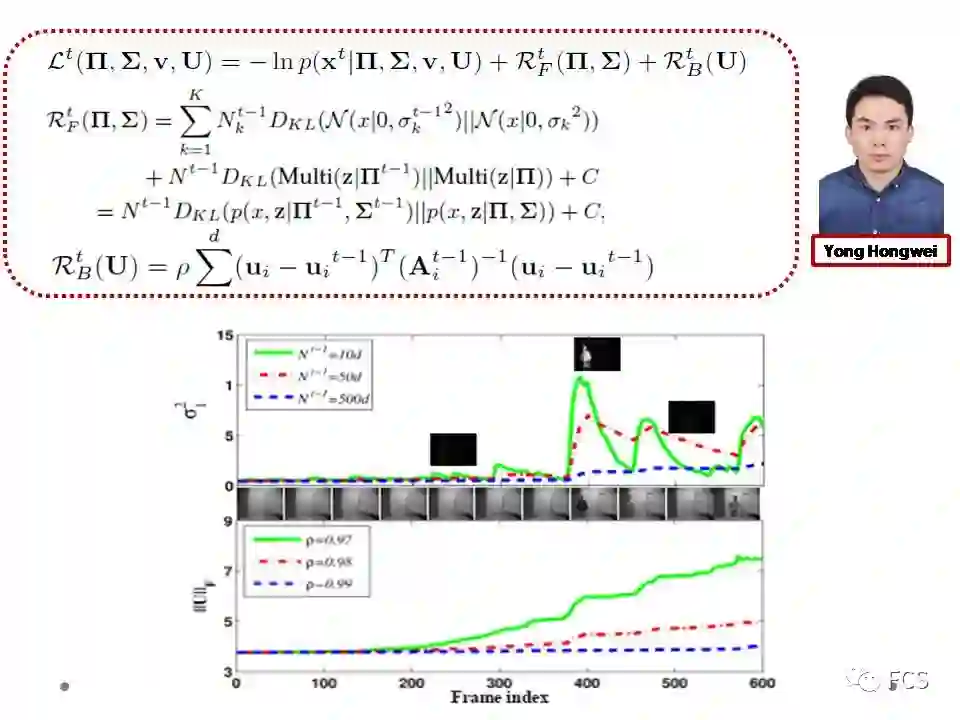
针对这一问题,我们构造了以下的模型。模型中主要包含三项:
对每个视频帧的似然项,即误差函数项,其作用在于对于每一帧图片尽可能准确的拟合其噪音形态;
对于噪音分布(随机性信息)参数的正则项,其作用在于让之前学习的噪音参数信息对当前帧的噪音参数进行抑制;
对于子空间参数(确定性信息)的正则项,其作用在于让之前学习得到的子空间参数对当前帧子空间参数进行抑制。
注意到,对于随机性信息抑制使用的正则项采用的是KL散度的形式,这体现了随机信息正则和确定信息正则的不同。
这个模型最大的特点在于,其可以针对每一帧视频,自适应的学习出一个对应的似然/误差函数。也就是说,随着时间的变化,每帧图片会自动的获得对应于其自身噪音特点的特有误差函数形式。
我们也期待这种对数据噪音的高度自适应性,能够带来其对实际视频前背景分离表现的鲁棒性。
这个工作,主要是我的硕士生雍宏巍完成的。这个工作花费了我们快三年的时间,最终终于做的较为完善并得到较好的实验效果。

为了使得方法能够自适应于实际监控视频发生的平移、旋转、尺度等变化,我们在模型中嵌入了一个仿射变换因子的变量,让其和噪音参数和子空间参数等一同进行学习。

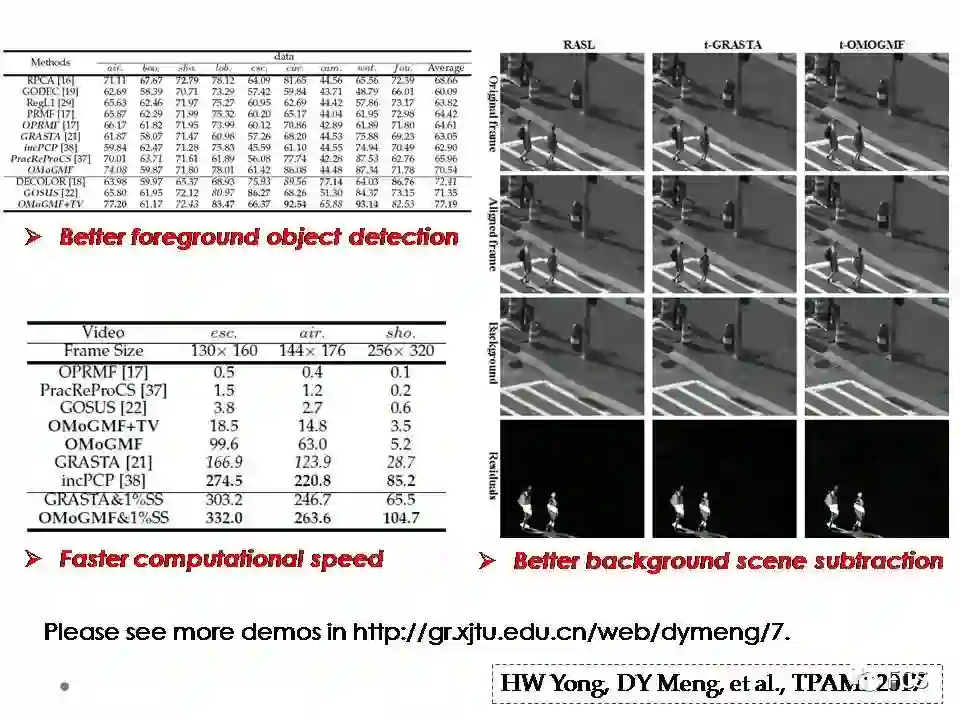
这个方法最终的效果还是让我们比较满意。
一方面,该方法可以很好的分离出视频的前景和背景。其中前景目标分离的精度可以用F-measure这个指标来量化度量。基于这个量化指标,我们的方法不仅表现比在线方法的效果好,其表现也超越了离线的batch-mode的方法。这充分体现了对于视频中随时间变化而呈现非iid特性噪音建模而带来的方法鲁棒性。
另一方面,通过采用下采样的技术,我们的方法平均计算速度达到了超过250帧/秒。这一速度也达到了视频处理的实时需求。
这篇论文接收在今年的TPAMI上,我们也已经在我的主页上公布了方法的代码。

可以注意到,以上所建模的噪音,从iid到非iid,从不加正则到加入噪音各种正则信息,噪音建模方法对于噪音的刻画,逐渐展现出与领域知识与结构相关的特点。
但之前使用的正则还是较为一般性的噪音正则信息,当面临特定领域具有特殊结构的噪音时,也许我们更应该考虑的,是基于领域知识与数据(噪音)结构的更针对性,更细致化的噪音刻画,这也是个人认为误差建摸未来最有希望的研究方向。
事实上,我们的研究越来越多的发现,现实数据中混杂的所谓“噪音”,事实上往往具有非常丰富的结构信息和深刻的物理内涵。
因此,摒弃传统的简单误差函数设置,而去更深刻考虑噪音的领域结构特点,并将其编码并嵌入到机器学习模型中,也许更可能帮助克服机器学习针对特定应用的鲁棒性问题,帮助其更为准确的编码噪音,从而获得更加鲁棒的表现。
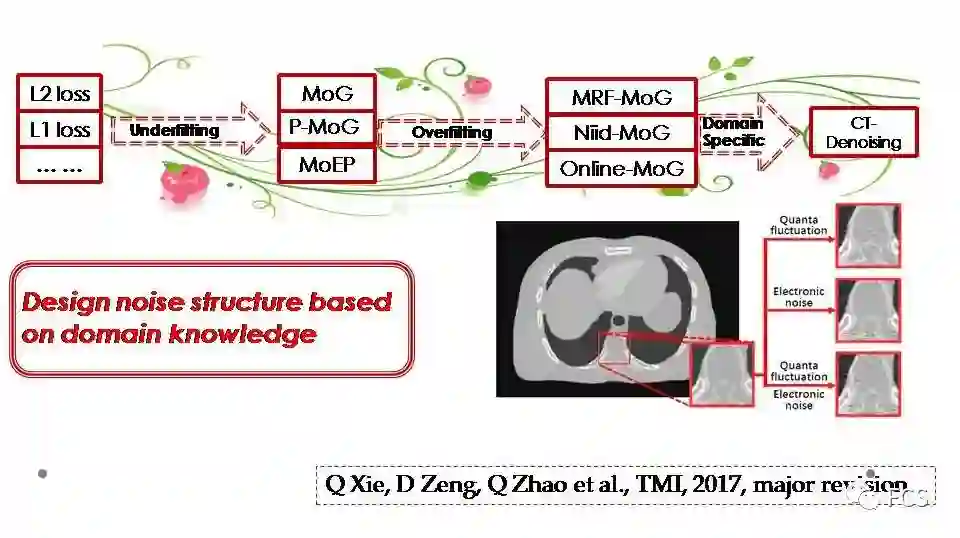
我们以CT图像去噪这一问题为例,简单谈一谈基于特定领域知识的噪音建模方法。

2015年底,南方医科大学的马建华教授来访我们小组,给我们介绍了CT图像去噪这一问题。
马老师针对这个问题做过长时间的研究,有很深入的思考,他们的方法也是当时这个问题的state-of-the-art。听完马老师的报告,我们接收到两个重要的信息。
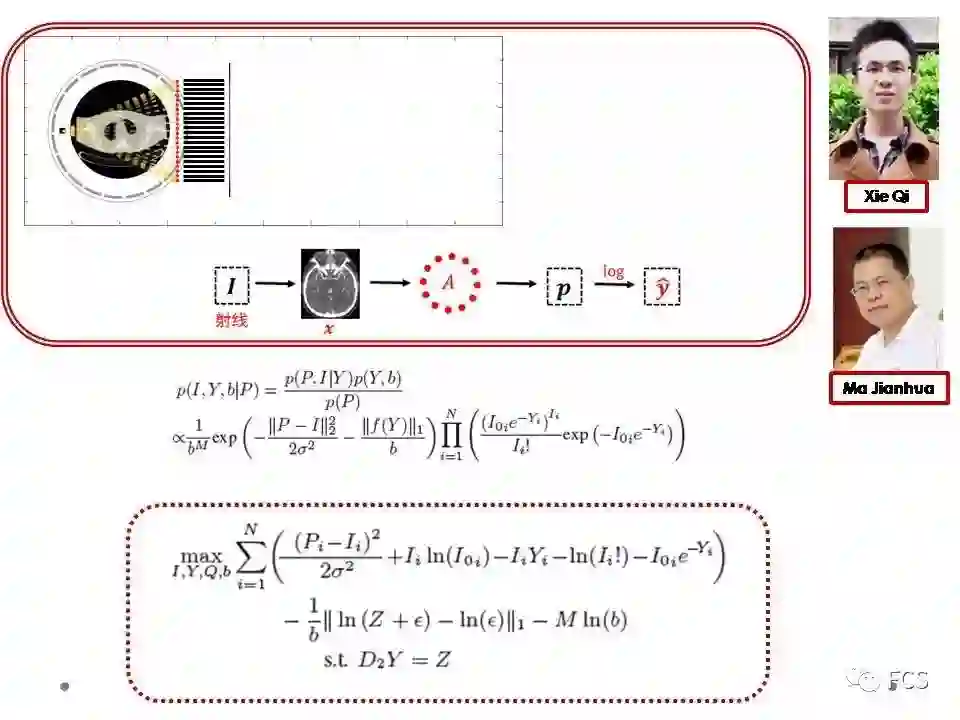
第一是CT图像的噪音和我们之前的噪音都有所不同,其机理比较复杂但又具有很强的领域知识。其图像(更准确的说是其通过设备采集到的投影图像)包含复杂非iid噪音结构。为了刻画这种非iid特性,马老师小组之前使用的方法是利用一个加权最小二乘方法来编码误差函数,而对应于每个点的误差权值各有不同,需要根据噪音实际的非iid特性来估计这个权值的大小。我们讨论发现,就是这个不同的权值,隐含体现的就是噪音的非iid性,如果我们能更为准确的刻画噪音,就能摆脱对传统设定固定误差函数的思维定势,可以让权值估计等问题得到自然的解决。
而我们得到的第二的信息是,CT投影图像的噪音的物理机制,是可以近似描述清楚的,也可以通过概率的方式来进行编码。其混入的噪音主要包含两种类型,一种是加性的电噪音,可以近似用一个高斯来拟合,另一个叫做量子波动噪音,是由于光子成像机理导致的,是一个近似的泊松乘性噪音。这两种噪音实际上我们可以用一个概率模型,统一的考虑在我们的误差函数之中。最终形成的误差函数看上去也较为奇特,但其每项都是有对应的物理含义的。

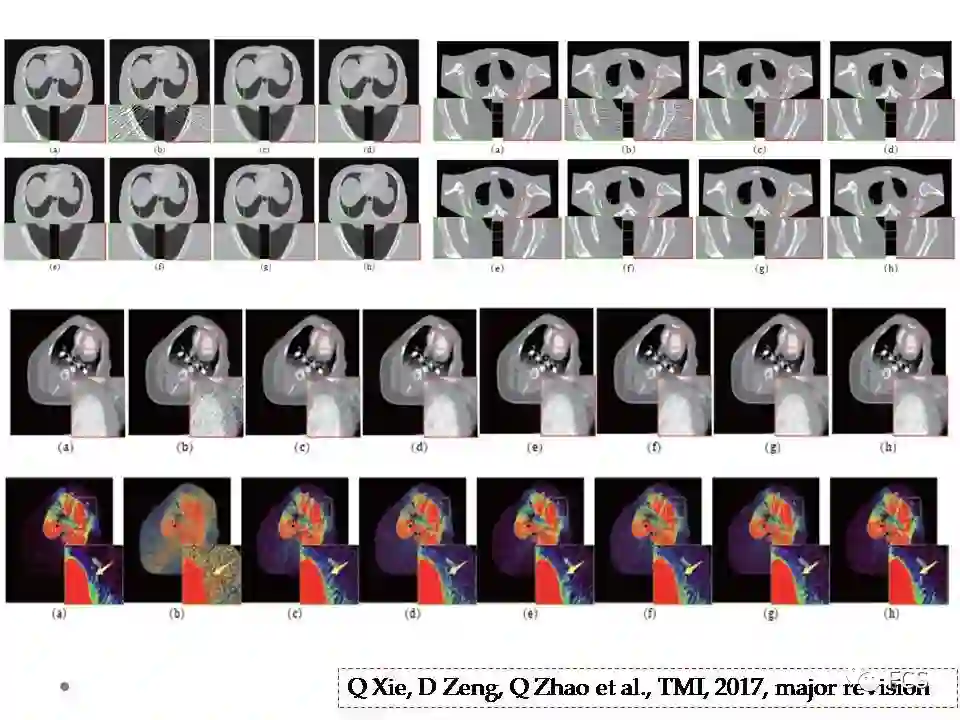
最终我们的方法也的确在一些人工和实际CT图像上得到了很好的去噪效果。这个论文投稿到了TMI,目前是第一审修改的状态。该工作主要是我们小组的谢琦博士,赵谦老师等成员和马老师小组共同合作完成的。

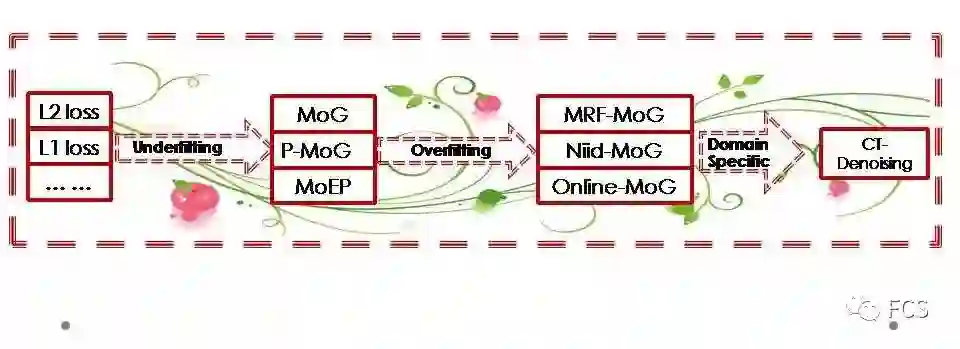
总体说来,这就是我们小组在误差建模这个方向上所做的一些研究尝试。
开始我们注意到传统固定误差函数的做法可能会欠拟合实际数据的复杂噪音而出现鲁棒性问题,因而开始尝试构建更为复杂的混合噪音分布模型。
而之后我们发现当我们不限制混合成分的数目而让噪音分布较为复杂时,可能会出现对于实际噪音过度拟合的问题,因而开始基于分而治之的思想考虑对数据噪音加入各种时、空、维的先验信息,而让其在局部产生更多的非iid噪音分布差异和变化。
而最近我们的研究越来越多的发现,针对特定领域针对性的噪音建模,通过对领域噪音更为准确的刻画,可能能够带来更好的去噪性能,并有希望进一步延伸到更多应用目标中。

这是我们在噪音建模方向发表的一些文章,已发表的文章我们基本都公布了相应的代码。
另外,我去年暑假在人工智能学会通讯上写了一个有关噪音建模原理的简单的介绍性文章,尽管现在看来里面还有不少认识不到位,理解不深刻的描述,但应该还是一个比较合适的科普材料。

感谢我们所有的小组成员,为了获得这些研究结果,他们付出了非常艰辛的努力,感谢我们所有的合作者,感谢徐宗本院士的支持与指导!
Frontiers of Computer Science

长按二维码关注Frontiers of Computer Science公众号
本内容为 Frontiers of Computer Science 公众号独家稿件,未经授权不得转载。授权合作请留言联系。