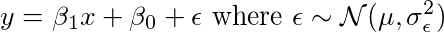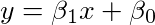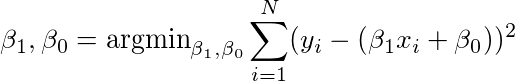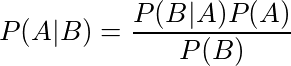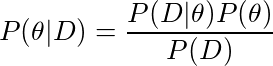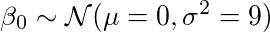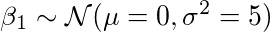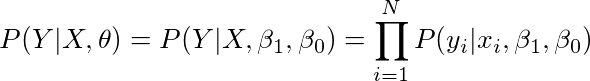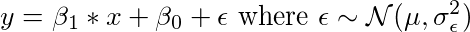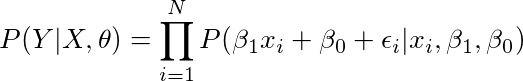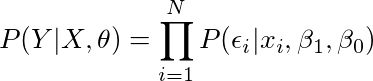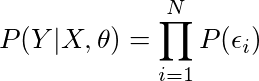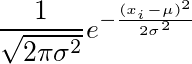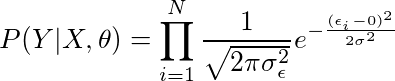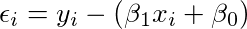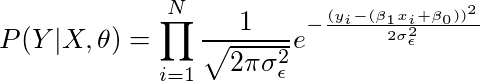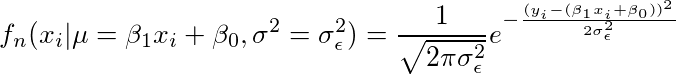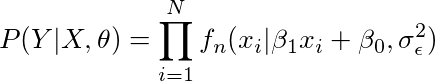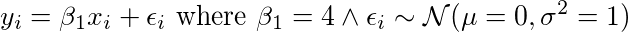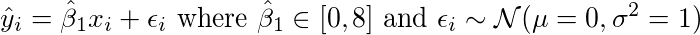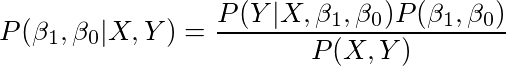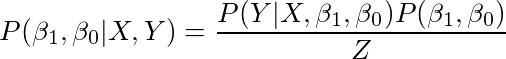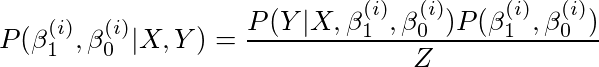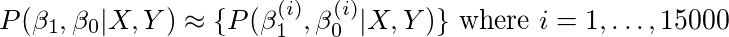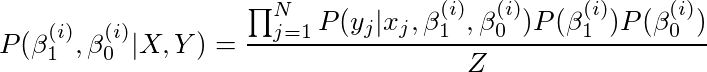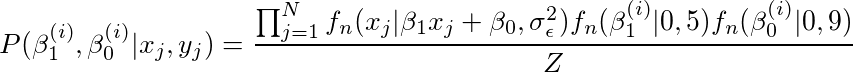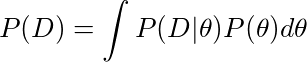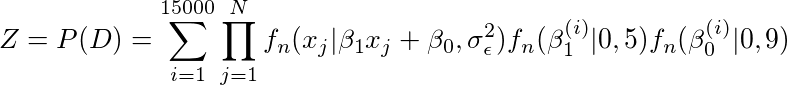解开贝叶斯黑暗魔法：通俗理解贝叶斯线性回归

【导读】本文是悉尼大学博士生 Thushan Ganegedara 撰写的一篇博文，主要介绍贝叶斯线性回归的内在原理。我们知道，深度学习可以利用大规模数据产生很好的结果，但是对于小样本高维度问题，贝叶斯是一种很好的学习方法。本文讲解了如何用贝叶斯解决回归问题，首先介绍了相关术语（先验、似然、后验）和相应的公式，并详细介绍了如何计算似然，文中通过实例辅助理解，内容比较详细适合初学者入门！

Unravelling Bayesian Dark Magic: Non-Bayesianist Implementing Bayesian Regression

解开贝叶斯黑暗魔法：非贝叶斯主义者实现贝叶斯回归

首先，我是一个学深度学习的人，直到最近我一直对深度学习很感兴趣。但我最近成了小样本高维度问题的受害者！所以我不得不转向那些善于“从小样本进行学习”的算法（“learning from little”）。

这对我来说是一个突然的变化。因为我已经远离贝叶斯“这种东西”很久了。但用到的时候必须做一些改变。所以我不得不从头开始学习（几乎）。我受到了先验概率，后验概率，KL-Divergence，Evidence Lower Bound（ELBO）等术语的轰击。然后我意识到“嘿，这与常用算法没有什么不同”。

我们将从一个频率型回归的例子开始。然后，我们将看到为什么我们想用一些更有前景的技术来解决我们的例子，如贝叶斯线性回归。之后，我们将陈述贝叶斯规则，然后介绍如何采用贝叶斯规则为给定数据找到一个好的模型。有了这个，我们可以定义先验，似然和后验术语（我的意思是定义，不是理解）。然后，我们将在漫长的学习道路上讨论这些术语（学习过程很长，但非常有启发性）。当我们讨论这些术语时，我们会举一些例子来让大家更明白其含义。最后，我们将通过比较我们开始的（先验）和我们发现的最好的（后验）对其做一个评估。

我们想解决的问题：Y =β1X +β0+ε

---

---

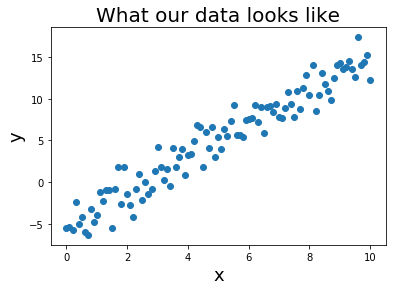
关于线性回归的第一个假设是，我们假设数据具有以下形式。

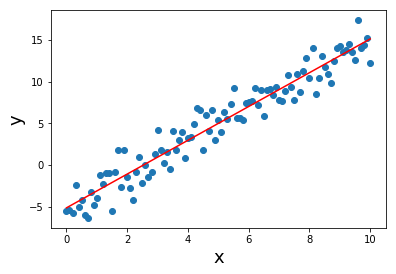
从这样的模型生成的数据如下所示。

普通最小二乘法（OLS）线性回归

---

---

说我们有这个数据集，我们需要一条合适的线。 我们通过如下公式来解决问题。

我们的目标是找到β1和β0，使得我们具有数据的最小RMSE（均方根误差）。 这在数学上，

首先让我们用线性回归拟合一条简单的线。

那么，这个结果说明什么？

它看起来不错。 实际上几乎是正确的。 但是，我真的可以依靠线性回归对有限的数据给出的答案吗？ 我不这么认为。 我想要一个通用的度量：

嘿，我之前看过很多这方面的数据，所以我对我的预测很有信心。

或者

呃，这一点在某处我没有看到太多数据。 答案可能是这样，但我不太确定。

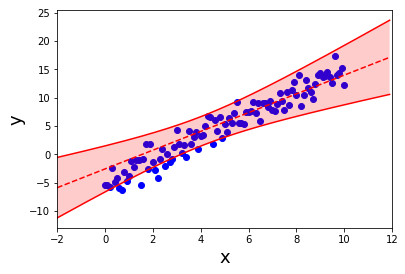
在没有数据的地方，你可以看到置信界限（conbdence bounds）如何增加（因此答案的不确定性增加）。 但线性回归不能给你这个。 这就是为什么我们需要贝叶斯线性回归。 那么我们如何使用高级的“贝叶斯”来解决这个问题呢？

 

贝叶斯规则

---

---

 

事件B发生条件下事件A发生的概率（后验 - 你感兴趣但不知道的事情）由下式给出：在A的条件下事件B发生的概率（可能性）乘以A发生的概率（先验）。

贝叶斯定理如何与这个问题相关？

这个公式我们已经听到了这一百万次！ 我想知道的是，这与机器学习有何关系。 为此，设A是用θ表示的学习模型（即β0和β1）的参数，B是你的数据D。现在让我们解释贝叶斯规则中的每个变量。

为了解决这个问题，我们将在给定数据的情况下得到θ（β0和β1）中所有参数的联合分布。这是我们需要的。换句话说，P（θ| D）告诉我们给定数据β0= 0.5和β1= 2.0，概率为0.5；β0= 1.5，β1= 3.0，概率为0.1。我们知道β0= 1.5 β1= 3.0这两个取值并不完全排除！这被称为后验分布。

我们通过下面步骤来计算：

• P（D |θ）：如果我们的模型中有参数θ，对观测数据的拟合情况

• P（θ）：我们之前对θ参数可能位于何处的先验设想。先验越接近真实，那么能越快越准地发现正确的后验分布。

• P（D）：这是一个常数值，代表观测数据的概率

先验P（θ）：我们认为参数是怎么样的？

---

---

 

我们需要从一些参数值开始吗？而在贝叶斯设置中，您不用一个值来指定某些值，而是用分布（例如高斯/正态分布）来表示。在我们的例子中，我们可以说，

用概率分布指定参数

我相信参数β0可以用均值为0和标准差为3的正态分布表示。也就是说，

β1也一样，

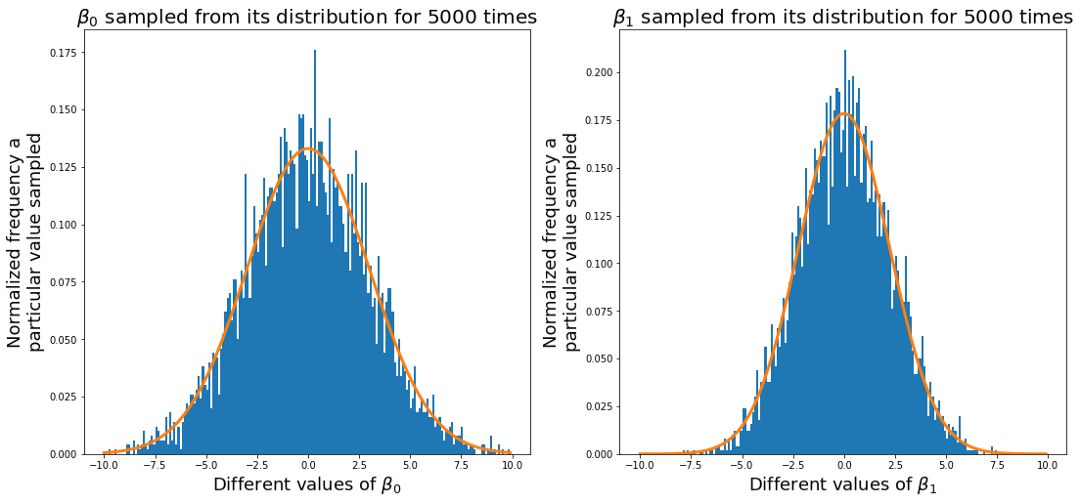
如果我们对β的许多值进行取样，我们会更接近真正的正态分布。 正如您对β0和β1所看到的，很多采样值接近0，,但β1与β0相比形状更加扁（β0与β1相比接近0的比例较低）

为什么是正态分布？

为什么我们使用正态分布？正态分布具有非常好的分析特性。因此，我们对后验分布的均值和方差有一个解决方法。有关分析后验解决方案的更多细节，请参见。

https://en.wikipedia.org/wiki/Bayesian_linear_regression#Posterior_distribution

 

为什么好的先验（P（θ））如此重要？

因为你必须依赖好的先验。也就是说，先验与后验越接近，你会更快得到真正的后验。如果你取的先验分布和后验分布一致，那么当你从先验分布中抽样时，你实际上是从后验中取样（这是我们需要的）。

现在转到下一个重要位置;看一下数据的可能性（即似然likelihood）

似然P（D |θ）：给定参数θ，模型对观测数据的拟合能力

---

---

 

我们如何计算给定参数集的数据似然。换句话说，我们要计算，

P（Y | X，θ）

下面，我们将逐步探索，找到一个方程，我们可以为每一项计算一个值。

计算似然：P（Y | X，θ）

1. 根据单个数据样本（y和x）的生成过程写出整个数据集（Y，X）的似然函数

现在让我们尝试为上述术语写出一个公式。

这个公式有下列假设，

• 数据点（xi，yi）是i.i.d（independent and identically distributed独立同分布）

2. 用x，β1，β0和ε来表示y

现在让我们回顾一下我们的数据是什么样的，

我们可以将这个公式拟合到似然公式中去，

3. 使用条件变量来分离ε

我们给出了所有的x，β1，β0，所以我们可以将它们从等式中去除，

思考一下上面这个公式是如何得到的，原理很简单：如果我们需要计算P（A + B | B），其实这个公式和当变量B“给定”之后的P（A | B）是一样的。 换句话说，P（B | B）= 1，所以我们可以从P（A + B | B）的顶部去除变量B，化简成P（A | B），结果不受影响。

4. 假设：噪音与数据无关

现在我们接下来的重要假设，

• 噪音独立于数据

有下式，

 

5. 用概率密度函数（PDF）写出概率

请记住，我们的噪音是正态分布的，我们可以写出一个正态分布的概率密度函数（PDF）

 

6. 假设：零均值与常量方差噪声

在线性回归中，我们对这个噪音成分做了两个重要的假设。 也就是说，这是一种正态分布，

• 它是零均值

• 它有一个常量的方差

有了这两个假设，并将噪声值插入到我们的公式中，

 

并有，

 

7. 最终的似然方程

因此代入得：

简化表示

我们写成，

因此，

直观地：如果y =β1*x，通过似然公式如何得到β1？

在我们的例子中有两个参数。 所以为了简单起见，暂时忘掉β0。 根于下面公式我们产生很多y和x的数据：

现在我们尝试通过尝试一堆不同的参数β1值来进行近似，这会产生一个新的y值和

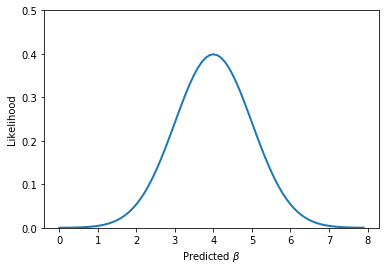
β1值的范围。 其似然函数P（y | x，β1）看起来如下。

由图可知，你可以看到，在β取4周围的值时，数据能够取得一个非常高的似然值。 这就是我们需要的参数。

更直观地：之前例子的似然

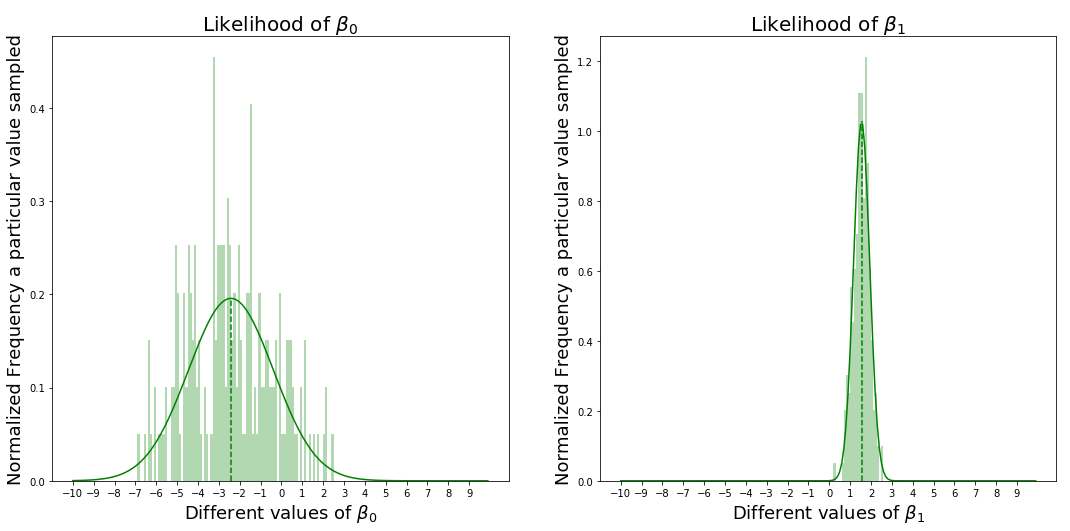
您可以将其推广到任何数量的β值（在本例中为β1和β0值）。 这是我们在例子中得到的图表。

上图说明什么？

上图显示，当β0接近-2.5，β1接近1.5时，我们可以看到数据X和Y能够得到最大的似然值，最好地拟合数据。还注意β1的似然是一个很大的针尖形状（spike），β0的形状更宽。 现在我们需要考虑每个变量对模型精度的影响。

后验P（θ| D）：我们最终需要什么？

---

---

假设您观察了您的数据，后验是参数（即β0和β1）的概率密度函数。 快速回顾一下，这是我们想要的最终结果（即贝叶斯规则的左侧）。 为了计算这一点，我们需要联合P（Y | X，β1，β0），P（β1，β0）和P（X，Y）进行计算，如下：

现在P（X，Y）是常量。因为只要数据不变，它也不会改变。 所以我打算用一个常量Z来重写P（X，Y）。我们将讨论如何计算这个Z。

换句话说，

后验仅仅是一个加权的先验，其中权重是给定参数值的数据的似然大写。

 

计算后验分布，有两种解决方法：

• 得到后验分布的解析解。

• 通过对后验分布进行采样，得到许多β1和β0的值，然后近似这个后验分布。

我们将要使用采样

我们感兴趣的是后验的行为与似然和先验的关系。我们通过抽样来计算。

因此，我们将用上面的公式来拟合抽样。

然后我们通过对β0和β1取15000个不同的值，从它们各自的先验值中抽取并计算每个β0和β1组合的可能性，来近似完整后验。 更具体地说，就我们的例子而言，

 

因此我们得到了，

 

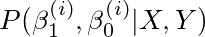
由于数据是独立同分布且β1和β0是独立的，我们可以将上面的式子写成，

通过符号简化，我们得到，

证据（Z = P（D））：使后验概率总和为1

---

---

Z = P（D）= P（X，Y）

P（D）—这有时称为证据，表示看到数据的概率。 由下式得到，

我们如何计算Z？

我们如何估算这个值？ 我们得到β1和β0样本的所有不同组合的P（D |β1，β0）P（β1，β0）（即贝叶斯规则公式右侧的顶部）的总和。 得到的样本越多，将能更真实地得到观测数据的概率。 更具体地说，我们可以这样计算Z，

 

这个公式没有什么可怕的，这只是重复添加P（β1（i），β0（i）| xj和j）的顶部部分一遍又一遍的总次数来取样不同的β1和β0。 Z起的是归一化的作用，所以后面的累加和就是1（这你是知道的，因为它是一个概率分布）。

先验，似然，后验，的一个例子

---

---

下面我们用一个例子展示先验，似然和后验。

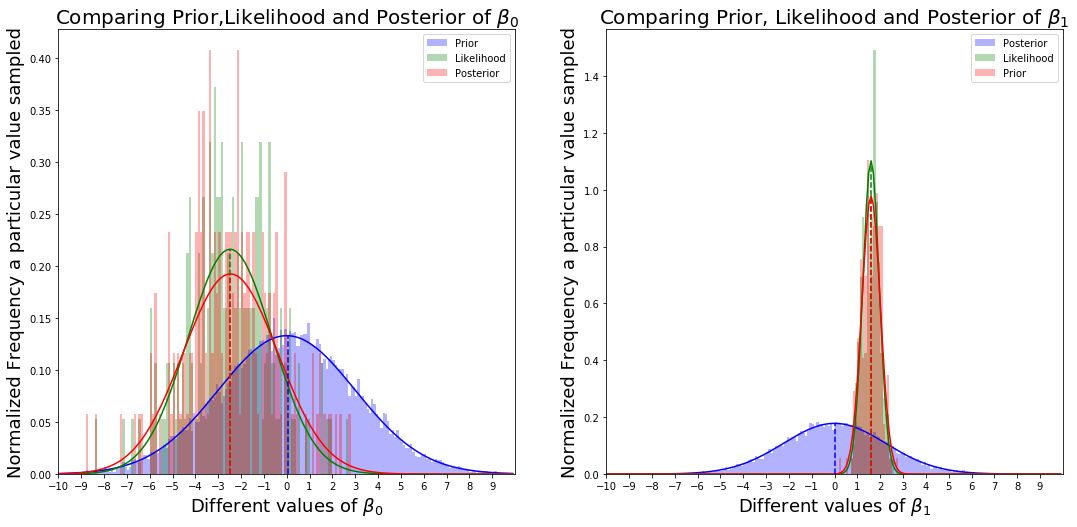
图表说什么？

我可以做出两个重要的观察。

• 你可以看到，由于我们的先验稍微偏离了真实的后验，因此似然概率实际上是把后验从先验拉开。 如果先验很接近真实的后验，你会看到这种拉力下降。

• 接下来的观察是，与β0相比，参数β1似乎更敏感。 否则，β1的变化比β0更会影响结果的准确性。

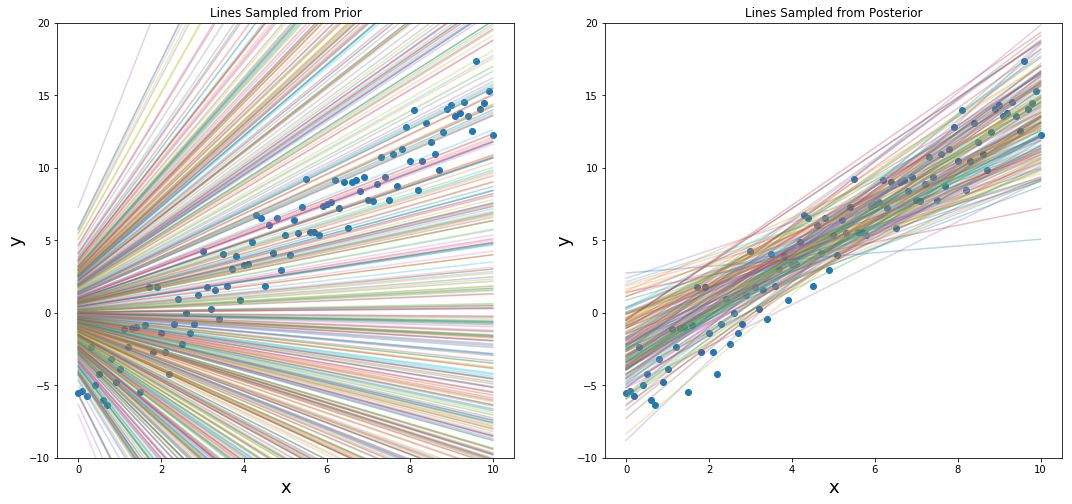
最后，我们做一个比较，以查看从先验分布（仅前500个样本）和后验分布中抽取的线的差异。 你可以判断哪个更好。

对于一个新的数据点，我们如何获得答案？

---

---

根据β1和β0，我们有一个很直接的后验分布。对于给定的x，你只要从后验分布中采样不同的β0和β1，并得到y的值（即Y =β0+β1x）。用这组潜在的候选项y，可以计算y的平均值和y的标准差。

Jupyter链接在这里：

https://github.com/thushv89/nlp_examples_thushv_dot_com/blob/master/bayesian_linear_regression.ipynb

总结

---

---

虽然内容有点长，但希望能够揭开贝叶斯方法所具有的某些“黑暗秘密”（“dark secrets”）的神秘色彩。通过示例，我们理解贝叶斯线性回归是如何工作的; Y =β1X +β0+ε。

我们首先看到频率主义方法解决了这个问题，但忽略了一些关键信息;答案的不确定性，但是我们看到贝叶斯方法不仅会给出最可能的答案，还会告诉我们这个答案的不确定程度。

参考文献：

https://towardsdatascience.com/unraveling-bayesian-dark-magic-non-bayesianist-implementing-bayesian-regression-e4336ef32e61

作者个人主页：www.thushv.com

-END-

专 · 知

人工智能领域主题知识资料查看获取：【专知荟萃】人工智能领域26个主题知识资料全集（入门/进阶/论文/综述/视频/专家等）

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！

请扫一扫如下二维码关注我们的公众号，获取人工智能的专业知识！

请加专知小助手微信（Rancho_Fang），加入专知主题人工智能群交流！

点击“阅读原文”，使用专知