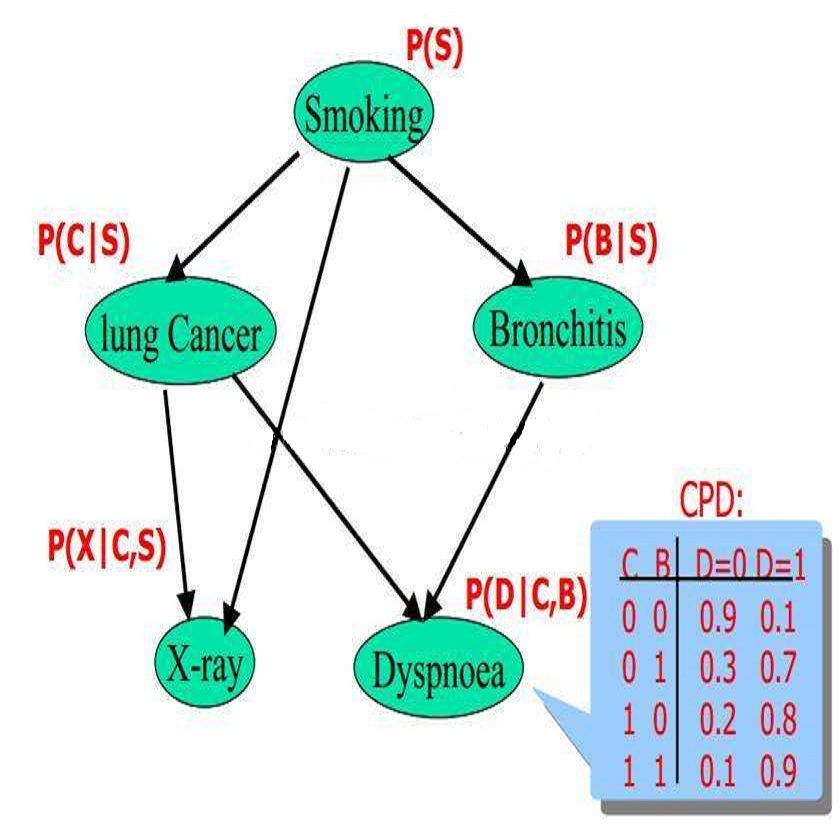
贝叶斯思想概述:从贝叶斯定理到贝叶斯网络
翻译 | AI科技大本营(ID:rgznai100)
参与 | 刘畅
假设世界上存在一种非常罕见的疾病,你患有这种疾病的几率只有千分之一。你想知道你是否被感染了,所以你做了一个99%准确的测试...且测试的结果是阳性的(译者注:阳性是感染了病毒的情况)! 那么你到底有多确定你真的被感染了?
怎么让疾病的第二次测试结果告诉你,你确实被感染了?
对于上述问题,如果你不想做所有的数学计算,而是更喜欢画一个网络结构来帮助自己更好地理解,那这篇文章是非常适合你的!
第一个测试
由于它是一种非常罕见的疾病(千分之一的机率被感染)。下表(称为条件概率表)给出了身体中有这个病毒的概率
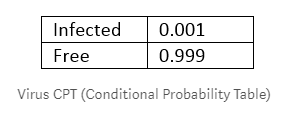
这个表格显示只有千分之一的人被感染了。也可以这样认为:一千人中有999个人都是没有被感染的。
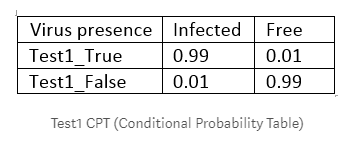
现在我们做了一个相似的测试表:第二个表表示测试的准确性。就是测试结果会告诉测试的准确度。因此,如果你被感染了,测试结果就是True,就是意味着你有99%的可能性被感染了,如果你没有被感染,测试结果将显示false(也是99%的准确度)。在这两种情况下,测试结果的错误率都是1%。
接下来的这张图显示,在给定测试结果的病毒是否存在的条件下,它的结果也取决于测试(如上面的表格所示):
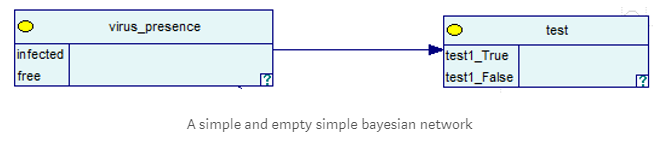
然后,当我提供证据证明测试结果是True。由于只做了一次测试且结果是阳性的,因此该网络告诉我病毒存在于你的身体里,但是实际上病毒存在的概率只有9%!
那为什么会这样呢?这个数字来自贝叶斯定理:
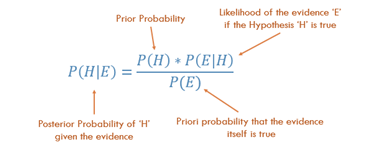
在这个问题上,计算方法如下:

所以,即使你做了一个99%准确的测试,但是患该病的几率也只有9%。
这个计算看起来很复杂,但是一旦在图中来表示,我们就可以更好地理解贝叶斯思想是如何工作的。
进行第二次测试:
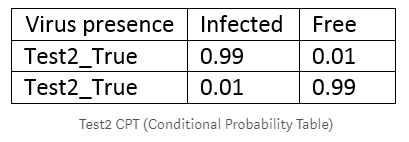
如果你进行第二次测试会发生什么?让我们假设这个新的测试也有99%的准确度,然后有一个和第一次测试一样的表:
相应的贝叶斯网络将是如下图所示:
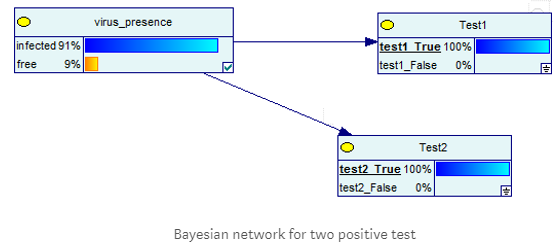
这意味着:如果进行了两个阳性的测试,患该病的几率增加到了91%。由于加上了上一次实验的结果,并且是连续的两次实验,患病的几率从9%跳到了91%。但并不是100%!
在另一种情况下,如果第二个测试是一个阴性样本,则有100%的几率没有该疾病。
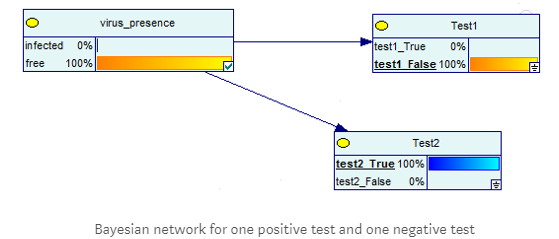
进行三次测试:
在三个测试中,所有的测试都有一样的准确度,我们可以看到一些有趣的结果。如果你有证据证明这3个测试结果都是阳性的,那么现在100%肯定你被病毒感染了。
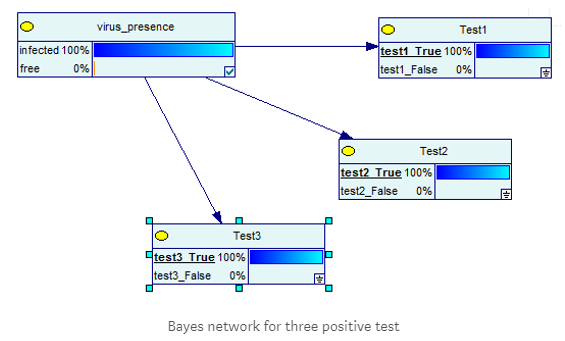
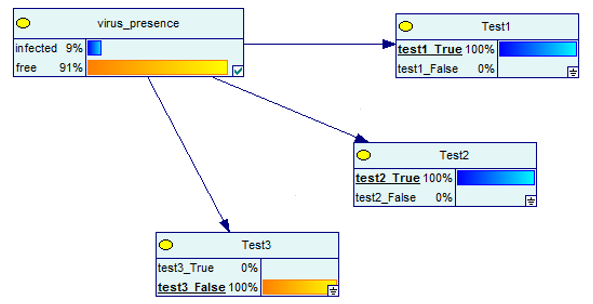
但是如果一个测试结果是false,之前的结果会再次出现,即病毒只有91%的机会存在于你的体内:
总之,贝叶斯网络有助于我们展现贝叶斯思维,当数据量适中、不完整和/或不确定时,贝叶斯网络可以用于数据科学中。他们还可以引入专家判断来建立或完善网络。它们允许“模拟”不同的场景,而且能够表示出输入值(在这个例子中即是病毒的存在和测试的准确度)与输出(事件实际发生的概率)是如何在某种程度上联系在一起的。
在这篇文章中,我解释了如何从贝叶斯定理开始建立贝叶斯网络。我目前正在研究贝叶斯网络来预测项目的成本和风险。我想分享构建这种强大的人工智能工具的基础知识。
在这个暖心的视频中也解释了这个例子:https://youtu.be/R13BD8qKeTg
了解更多关于贝叶斯网络的知识:
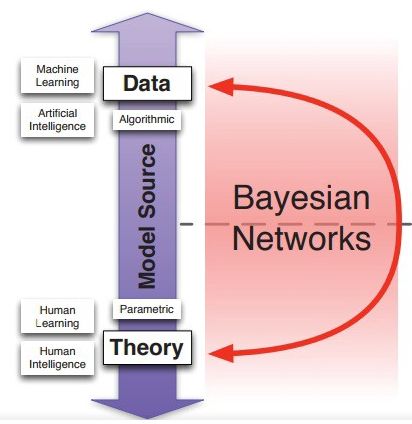
关于在模型源上如何进行理论与数据的横向划分,贝叶斯网络有其特殊性。贝叶斯网络可以建立在人类的知识上,即理论上,也可以从数据中学习。因此,他们可以使用整个光谱作为模型源。此外,由于其图形结构,基于机器学习的贝叶斯网络在视觉上可以解释,因此也促进了人类学习和理论的发展。
贝叶斯网络允许人类学习和机器学习同时进行,也就是说,贝叶斯网络可以由人类和人工智能相结合而发展起来。除了跨越理论和数据之间的界限外,贝叶斯网络还具有因果关系这种特殊性质。
在特定条件下,即特定的理论驱动假设下,贝叶斯网络可以促进因果关系的推理。事实上,贝叶斯网络模型可以涵盖从关联/相关(Association/Correlation)关系到因果关系的全部范围。
实际上,这意味着我们可以将因果假设加入到现有的非因果关系网络中,从而建立一个基于因果关系的贝叶斯网络。当我们试图模拟一个领域中的干预项,例如估计一个治疗的效果时,这一点尤其重要。在这种情况下,必须使用因果模型,而贝叶斯网络帮助我们实现了这种过渡。来源:Bayesia book
原文链接:
https://towardsdatascience.com/will-you-become-a-zombie-if-a-99-accuracy-test-result-positive-3da371f5134
热文精选
不用数学也能讲清贝叶斯理论的马尔可夫链蒙特卡洛方法?这篇文章做到了
盘点深度学习一年来在文本、语音和视觉等方向的进展,看强化学习如何无往而不利
干货 | AI 工程师必读,从实践的角度解析一名合格的AI工程师是怎样炼成的
AI校招程序员最高薪酬曝光!腾讯80万年薪领跑,还送北京户口
算法还是算力?周志华微博引爆深度学习的“鸡生蛋,蛋生鸡”问题