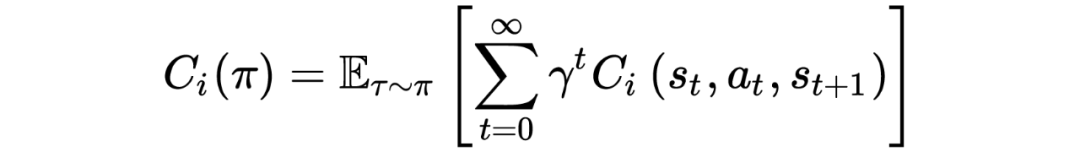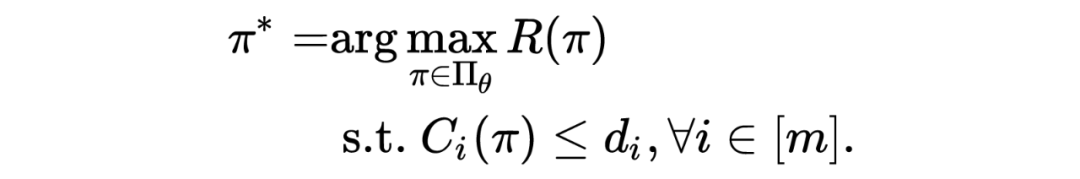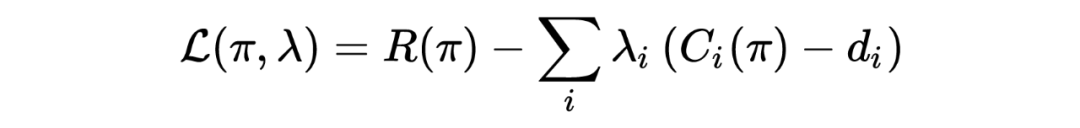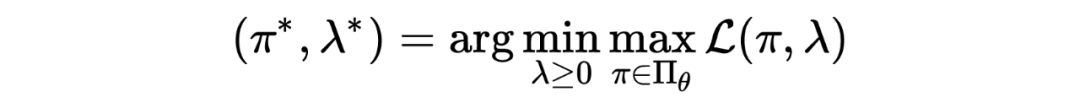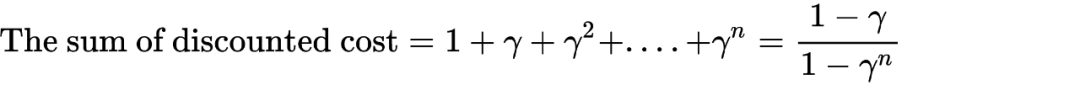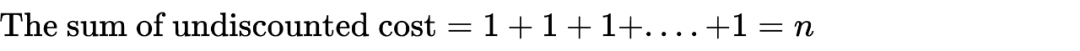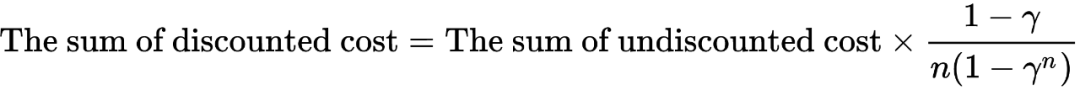针对安全探索的受限强化学习：原始对偶优化算法

会员服务 ·

针对安全探索的受限强化学习：原始对偶优化算法

2022 年 1 月 8 日 PaperWeekly

©作者 | 周宣含

学校 | 国防科技大学

研究方向 | 深度强化学习

在强化学习中，智能体通过在未知环境中探索与试错来学习如何决策。大多数 RL 算法允许智能体自由地探索环境，并采取任意能够提升奖励的动作，然而，能够获得较高奖励的动作同时也可能会带来较大风险。而在一些实际场景中，确保智能体的安全至关重要。

不同于标准 RL 只需要最大化奖励函数，此时智能体所采取的行为必须能够避免危险的情况，因此设计者需要合理地设计奖励函数，通过不同的权重系数（奖励因子与惩罚因子）在最大化奖励以及减少危险代价之间取得平衡。这其中存在着两个问题：

1）需要满足的约束条件与正确的权重参数之间不存在给定的映射关系，如果惩罚因子选取得过小，智能体可能会学习到危险的行为，相反，如果惩罚因子选取得过大，智能体可能无法学习到任何东西；2）对于给定的权重系数，即使能够让智能体最终学习到满足约束的最优策略，也依然无法保证智能体在整个训练过程中都能满足约束。

一种确保智能体安全性的方法是在标准马尔科夫框架中增加约束条件，把问题转变成受限马尔科夫决策过程（constraint Markov Decision Process，CMDP），此时智能体的目标是在满足 long-term 代价约束的条件下最大化 long-term 奖励。这种方法能够同时解决上述的两个问题。

当前求解 CMDP 的算法主要包含两大类：原始对偶优化（primal-dual optimization，PDO）算法与受限策略优化（constraint policy optimization，CPO）算法。其中，PDO 算法以拉格朗日松弛（Lagrangian relaxation）技术为基础，轮流更新原始域参数与对偶域参数。具体来说，原始策略参数利用策略梯度上升的方法进行更新，而对偶域的参数则采用对偶梯度上升的方法进行更新。

CPO 与 PPO 的区别在于对偶域的更新方式，在 CPO 中，每一次迭代都会通过求解一个精心设计的优化问题来直接求解对偶参数，这样确保了训练过程中约束条件也能够得到满足，CPO 是 TRPO 在 CMDP 中的扩展。open AI 在对于 safety RL 的 benchmark 中提到，CPO 的实际效果不如 PDO，并且 CPO 的算法框架基于 TRPO 算法，而 PDO 可以应用在各种标准 RL 算法中，因此这里只介绍 PDO 算法。

Constraint RL

1.1 受限马尔科夫决策过程（CMDP）

CDMP 在 MDP 的基础上增加了对于长远折扣代价（long-term discounted costs）的约束。具体来说，假设总共有个代价函数，其中每个代价函数表示状态-动作对到代价之间的映射关系。类似于奖励收益，策略下的长远折扣代价收益被定义为

对应的约束门限值为。CMDP 的目标是在满足长远代价收益的情况下最大化奖励收益，即

除此之外，约束条件还有多种形式，例如机会约束，风险条件价值约束（constraints on the conditional value at risk，与最坏情况结果的一小部分相比的预期代价总和），每个状态的独立约束。实际上，在 Sutton 的书中提到过，所有的目标与目的都可以用奖励函数来表示，因此通过合理设计代价函数所能表示出来的约束条件种类是十分广泛的。

另外，Constraint RL 与 multi-objective RL 十分相近，但是两者有着一定的区别，在 constraint RL 中，当约束条件得到满足时，通常存在一个饱和点（saturation point），当到达该点时，继续减少代价函数的值就不再具有任何意义，这个点对应的代价函数的值也就是约束条件的门限值，这个门限值在 multi-objective RL 中不存在类似的定义。

1.2 原始对偶优化（primal-dual optimization）

为了求解 CMDP，可以采用拉格朗日松弛技术，具体来说，上述 CMDP 问题的拉格朗日函数为

其中是拉格朗日因子。原带约束的优化问题可以转换为如下不带约束的优化问题：

为了求解这个不含约束的 minmax 问题，标准的方法是采用迭代原始-对偶方法，即在每一次迭代中轮流更新原始策略与对偶变量。在第次迭代中的原始-对偶更新过程如下：

固定，执行策略梯度上升：，其中表示更新步长。这里的策略梯度既可以是 on-policy 的似然比策略梯度（REINFORCE 与 TRPO等），也可以是 off-policy 的确定性策略梯度（例如 DDPG）。
固定，执行对偶更新：。CMDP 中不同方法的区别就在于对偶更新函数的选择。例如，PDO 采用简单的对偶梯度上升，其中是步长，是对于对偶空间的投影。相反，CPO 通过在每一次迭代中构建新的优化问题来求解对偶变量，进一步加强了约束。

实际算法举例

2.1 Primal-Dual DDPG for CMDPs

这里提供 DDPG 算法的原始-对偶优化版本用于求解 CMDP，该算法中的原始策略更新与对偶变量更新均利用经验回访池中的 off-policy 数据样本。为了方便描述，假设此时 CMDP中只存在 1 个约束，多个约束的情况也可以轻易地扩展得到。在原始-对偶 DDPG 算法中，存在以下几个神经网络：

Reward critic Q-network 以及 reward target critic Q-network ；
Cost critic critic Q-network 以及 cost target critic Q-network ；
Actor policy network 以及 actor target policy network ；

具体算法如下：

可以看出，这里的算法与标准 DDPG 的算法区别在于：

1. 多了 1 个用于表征长远折扣代价的神经网络；

2. 需对对偶域的拉格朗日因子即惩罚因子进行梯度上升。

类似的，PDO 还可以应用在 TRPO、PPO、TD3、SAC 等算法上。

2.2 存在的问题

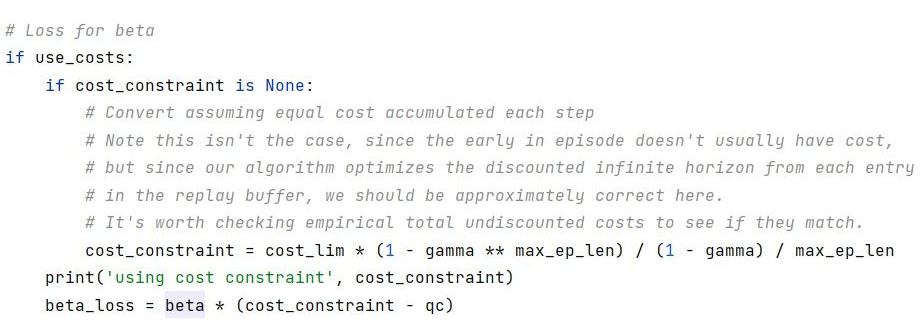
在实验中我发现这种方法存在一定的问题，在实际场景中我们的约束条件是有一定物理意义的，例如一段时间内机器人的能量消耗必须小于一定的阈值，保证机器人的正常运作，这里的阈值是根据无折扣的代价之和求得的，但是在上面的算法流程中，利用了一个神经网络去拟合代价对应的 Q 值，这里的 Q 值对应的是有折扣的代价收益，与奖励对应的收益类似，因此这里的代价 Q 值和我们实际中的代价之和是有区别的。在 open AI 提供的实验中，代价比较简单，通常为 1，此时 open AI 的代码在假设每个 step 都有代价，且均为 1 的情况下，利用有折扣代价之和与无折扣代价之和之间的等式关系：

将实际无折扣代价之和得到的门限值转换成了有折扣代价之和得到的门限值：

这种方法基于每个时刻均有代价，且代价值固定的假设，在实际场景中，代价值和奖励值一样，可能存在各种各样的取值，并且不是每个 step 都会存在，所以这种等式变换是十分不精确的，并不适合实际场景。因此，在我个人的实验中，并没有采用神经网络对代价对应的收益进行拟合，而是直接采用 on-policy 的数据计算一个 episode 的代价之和做为代价收益，然后利用这个值对拉格朗日因子进行梯度更新。

参考文献

[1] A. Ray, J. Achiam, and D. Amodei, ‘Benchmarking Safe Exploration in Deep Reinforcement Learning’, p. 25.
[2] Q. Liang, F. Que, and E. Modiano, ‘Accelerated Primal-Dual Policy Optimization for Safe Reinforcement Learning’, arXiv:1802.06480 [cs, stat], Feb. 2018, Accessed: Apr. 14, 2021. [Online]. Available: arxiv.org/abs/1802.0648
[3]J. Achiam, D. Held, A. Tamar, and P. Abbeel, ‘Constrained Policy Optimization’, arXiv:1705.10528 [cs], May 2017, Accessed: Apr. 17, 2021. [Online]. Available: arxiv.org/abs/1705.1052
[4]Y. Chow, M. Ghavamzadeh, L. Janson, and M. Pavone, ‘Risk-Constrained Reinforcement Learning with Percentile Risk Criteria’, arXiv:1512.01629 [cs, math], Apr. 2017, Accessed: Apr. 17, 2021. [Online]. Available: arxiv.org/abs/1512.0162

特别鸣谢

感谢 TCCI 天桥脑科学研究院对于 PaperWeekly 的支持。TCCI 关注大脑探知、大脑功能和大脑健康。

更多阅读