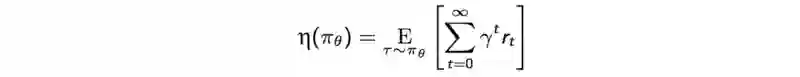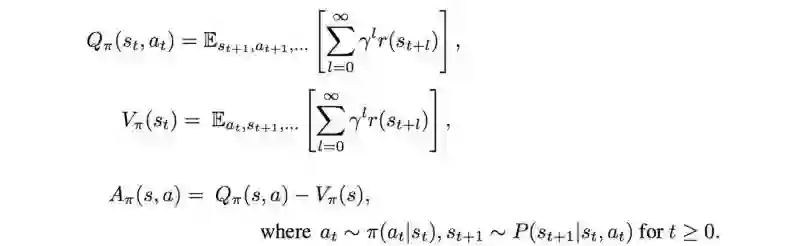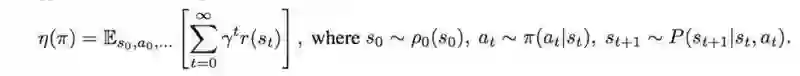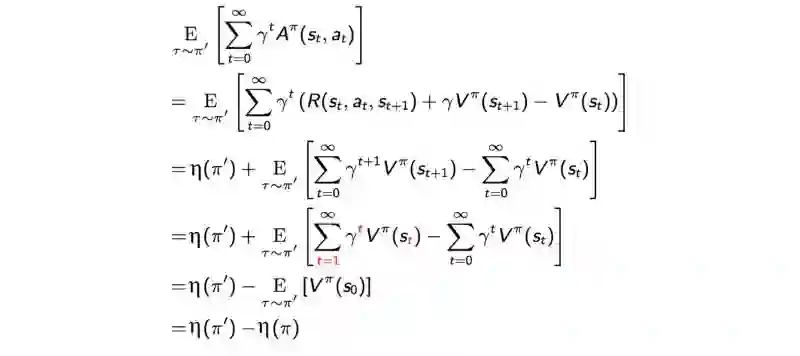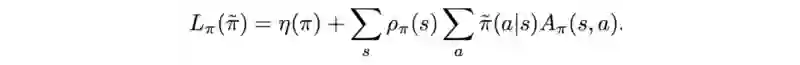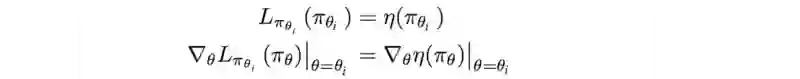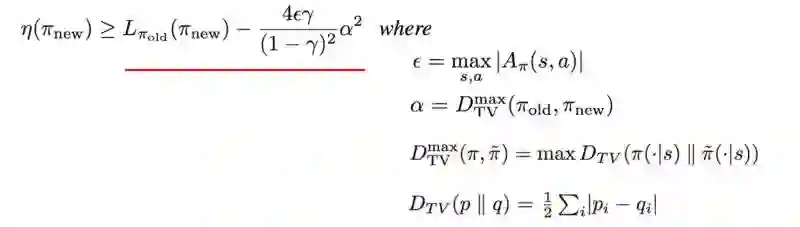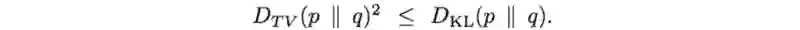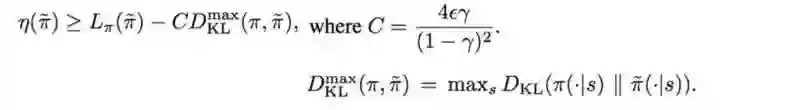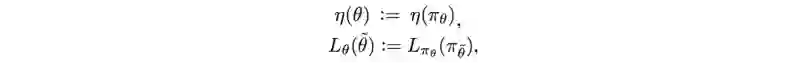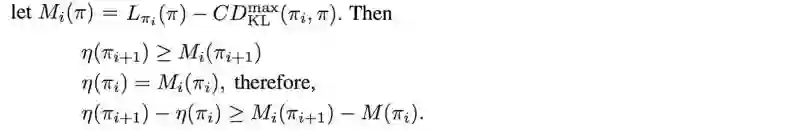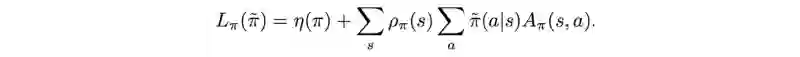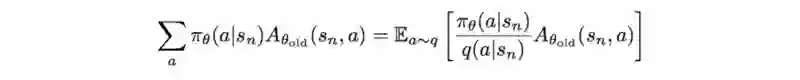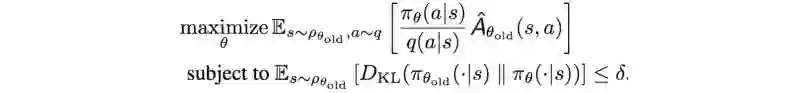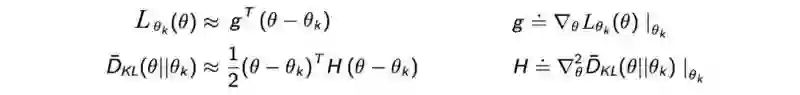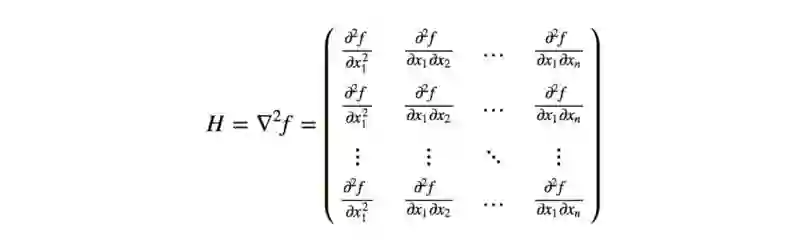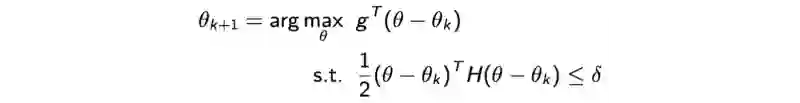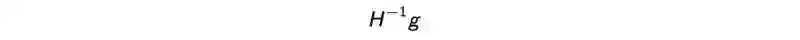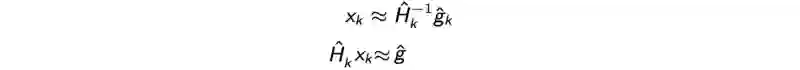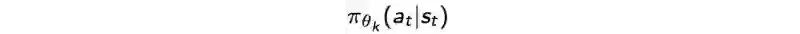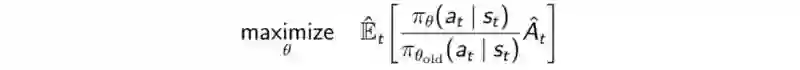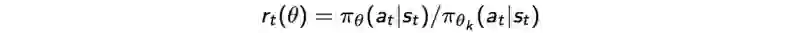腊月廿八 | 强化学习-TRPO和PPO背后的数学

本文为 AI 研习社编译的技术博客，原标题 ：

RL — The Math behind TRPO & PPO

作者 | Jonathan Hui

翻译 | 斯蒂芬•二狗子、贝琳达•霍尔

校对 | 斯蒂芬•二狗子     审核 | 邓普斯•杰弗      整理 | 菠萝妹

原文链接：

https://medium.com/@jonathan_hui/rl-the-math-behind-trpo-ppo-d12f6c745f33

注：本文的相关链接请点击文末【阅读原文】进行访问

强化学习-TRPO和PPO背后的数学

照片来源于 Nigel Tadyanehondo

TRPO 算法 (Trust Region Policy Optimization)和PPO 算法 (Proximal Policy Optimization)都属于MM(Minorize-Maximizatio)算法。在本文中，我们将介绍基础的MM算法，并且通过几个步骤推导出TRPO和PPO的目标函数。在我们的强化学习系列课程之中( Reinforcement Learning series )，我们将会分别学习不同的主题的内容。但是在本文之中，我们将会展示更多的数学细节给这些好奇的、想了解这些目标函数背后原因的读者们。

  Surrogate function(替代函数)

RL( Reinforcement Learning即强化学习) 的目标就是最大化预期折扣奖励(the expected discounted rewards)。下图之中，红色的线表示期望折扣回，其中 η 被定义为：

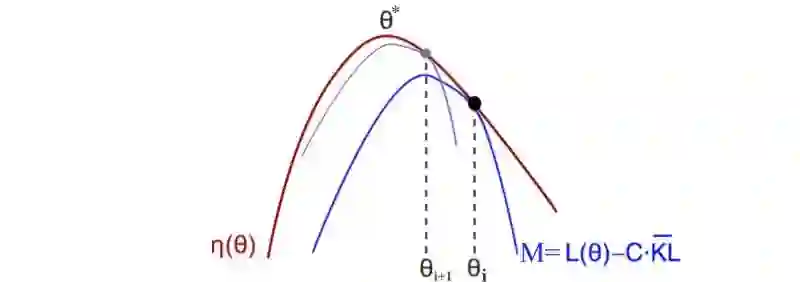
 Modified from source

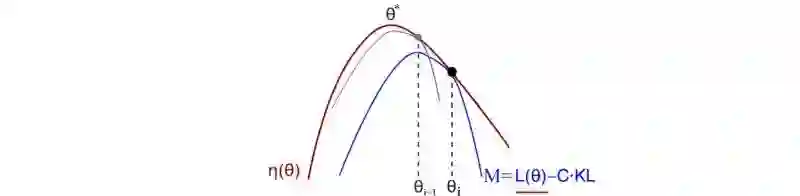
MM是一种迭代方法，对于每次迭代，我们发现替代函数M(蓝线)有如下性质：       

• 是η的下界函数

• 可用于估计当前策略的 折扣奖励 η

• 易于优化(我们将会把替代函数近似估计为一个二次方程)

在每一次迭代之中，我们找到最佳的M点并且把它作为当前的策略。

之后，我们重新评估新策略的下界并且重复迭代。当我们持续这个过程，策略也会不断的改进。因为可能的策略是有限的，所以我们当前的概率最终将会收敛到局部或者全部最优的策略。

  目标函数

如下所示，有原始的策略梯度PG、置信域策略梯度TRPO和近端策略优化PPO版本的目标函数。接下来我们将详细进行证明。

简而言之，我们想最大化优势函数：动作值函数（奖励的最大期望）减去对应状态拥有的基准值。约束条件为新旧策略的差异不能过大。本文余下部分将数学证明该约束问题。

值函数、动作值函数和优势函数的表达式

首先，我们先定义Q值函数、状态值函数和优势函数。直接书写如下：

折扣奖励函数

折扣奖励η的期望计算如下：

或者，我们可以使用其他策略计算策略的奖励。以便比较两种政策。

证明：

𝓛 函数

接下来，使用MM算法找到当前策略下近似η下界局部值的函数 。让我们将函数 𝓛 定义为：

如图，𝓛 是下界函数M 的一部分（红色下划线）。

M中的第二项是KL-divergence KL散度

在当前的策略中，KL(θi, θi)=0. C*KL 项可以看作是 𝓛  的上限误差。

在当前的政策θi 中，我们可以证明 L 与 η 的第一个阶导数相同。

当 KL( θi, θi )=0 时， M 在近似于预期的奖励的局部值：这是对MM算法的要求。接下来我们讨论下界函数M的细节 。TRPO 论文附录A中的两页证明 η的有一个确定的下限 。

D_TV是总的散度方差。但这并不重要，因为我们将马上使用KL散度替代它，因为（找下界）

下界函数可以被重定义为：

注意，符号可以简记为：

  单调上升的保证

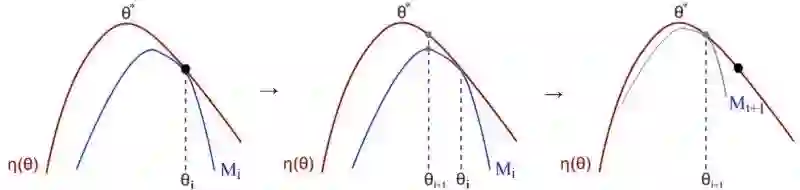
自然策略梯度的关键思想是保证了函数单调上升。它是Policy Gradient方法家族中的“用货币担保”的版本（笑）。简而言之，至少在理论上，任何策略策更新都将比之前的好。我们在这需要证明的是，基于优化M的新策略 可以保证在 η （实际预期回报）方面的表现优于之前的策略。由于策略的数量是有限的，持续更新策略最终能达到局部或全局最优。这是证明：

Mi(πi+1)对比Mi(πi)的任何改进都会使得η(πi+1)获得改进。

策略迭代中梯度单调上升的证明

这是迭代算法，它保证新策略总是比当前策略执行得更好。

然而，很难（在所有策略中）找到KL散度的最大值。因此我们将放宽要求为使用KL散度的均值。

其中 𝓛 函数：

我们可以使用重要性抽样，从策略q中抽样来估计上式左边：

因此，目标函数可以被改写为：

利用拉格朗日对偶性，可以将目标函数的约束成带拉格朗日乘子的目标函数。两者在数学上是等价的：

  直觉的看法(Intuition)

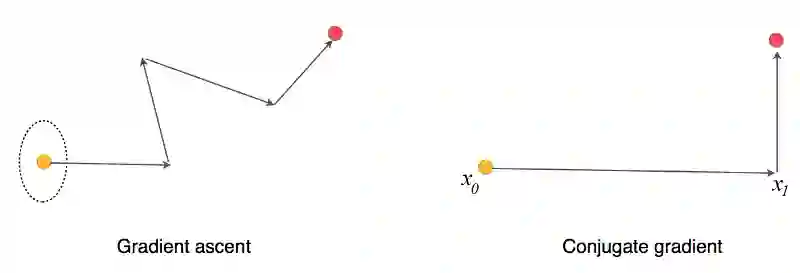
在梯度上升法中，我们判断最陡峭的方向，之后朝着那个方向前进。但是如果学习率(learning rate)太高的话，这样的行动也许让我们远离真正的回报函数( the real reward function )，甚至会变成灾难。

在信任的区域之中，我们用 δ 变量 限制我们的搜索区域。我们在前一章中用数学证明过，这样的区域可以保证在它达到局部或者全局最优策略之前，它的优化策略将会优于当前策略。

当我们继续迭代下去，我们就可以到达最优点。

  优化目标函数（Optimizing the objective function）

正如我们之前提到过的，下界函数M应该是易于优化的。事实上，我们使用泰勒级数(Taylor Series)来估计 L函数 和 KL距离(KL-divergence)的平均值，分别用泰勒将L 展开到一阶 ，KL距离 展开到二阶：

其中g是策略梯度， H 被叫做费雪信息矩阵(

那么优化问题就变成了：

我们可以通过优化二次方程来解决它，并且解集为：

TRPO 

但是，FIM (H) 及其逆运算的成本非常的高。TRPO估计如下：

通过求解x得到以下线性方程：

这证实了我们可以通过conjugate gradienH 的逆(inverse)更加简单。共轭梯度法类似于梯度下降法，但是它可以在最多N次迭代之中找到最优点，其中N表示模型之中的参数数量。

最终的算法是：

  使用裁剪目标函数的近端策略优化算法PPO 

在（使用裁剪目标函数的）PPO中，如果我们希望每次迭代可以较大的改变策略，可以使用类似梯度下降这样的一阶优化方法，并带有软约束正则像的目标来优化我们的问题。

在实现中，我们要维护两个策略网络。第一个是当前步我们想要改进的策略。

第二个是我们上步中用于采样的策略。

使用重要性抽样的思想()，我们可以从之前策略中收集的样本来估计新的策略。这样可以提高样本的使用效率。

但是随着我们对当前策略的改进，当前策略和旧策略间的差距会不断变大，估计的方差也会增加。所以，假设每4次迭代，我们就将第二个网络于当前的策略同步一次。

在PPO之中，我们要计算新旧策略的比率：

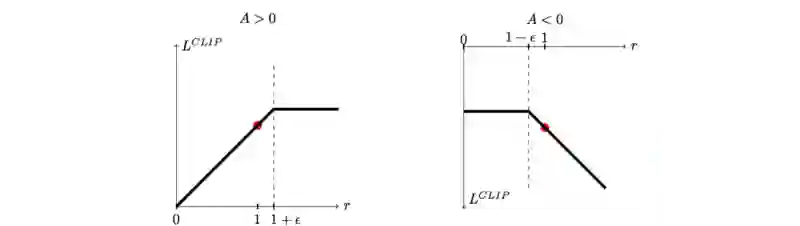
并且，如果新策略严重偏离旧策略，我们会构建一个新的目标函数来剪切(clip)被估计为优势()的函数。新的目标函数为：

如果新策略和旧策略之间的概率比落在区间 (1- ε)和 (1 + ε)外面，那么优势函数就会被剪贴。对于在PPO论文中(详见贡献和参考之中)的实验，ε设定为0.2。

实际上，剪贴这一动作会极大的减少策略的改变的数量。这里是算法：

  贡献和参考

TRPO paper

PPO paper

UC Berkeley RL course

UC Berkeley RL Bootcamp

想要继续查看该篇文章相关链接和参考文献？

长按链接点击打开或点击底部【阅读原文】：

https://ai.yanxishe.com/page/TextTranslation/1419

AI研习社每日更新精彩内容，观看更多精彩内容：

命名实体识别（NER）综述

杰出数据科学家的关键技能是什么？

初学者怎样使用Keras进行迁移学习

如果你想学数据科学，这 7 类资源千万不能错过

等你来译：

深度学习目标检测算法综述

一文教你如何用PyTorch构建 Faster RCNN

高级DQNs：利用深度强化学习玩吃豆人游戏

用于深度强化学习的结构化控制网络 （ICML 论文讲解）

春

节

挑

战

2月2日至2月12日，AI求职百题斩之每日挑战限时升级，赶紧来答题吧！

0202期  答题须知

请在公众号菜单【每日一题】→【每日一题】进入，或发送【0202】即可答题并获取解析。

点击 阅读原文 查看本文更多内容↙