RLE重铸回归方法的荣光后，回归和热图的异同究竟在何方？

会员服务 ·

RLE重铸回归方法的荣光后，回归和热图的异同究竟在何方？

2022 年 1 月 18 日 PaperWeekly

©作者 | 曾逸飞

学校 | 西安电子科技大学

研究方向 | 姿态估计与捕捉

问题来源

在 2D 姿态识别领域，基于高斯热图的方法自 2014 年提出以来，向来是独领风骚，霸占了各大榜单整整七年之久。在此期间，甚至逼得回归方法另立门派，单独建立了基于 regression 的性能榜单，可见两个方法之间的性能差异之大。

然而，对于高斯热图所拥有的优势何在，却向来是众说纷纭，缺少一个统一的答案。其中比较令人信服的理由有以下几个方面：

优势1： 全卷积的结构能够完整地保留位置信息，因此高斯热图的空间泛化能力更强。而回归方法因为最后需要将图片向量展开成一个长长的一维向量，reshape 过程中会对位置信息有所丢失。除此之外，全联接网络需要将位置信息转化为坐标值，对于这种隐晦的信息转化过程，其非线性是极强的，因此不好训练和收敛。

优势2： 关节点之间存在相互联系。以脖子和肩膀为例，这两个地方常常会挨得比较近，因此空间上是存在相关性的。高斯热图可以在一张图中保留这种相关性，因此已知脖子的位置可以帮助估计肩膀，而已知肩膀的位置也能帮助估计脖子。但是，回归坐标时是对 k 个坐标点分别回归的，没办法照顾到这种关节间的相关性。

优势3： 高斯热图有点类似分类问题中的软标注。它在目标位置上加上了一个渐进的分布过程，这能帮助网络更平滑地找到梯度下降的过程。同时软标注也减轻了在标注有误情况下的过拟合情况。（软标注的提出和作用具体可以看 Szegedy 的这篇 [1] 经典文章）

然而，最近 RLE [2] （残差似然估计）用回归的策略重回 SOTA 巅峰，做到和 HRNet 几乎持平，这就不由得令人对上述的理由进行了重新的思考。

上面三点中，哪些优势是 RLE 在回归的基础上做到的呢？
上面三点中，哪些针对热图优势解释才是真正的核心所在？或者说哪些特性造成了二者在前几年间的巨大差距？
在 RLE 补齐缺陷后，回归和热图的核心还存在差异吗？可不可以完成方法上的互相借鉴呢？

下面就让我们来一探究竟。

还没有读过 RLE 的文章可以简单读一下我这篇零基础的核心思路讲解，熟悉一下 RLE 文章的概况，不然下面牵涉到相关知识可能会读起来比较困难：

https://zhuanlan.zhihu.com/p/440567782

RLE和热图的共同优势

首先简单介绍一下 RLE 的核心思想：

数据集对关节的标注点是不能做到完美的。因此当标注值和真实的关节值存在偏差时，RLE 学习这个偏差的概率密度函数。然后设计似然函数，作为损失函数训练回归网络。为了更好的收敛，RLE 模仿残差块（Residual Block）学习残差的思想，去学习偏差密度函数较之于简单分布的残差或者，以期学习分布的过程更快更好地收敛。

如果你第一次看到 RLE，对这段话存在很多问号的话，这是也正常的。这个时候还是推荐去读读论文，或者读读上面提到的文章，以对这段话想表达的意思多做熟悉。如果你可以很清楚的明白其核心思想，那我们不妨开始思考：

RLE的这个过程，做到了高斯热图三点优势中的哪个（哪些）优势呢？

简单起见，我们就一条一条地对着看好了：

优势1 ：高斯热图空间泛化性强，而回归策略会丢失空间信息 。——RLE 仍然是用的回归，在 reshape 过程中仍然会丢失空间信息，但它依然可以做到和热图方法平分秋色。所以这条优势可能不是那么重要。

优势2： 高斯热图能在一张图中捕捉关节间的相关性，回归的过程则缺少关节间相关性的捕捉。 ——RLE 仍然没有显式地捕捉这种关节间的关系，但这不影响它是热图方法旗鼓相当的对手。所以这条优势可能也不是那么重要。

优势3： 高斯热图相当于一种软标注，它鼓励了一种渐进平滑的回归过程，也能减少对噪声数据的过拟合，而直接回归则没有这样的过程 。——RLE就恰恰是在回归完成后，通过去学习标注和预测间的 差值分布 ，从而建立起损失函数，以帮助回归的。同时，因为学习的是标注的误差情况，RLE 把你标注过程中出现的问题的规律都找出来了，也很自然能减少对那些标注不好的数据的过拟合。不难发现，RLE 和热图方法存在的一个很显著的共性就是：二者都强调了坐标的周围分布, 也都减轻了对标注的过拟合情况。

从上面的逐条比对中，我们不难发现，两个方法的重要共性就是坐标周围的分布情况。RLE 也好，热图也好，都是在这个分布上做了一些文章。热图显式地将这个分布标注出来，作为学习目标。而 RLE 则相对不那么直接地利用学习到的分布，用它建立了损失函数，来帮助网络更好的回归。

分布很重要，然后呢？

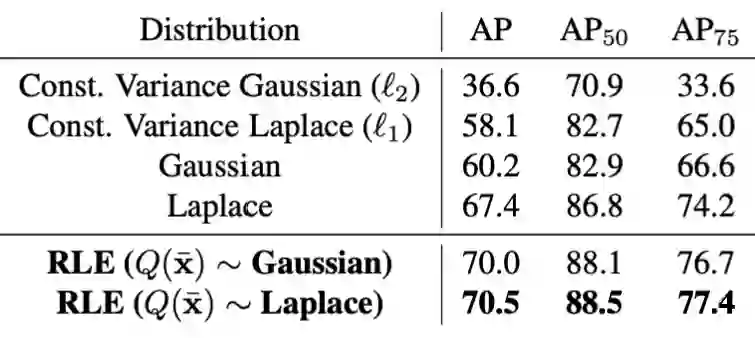
现在我们意识到，对于 2D 姿态识别而言，关节点周围的分布是一件重要的事情。RLE 在行文和实验中，也多次强调了这一点。下面是在不同分布情况下训练 resnet 得到的不同的效果，其中的差异可谓是巨大：

▲ 不同假设的分布下训练出来的结果

不同假设条件下的分布作为受控的变量，RLE 组织了一系列对比实验。从恒方差的高斯/拉普拉斯分布，到变方差的高斯/拉普拉斯分布，最后再到不同初始分布下的 RLE 学习到的分布，同一个 backbone 下性能差异可谓云泥之别。普遍而言，拉普拉斯分布更加符合关节标注的稀疏特性，因此往往可以取得更好的效果。但随着分布的灵活度和可变性的增加，二者的差距也在不断的减少。由于 RLE 采用的 flow 方法对分布具有非常出色的学习能力，因此最后两种分布的差异已经减少到只剩 0.5%mAP 了。

那么现在我们既然知道了分布的形式很重要，总得利用这个性质来做点什么吧？考虑到传统的热图是采用的分布是高斯分布，一个朴素且自然的想法就是：

将热图中的高斯分布改成拉普拉斯分布，再去训练网络。这不就让训练过程更符合数据特征了吗？

于是我就在 SimpleBaseline 的基础上改了两行：

# Copyright (c) Microsoft
# Licensed under the MIT License.
# Written by Bin Xiao (Bin.Xiao@microsoft.com)
# 文件名：JointDataset.py
# line:211左右

#原高斯分布代码：
#g = np.exp(- ((x - x0) ** 2 + (y - y0) ** 2) / (2 * self.sigma ** 2))

#改成拉普拉斯分布：
from scipy.special import kn
g=1/np.pi*kn(0,np.sqrt(2*((x-x0)**2+(y-y0)**2))/ (2 * self.sigma ** 2))
g[g>1]=1

生成的拉普拉斯热图在关节周围看上去是这样的：

▲ 拉普拉斯分布

同一样本同一关节下，和高斯热图的对比图是这样的：

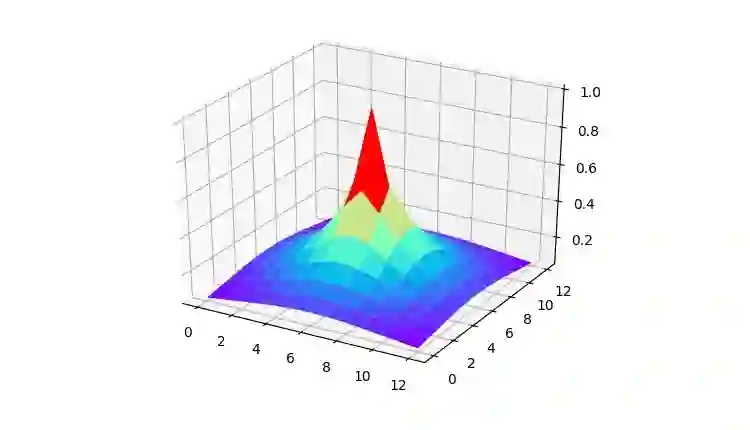
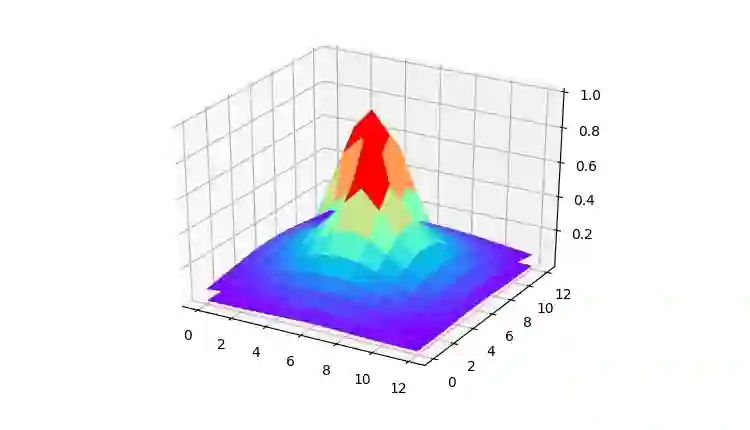
▲ 图中的分布有两层，上面较宽的是高斯，上面被包含住的是拉普拉斯，拉普拉斯从高斯一半的地方切出来了

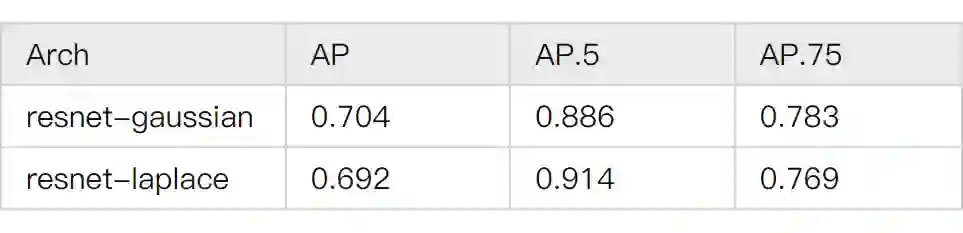
直觉上讲，用了更符合数据特征的拉普拉斯分布，效果理应更好才对。于是我在 Colab 上训练了四天两夜，含辛茹苦地呵护电脑的网络环境，终于跑完了 150 个 epoch 的 resnet50，效果却恰恰相反（模型链接在这里 [3] ）。用这种策略训练出来的模型，除了 AP.5 以外，均不如高斯分布下的热图。

即使是将损失函数换成更契合分布形式的 l1 loss 也没有让情况更加好转。更换损失函数后，训练出来的模型也只是堪堪接近 0.69mAP。这不由得让人纳闷：

为什么对回归方法而言的灵丹妙药，到了热图方法上就不见成效了呢？

这个问题的答案就牵涉到这篇文章的核心所在了：

即使二者都是在网络架构的最后模块利用了“分布”这一工具，但它们在利用过程中采取的“先验假设”不同，这也决定了它们对分布的利用方式存在“根本性”的不一致。

下面两个模块将着重阐释这一核心观点。

RLE和热图使用分布时的核心差异

要想明白高斯热图和RLE的核心差异，以及探索它们潜在的先验的不同，我们至少要从其工作流程入手吧。那好，我们先来看高斯热图的工作流程：

高斯热图：先在标注好的目标点

周围生成高斯形状的分布，我们的模型生成的热图就是要逼近这个分布。逼近的指标就由每个像素点点总均方误差

来衡量好了。

这种思路的潜台词就是：

高斯热图的先验假设：每一个人工标注的点

都是正确的，我们只要用模型尽量逼近标注点就可以了。

看完高斯热图的先验假设，我们再来看看 RLE 运作中秉持的思路是什么：

RLE: 先通过我的模型回归出坐标点和偏差量。如果坐标和标注

相差得很厉害，相差到远远大于了偏差量和我的标注误差的分布函所预测的范围，那么一方面我肯定要去优化一下我的回归模型，但另一方面在收集到新的误差

后，我还必须再去优化一下我建立的标注误差的分布函数。

这个思路的潜台词是：

RLE 的先验假设：每一个人工标注的点

都可能有偏差，所以我们要做的不仅仅是去逼近标注点，还必须去认识到这个标注偏差的分布形式。不然一旦预测有问题，对另一个潜在的问题源视而不见，而全都赖成模型的不好，模型也没办法很好的知错能改（梯度下降）。

看下来两个策略的先验假设，你觉得哪个更加有道理呢？第二个显然要中肯不少。事实上，标注的偏差在其他 cv 领域中应该也存在，但在 2D 姿态识别中，面对每一个关节都要做到像素级别的正确标注，这个难度其实是相当大的。图像分割领域可能也会有像素上标注偏差，但这种偏差一般存在在物体的边界处。除去一些小物体外，roi 的得分大头应该还是在边界的内部，所以问题可能还没那么明显。但对于姿态识别，关节标注的误差分布问题则应该成为我们考虑的对象。

那现在我们先假装确立了这样一条简化过的原则：

标注

离真实存在的点存在误差。其分布近似于拉普拉斯分布。

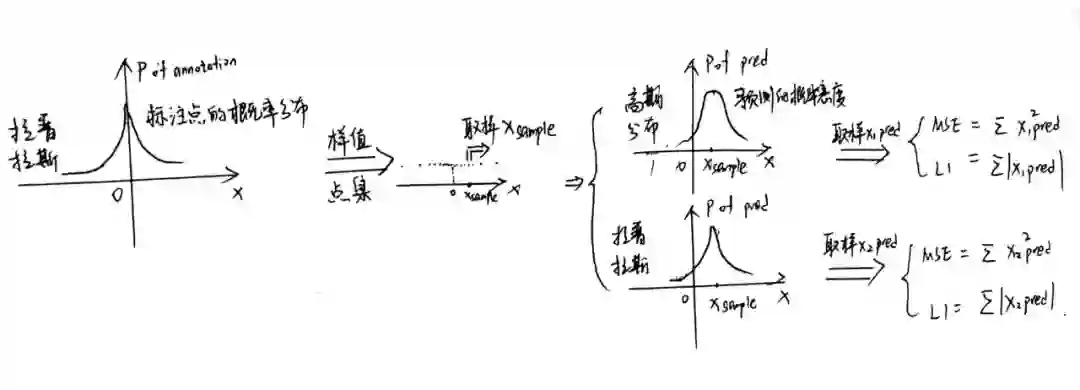
在此原则上，我们能不能通过一个简单的实验，从而给出第二部分中的拉普拉斯热图性能不升反降的解释呢？这是可以的做到的。这个实验只要用蒙特卡罗法模拟标记-预测的过程就好了。

我们先假设存在一个真正的关节点，不失一般性把它设成原点。
现在由于我们标注得不太好，标注的点在周围以拉普拉斯的形式分布。我们按照出现的概率抛硬币采样，得到采样值作为一次仿真中的标记点。
由于我们模型受到训练，可以做到以高斯/拉普拉斯的形式逼近采样点，但这种逼近不会 100% 正确，所以我们按照高斯/拉普拉斯的概率分布，以采样点为中心再抛一次硬币，从而仿真出这次模型预测的值。
最后我们重复进行大量的仿真，从而计算高斯和拉普拉斯两种分布下，预测点相对于的均方误差或者 l1 误差。

简单的图片阐释如下：

简单的代码如下：

import numpy as np
iteration=100000
mse_gau_sum=0#初始化高斯热图的总mse误差
mse_lap_sum=0#初始化拉普拉斯热图的总mse误差
l1_gau_sum=0#初始化高斯热图的总l1误差
l1_lap_sum=0#初始化拉普拉斯热图的总l1误差
for i in np.arange(iteration):
    sample=np.random.laplace(loc=0.0, scale=1.0)#第一次采样，取出(x_sample)
    pred_gau=np.random.normal(loc=sample, scale=1.0)#第二次高斯采样，取出(x_pred1)
    pred_lap=np.random.laplace(loc=sample, scale=1.0)#第二次拉普拉斯采样，取出(x_pred2)

    #loss累加
    mse_gau_sum+=pred_gau**2
    mse_lap_sum+=pred_lap**2
    l1_gau_sum+=abs(pred_gau)
    l1_lap_sum+=abs(pred_lap)
#误差的累加除以迭代总次数
mse_gau=mse_gau_sum/iteration
mse_lap=mse_lap_sum/iteration
l1_gau=l1_gau_sum/iteration
l1_lap=l1_lap_sum/iteration

结果如下表所示：

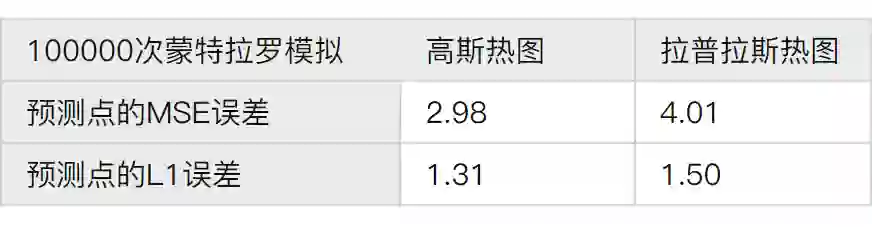
可以看出，在标注存在拉普拉斯形式的误差时，并不应该给标注点设置拉普拉斯热图。因为这种情况下，拉普拉斯热图的误差其实要大于高斯热图，因此采用高斯热图才是实际上更好的选择。这也就解释了第二部分中，采取拉普拉斯热图后效果不升反降的原因了。

定性一点来讲 ，其实这是因为拉普拉斯分布的预测比高斯分布更加自信。但在标注本身存在误差的情况下，这种自信反而对预测真实值不利。倒是温和一些的高斯分布，在对标注的错误不知情的情况下，平均预测出的结果离真实值更近。

核心差异可以解释的其他现象

其实在明白二者存在先验假设上的核心差异之前，我还曾经对 RLE 中的一个实验结果的疑问久久不能释怀。

简单来讲，这组实验是在回归的网络之外，又额外接了几个 deconv 层生成 heatmap。然后将这个 heatmap 生成的 loss 以一定比例加到 regression 的 loss 中。最后根据加权后的 loss 对网络的参数进行训练。然而，这么做不但没有让模型效果变好，反而使模型的效果下降。

这个时候很容易想到的解释是，heatmap loss 的效果很差，所以污染了 regression loss 的效果。但这个时候，实验中最难以解释的事情发生了：随着 heatmap loss 的增大，得到的 AP 先降再升，呈现出U型的曲线。如果模型性能的下降单纯是因为 heatmap 效果差，那其实可以预见的是 AP 随着 heatmap loss 的增大单调下降。但是事实和这个相反，这就很让人困惑：

一来，集成损失函数得到的效果非但没有变好，反而是变差了。二来，这又不是因为集成进来的部分本身质量差。

但当我认识到二者深层的矛盾性后，其实这两点奇怪现象的原因也就不言自明了。

“集成后的效果不降反升”，这是因为二者根本的要达成的目标本来就是南辕北辙。当 RLE 想要努力逼近 ground truth 时，heatmap loss 却拉住了 RLE,让它去逼近 annotation，这就带来了效果的下降。
“这又不是因为集成进来的部分本身质量差”，这是因为 heatmap loss 本身可以达到的效果是和 RLE 相当的，所以当它的比例提高的时候，其实模型的主体就从 RLE 过渡到了 heatmap loss，因此效果会迎来回暖。

形象一点讲的话，heatmap loss 和 RLE loss 本身就像是两根朝着不同方向拉的绳子。当只有一条绳子作用时效果最好，当加入了另一者后效果会下降，降到二者旗鼓相当时迎来效果的最低点。再往后的话，如果提高加入者的权重，效果就会回暖，也就是说这个时候绳子朝着加入者的方向偏去了，所以打破了平衡拉扯时的最低点。

总结

最后的最后，来简单总结一下这篇文章的大体内容：

首先通过目前两大 SOTA 方法的优势对比，筛选出了对于 2D 姿态估计较为重要的事物: 坐标点周围的分布。通过利用这种分布，我们既可以做到帮助网络平滑收敛，也能减少过拟合。
然后根据 RLE 中 laplace 分布的较好表现提出了朴素的猜想：是否将拉普拉斯分布应用到热图上后，模型也可以得到更好的表现呢？然而，实验却给出了否定的回答。
通过探索热图和 RLE 对于标注假设的不同，用简单的实验解释了上述现象。并得到了二者的核心差异所在：虽然都是利用坐标周围的分布训练模型，但热图假定标注是正确无疑的，RLE 则假定标注没法尽善尽美，而是和真实值之间存在偏移。
最后利用上述猜想，回答了一个令人困扰的疑问：为什么组合后的 loss 其效果呈现出独特的 U 型分布。