基于信息几何和测度学习的混合高斯模型距离研究及在图像分类中的应用

项目名称： 基于信息几何和测度学习的混合高斯模型距离研究及在图像分类中的应用

项目编号： No.61471082

项目类型： 面上项目

立项/批准年度： 2015

项目学科： 无线电电子学、电信技术

项目作者： 李培华

作者单位： 大连理工大学

项目金额： 78万元

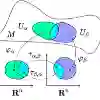
中文摘要： 混合高斯模型(GMM)广泛地应用于图像处理,模式识别和机器学习等领域.近年来基于GMM的图像分类方法取得了令人瞩目的进展.在GMM研究中一个基本而又具有挑战性的问题是如何度量GMM之间的距离.信息几何理论指出概率分布形成的空间是黎曼流形,因此只有基于黎曼测度才能准确度量流形上不同点的差异.然而由于当前方法或者未利用流形结构或者只是基于黎曼测度的近似，限制了这些方法的性能.本项目围绕GMM之间的距离这一基本问题,基于信息几何和测度学习开展理论和应用研究.首先研究一种将高斯流形嵌入到实对称正定矩阵空间再进一步映射到可再生核希尔伯特空间的方法,该方法能够保持高斯流形的黎曼几何结构.在此基础上,提出基于通用背景混合高斯模型的黎曼超向量方法度量概率分布的差异.进一步研究基于稀疏表达推土距离的大间隔机器学习方法学习GMM之间的距离测度.最后研究将黎曼超向量和大间隔GMM距离测度学习方法应用于图像分类.

中文关键词： 图像分类；信息几何；测度学习；混合高斯模型

英文摘要： Gaussian Mixture Model (GMM) has widespread applications in image processing, pattern recognition and machine learning. Recently GMM-based image classification methods have achieved great advance. One of the fundamental and challenging problems is how to measure distance between GMMs. According to the theory of information geometry, the spaces of distributions are Riemannian manifolds, and thus the most appropriate distance in the manifold should be based on Riemannian metrics. However, existing methods either fail to leverage the geometrical structure of the underlying statistical manifolds, or are just based on approximation of Riemannian metrics, which restrict their performance. To address the shortcomings of the existing methods, we perform research in both theory and application focusing on the fundamental problem of the distance between GMMs. Firstly, we study a novel method embedding the Gaussian manifold into the space of symmetric positive definite (SPD) matrices and further map the latter into the reproducing kernel Hilbert space (RKHS); this method preserves the Riemannian geometrical structure of Gaussian manifold. Secondly, we propose the Riemannian super-vector based on the universal background Gaussian mixture model (UBM-GMM) to measure the difference of probability distributions. Furthermore, we present the large margin machine learning method to learn the distance metrics between GMMs. Finally, we study the applications of Riemannian super-vector and large margin GMM distance metric learning method in image classification.

英文关键词： Image classification;Information geometry;metric learning;Gaussian mixture model