【PHM算法】PHM算法 | 故障诊断建模方法

会员服务 ·

【PHM算法】PHM算法 | 故障诊断建模方法

2020 年 3 月 16 日 产业智能官

天泽智云CyberInsight

本文将从故障诊断的概念、常用算法及应用案例三个方面，解读故障诊断建模方法。

什么是故障诊断？

诊断是指通过检查观察到的症状来确定问题的本质。故障诊断的目标是将高维特征向量转换为状态标识，即标识出健康/故障，其中故障又分为多种失效模式。

数据驱动的故障诊断分为两个阶段：训练阶段和测试阶段。

训练阶段：训练故障诊断模型

在训练阶段，需要大量的历史数据、样本及多维特征。有些历史数据可以通过机理/经验丰富专家的经验对当前状态打标签（如是否健康/故障是什么等级等），但工业领域的数据多数情况都缺少标签，要么全部都是健康数据，要么根本不知道是故障/健康数据。这两种情况分别对应有监督学习和无监督学习，可以运用相应算法训练出故障诊断模型。

测试阶段：测试当前状态识别

在测试阶段，将设备的特征提取出来，放到训练好的故障诊断模型里，从而计算出当前的状态标识。

故障诊断常用算法

支持向量机（SVM）

支持向量机（SVM）最早于1963年由VladimirN. Vapnik和Alexey Ya. Chervonenkis提出，在解决小样本、非线性及高维模式识别中表现出许多特有优势，并能够推广应用到函数拟合等其他机器学习问题中。

>> 线性问题

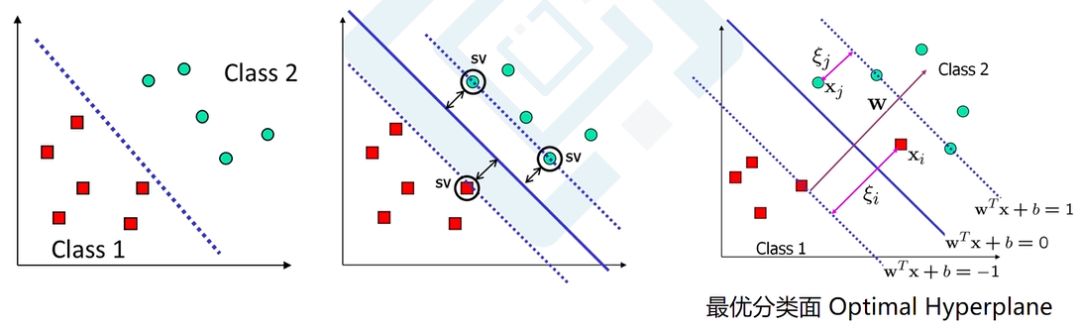
支持向量机（SVM）可以实现线性问题分类，有效解决二分类问题。

核心思想：找到最优分类面将正负样本分开，使得样本到分类面的距离尽可能远。

如上图所示，在二维图中是一条直线，在多维高维空间里则是一个超平面。通过运用数学规划和优化算法，让正负样本到超平面的距离尽可能的远，从而找到最优分类面。

>> 非线性可分问题

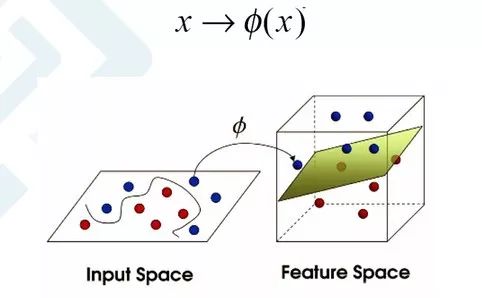
支持向量机算法除了能对线性问题进行分类之外,还可以对非线性可分的问题进行分类,我们可以使用1992年提出的核函数技巧（The Kernel Trick）的方法，利用函数把低维特征映射到高维的空间。

如图所示，左边图样本特征在二维空间里是不可线性可分的，但是把它映射到高维空间中，就以找到一个平面将其分开。

常用的核函数包括多项式函数（Polynomial）、高斯函数（Gaussian）、径向基函数（Radial Basis Function）、Sigmoid函数等。在Python和Matlab中都有非常成熟的算法包供大家调用，而且也可以选择不同的核函数来解决线性不可分的问题。

>> 多分类的故障诊断问题

SVM虽然是二分类问题，但是也可以解决多分类的故障诊断问题，具体如何实现？

举例而言，比如说已知共有ABCD四类，A是健康，BCD是三种不同故障模式，首先可以用一个分类器去分类是健康/故障，即是A/不是A；之后在不是A的部分中再训练一个分类器来分类，是B故障/不是B故障。简言之就是用层层迭代的方法，通过多种SVM分类器的组合来实现多分类问题。

除了SVM支持向量机的方法，机器学习中还有许多其他常用的分类算法，如随机森林、AdaBoosting、人工神经网络等，这些都是能非常强大的工具，可以更清晰地解决分类问题。

以上几种方法都需要有明确的故障标签，是一个有监督的学习过程。而在工业场景中的数据大多是无标签的/健康的，无法满足以上方法的基础条件，这就需要通过其他方法来进行解决。

自组织映射神经网络（SOM）

SOM的优点在于能够不断学习训练数据的内在模态和模式，形成神经网络模型，把高维特征矩阵转化为二维蜂窝状的映射图，实现整个故障的分类。

其核心机制是竞争学习。首先根据训练数据的样本大小和特征的维度，来构造初始SOM网络的模型结构，上面的每一个神经元通过不同的群众向量来表达；之后基于竞争学习的更新策略不断迭代更新，移动神经元的位置形成不同的BMU，最大程度靠近所属聚类。

SOM在进行故障诊断和健康评估时并非完全相同，区别如下：

在进行故障诊断时，把状态样本放到训练好的SOM模型中计算出BMU，找到所属类别，则认为是当前状态的故障类别。
而在健康评估的时候，需要在此基础上进一步计算当前状态和BMU之间的距离，作为健康状态的评价指标。

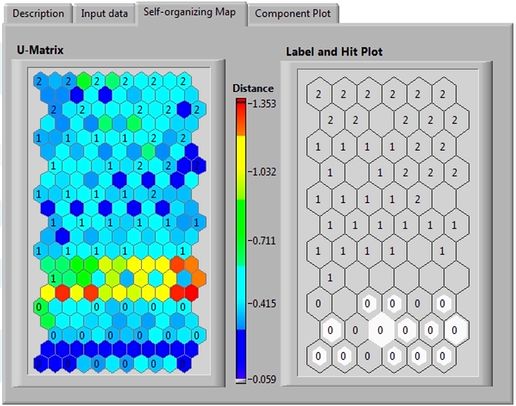
SOM的数据可视化的效果非常好，可以把高维的数据转化为一个蜂窝状的映射图。

映射图是如上所示的U-matrix，其中的不同颜色表示相邻神经元之间的距离，越偏蓝色距离越近，越偏红色距离越远，当出现一片红色的时候就表示是一个分类面。

在实际应用中，通常采用Hit map，将测试数据放到训练好的U-matrix中，找到Hit Point所在位置，从而确定故障诊断的分类。

>> SOM的优缺点

优点：

SOM的主要优点是能够进行无监督学习，即训练样本中不需要知道有多少分类，也无需故障和健康的标签，就可以将其分类出来
纯粹的数据驱动，可以将数据分类到不同的集群中，不需要数据的先验知识
SOM在许多不同的场景中得到了广泛的应用，并具有广泛的用途

缺点：

为了生成一个没有缺失值的映射图，需要为每个样本的每个维度设置一个值
每个SOM模型都是不同的，从同样的样本向量中可能会发现不同的相似性，有一些随机性的干扰
为了得到一个好的映射图，需要构建许多映射图
需要非常大的计算量

贝叶斯网络（BBN）

上面的几种算法都是从数据本身出发，无需任何的数据的先验知识。而工业领域老专家们的经验是非常重要的一部分，有些老师傅通过听声音/看某些指标的方式就可以判断出设备的故障类型。

在贝叶斯网络中，可以把老专家们的经验统计起来，形成条件概率（A=j | B=i）来描述不同时间之间的因果关系。

贝叶斯定理：P(A|B)=P(A,B)/P(B)

贝叶斯网络是用图模型（Graphical Model）的结构，把整个复杂系统中所有可能发生的情况结构化地表达出来。

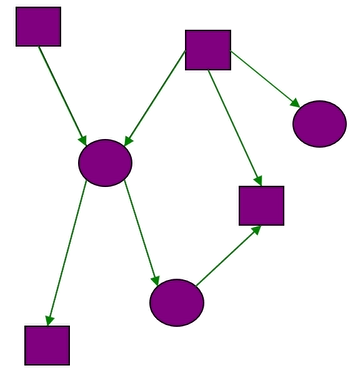
>> 有向无环图

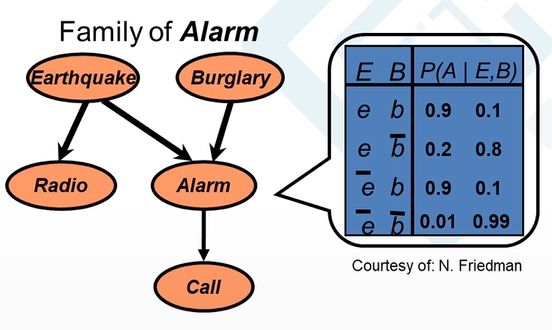
如上图所示，节点表示随机变量，箭头表示条件依赖，有向边给出因果关系。通过统计所有的依赖关系，得出条件概率分布图。

通过一个例子来具体说明，在某家庭报警系统中，地震和入室盗窃都可能引发报警，地震报警的同时会有广播提醒。当地震和入室盗窃同时发生时，90%的概率会报警，而同时不发生的时候，99%的概率不报警，这就是基于经验或机理所得。当系统更为复杂时，上表也随之更为庞大。

>> 如何用贝叶斯网络进行故障诊断？

定义模型的结构、节点数、形式和状态
定义每个节点的条件概率分布（上面例子表中的数据）
利用测试数据，使用多种算法训练BBN
分析输出并确定网络中最敏感的因素
使用不同的算法进行对比

案例分析：轴承故障诊断

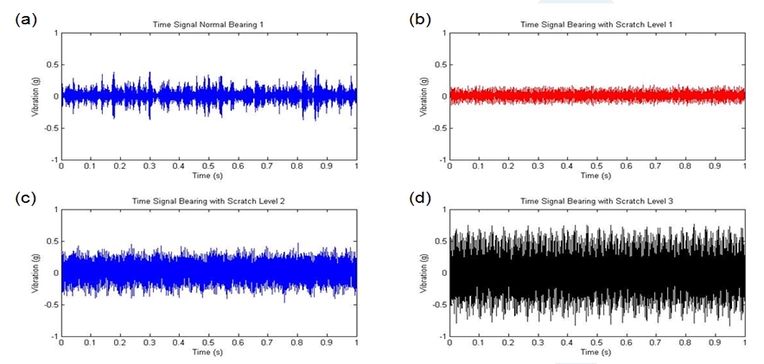
轴承作为典型的旋转类设备，一般通过振动信号进行故障诊断。如下图所示，图a是采集到的多种模式的振动信号，可能由有多种故障耦合在一起，无法直观地判断其故障。下面通过自组织映射神经网络（SOM）的方法进行故障诊断。

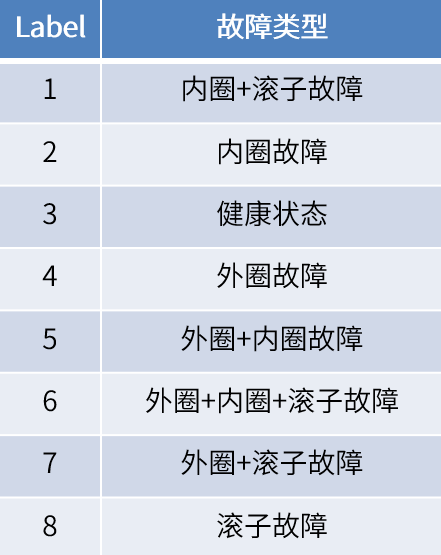
准备数据集，确定类标签（如下图所示，共八种故障类型）
根据需要的详细程度确定显示大小
选择SOM模型的网格形式
设置SOM超参数，包括初始权重、学习率等
训练数据生成SOM模型
训练SOM模型，并用Hit-point测试SOM模型

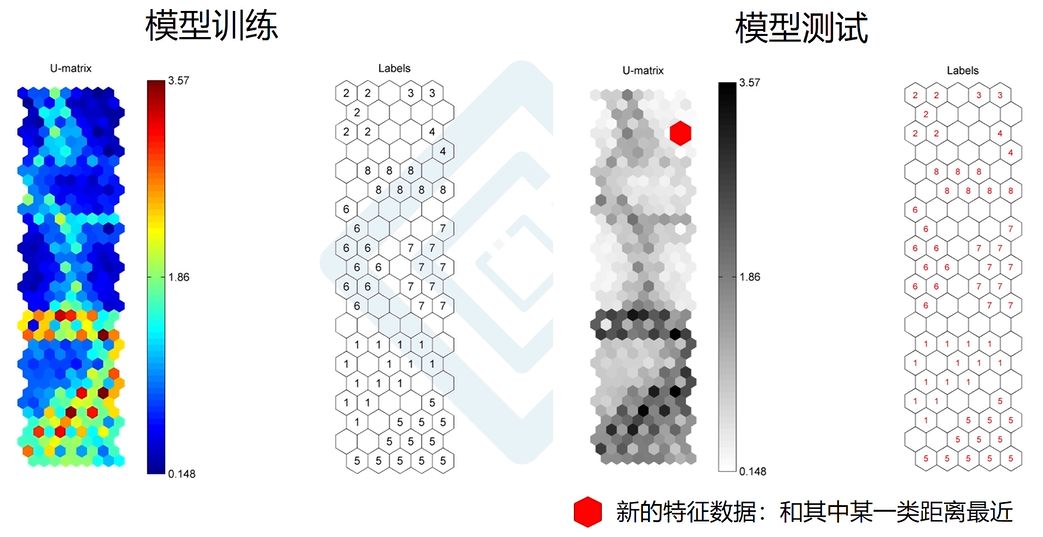
其中，训练出的模型如下图左所示，可以通过SOM将八类故障清晰地区分出来（亮色代表分界线）。

在模型测试时，将新的特征数据（即需要测试的样本）放到SOM U-matrix模型计算后，其位置如上图右红点所示，与八种故障类型的标签进行对比可判断出其属于第四类——外圈故障。

总结

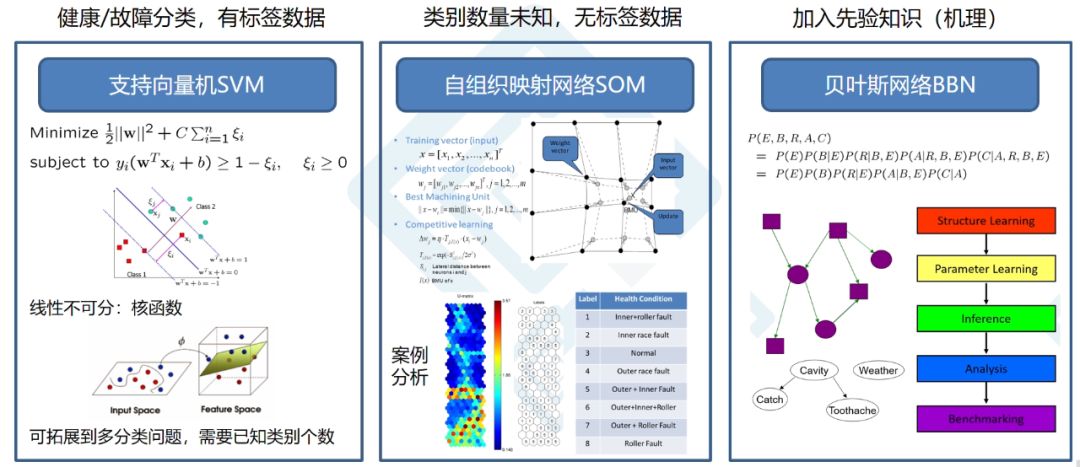
故障诊断问题就是将高维的特征向量转换为状态标识（健康状态、故障模式1、故障模式2、故障模式3……）。

对于有标签的数据，通常采用分类算法，其中最常见的是支持向量机（SVM），但是在SVM中如果遇到一些线性不可分的情况，可以用核函数的技巧把低维特征映射到高维空间中，此外也可以拓展到多分类问题。

面对类别数量未知、无标签的数据，通常采用自组织映射神经网络（SOM），可视化效果好。

以上两者均是单纯从数据驱动的角度得到模型，如果要加入先验知识（机理），则采用贝叶斯网络，可以将每种特征和故障类型之间的关联关系，通过机理给固化下来。

先进制造业+工业互联网

产业智能官 AI-CPS

加入知识星球“产业智能研究院”：先进制造业OT（自动化+机器人+工艺+精益）和工业互联网IT（云计算+大数据+物联网+区块链+人工智能）产业智能化技术深度融合，在场景中构建“状态感知-实时分析-自主决策-精准执行-学习提升”的产业智能化平台；实现产业转型升级、DT驱动业务、价值创新创造的产业互联生态链。

产业智能化平台作为第四次工业革命的核心驱动力，将进一步释放历次科技革命和产业变革积蓄的巨大能量，并创造新的强大引擎；重构设计、生产、物流、服务等经济活动各环节，形成从宏观到微观各领域的智能化新需求，催生 新技术、新产品、新产业、新业态和新模式； 引发经济结构重大变革，深刻改变人类生产生活方式和思维模式，实现社会生产力的整体跃升。

产业智能化技术分支用来的今天，制造业者必须了解如何将“智能技术”全面渗入整个公司、产品、业务等商业场景中， 利用工业互联网形成数字化、网络化和智能化力量，实现行业的重新布局、企业的重新构建和焕然新生。