从零开始学习:梯度下降和随机梯度下降!
在之前的教程里,我们通过损失函数
在本节教程中,我们将详细介绍梯度下降算法和随机梯度下降算法。由于梯度下降是优化算法的核心部分,深刻理解梯度的意义十分重要。为了帮助大家深刻理解梯度,我们将从数学上阐释梯度下降的意义。
一维梯度下降
我们先以简单的一维梯度下降为例,解释梯度下降算法可以降低目标函数值的原因。一维梯度是一个标量,也称导数。
假设函数 的输入和输出都是标量。根据泰勒展开公式,我们得到
假设是一个常数,将
替换为
后,我们有
如果
是一个很小的正数,那么
也就是说,如果当前导数 ,按照 更新可能降低的值。
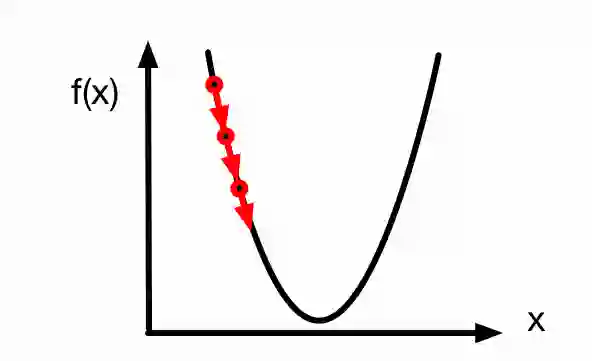
由于导数 是梯度在一维空间的特殊情况,上述更新 的方法也即一维空间的梯度下降。一维空间的梯度下降如下图所示,参数 沿着梯度方向不断更新。
学习率
上述梯度下降算法中的 (取正数)叫做学习率或步长。需要注意的是,学习率过大可能会造成 迈过(overshoot)最优解,甚至不断发散而无法收敛,如下图所示。
然而,如果学习率过小,优化算法收敛速度会过慢。实际中,一个合适的学习率通常是需要通过实验调出来的。
多维梯度下降
现在我们考虑一个更广义的情况:目标函数的输入为向量,输出为标量。
假设目标函数 的输入是一个多维向量。目标函数有关 的梯度是一个由偏导数组成的向量:
为表示简洁,我们有时用 代替 。梯度中每个偏导数元素 ∂f(x)/∂xi代表着 在 有关输入 xi的变化率。为了测量 沿着单位向量 方向上的变化率,在多元微积分中,我们定义 在 上沿着 方向的方向导数为
由链式法则,该方向导数可以改写为
方向导数给出了 上沿着所有可能方向的变化率。为了最小化,我们希望找到 能被降低最快的方向。因此,我们可以通过 来最小化方向导数。
由于, 其中为和 之间的夹角,当,取得最小值-1。因此,当 在梯度方向的相反方向时,方向导数被最小化。所以,我们可能通过下面的梯度下降算法来不断降低目标函数 的值:
相同地,其中(取正数)称作学习率或步长。
随机梯度下降
然而,当训练数据集很大时,梯度下降算法可能会难以使用。为了解释这个问题,考虑目标函数
其中 是有关索引为的训练数据点的损失函数。需要强调的是,梯度下降每次迭代的计算开销随着 线性增长。因此,当 很大时,每次迭代的计算开销很高。
这时我们需要随机梯度下降算法。在每次迭代时,该算法随机均匀采样并计算
。事实上,随机梯度是对梯度的无偏估计
小批量随机梯度下降
广义上,每次迭代可以随机均匀采样一个由训练数据点索引所组成的小批量
来更新
:
其中 代表批量中索引数量, (取正数)称作学习率或步长。同样,小批量随机梯度也是对梯度的无偏估计:
这个算法叫做小批量随机梯度下降。该算法每次迭代的计算开销为。因此,当批量较小时,每次迭代的计算开销也较小。
算法实现和实验
我们只需要实现小批量随机梯度下降。当批量大小等于训练集大小时,该算法即为梯度下降;批量大小为1即为随机梯度下降。
In [1]:
# 小批量随机梯度下降。def sgd(params, lr, batch_size): for param in params: param[:] = param - lr * param.grad / batch_size
实验中,我们以线性回归为例。其中真实参数w为[2, -3.4],b为4.2。
In [2]:
import mxnet as mx
from mxnet import autograd
from mxnet import ndarray as nd
from mxnet import gluonimport
randommx.random.seed(1)
random.seed(1)
# 生成数据集。
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
X = nd.random_normal(scale=1, shape=(num_examples, num_inputs))
y = true_w[0] * X[:, 0] + true_w[1] * X[:, 1] + true_b
y += .01 * nd.random_normal(scale=1, shape=y.shape)
dataset = gluon.data.ArrayDataset(X, y)
# 构造迭代器。
import random
def data_iter(batch_size): idx = list(range(num_examples)) random.shuffle(idx) for batch_i, i in enumerate(range(0, num_examples, batch_size)): j = nd.array(idx[i: min(i + batch_size, num_examples)]) yield batch_i, X.take(j), y.take(j)
# 初始化模型参数。
def init_params(): w = nd.random_normal(scale=1, shape=(num_inputs, 1)) b = nd.zeros(shape=(1,)) params = [w, b] for param in params: param.attach_grad() return params
# 线性回归模型。
def net(X, w, b): return nd.dot(X, w) + b
# 损失函数。
def square_loss(yhat, y): return (yhat - y.reshape(yhat.shape)) ** 2 / 2
接下来定义训练函数。当epoch大于2时(epoch从1开始计数),学习率以自乘0.1的方式自我衰减。训练函数的period参数说明,每次采样过该数目的数据点后,记录当前目标函数值用于作图。例如,当period和batch_size都为10时,每次迭代后均会记录目标函数值。
In [3]:
%matplotlib inline
import matplotlib as mplmpl.rcParams['figure.dpi']= 120
import matplotlib.pyplot as plt
import numpy as np
def train(batch_size, lr, epochs, period): assert period >= batch_size and period % batch_size == 0 w, b = init_params() total_loss = [np.mean(square_loss(net(X, w, b), y).asnumpy())] # 注意epoch从1开始计数。 for epoch in range(1, epochs + 1): # 学习率自我衰减。 if epoch > 2: lr *= 0.1 for batch_i, data, label in data_iter(batch_size): with autograd.record(): output = net(data, w, b) loss = square_loss(output, label) loss.backward() sgd([w, b], lr, batch_size) if batch_i * batch_size % period == 0: total_loss.append( np.mean(square_loss(net(X, w, b), y).asnumpy())) print("Batch size %d, Learning rate %f, Epoch %d, loss %.4e" % (batch_size, lr, epoch, total_loss[-1])) print('w:', np.reshape(w.asnumpy(), (1, -1)), 'b:', b.asnumpy()[0], '\n') x_axis = np.linspace(0, epochs, len(total_loss), endpoint=True) plt.semilogy(x_axis, total_loss) plt.xlabel('epoch') plt.ylabel('loss') plt.show()
当批量大小为1时,训练使用的是随机梯度下降。在当前学习率下,目标函数值在早期快速下降后略有波动。当epoch大于2,学习率自我衰减后,目标函数值下降后较平稳。最终学到的参数值与真实值较接近。
In [4]:
train(batch_size=1, lr=0.2, epochs=3, period=10)
Batch size 1, Learning rate 0.200000, Epoch 1, loss 5.0910e-05 Batch size 1, Learning rate 0.200000, Epoch 2, loss 6.4832e-05 Batch size 1, Learning rate 0.020000, Epoch 3, loss 4.9259e-05 w: [[ 2.00118256 -3.4002037 ]] b: 4.19923
当批量大小为1000时,由于训练数据集含1000个样本,此时训练使用的是梯度下降。在当前学习率下,目标函数值在前两个epoch下降较快。当epoch大于2,学习率自我衰减后,目标函数值下降较慢。最终学到的参数值与真实值较接近。
In [5]:
train(batch_size=1000, lr=0.999, epochs=3, period=1000)
Batch size 1000, Learning rate 0.999000, Epoch 1, loss 7.3842e-02 Batch size 1000, Learning rate 0.999000, Epoch 2, loss 9.8761e-04 Batch size 1000, Learning rate 0.099900, Epoch 3, loss 8.2789e-04 w: [[ 2.01470947 -3.37011194]] b: 4.17426
当批量大小为10时,由于训练数据集含1000个样本,此时训练使用的是小批量随机梯度下降。最终学到的参数值与真实值较接近。
In [6]:
train(batch_size=10, lr=0.2, epochs=3, period=10)
Batch size 10, Learning rate 0.200000, Epoch 1, loss 4.9434e-05 Batch size 10, Learning rate 0.200000, Epoch 2, loss 5.1733e-05 Batch size 10, Learning rate 0.020000, Epoch 3, loss 4.8792e-05 w: [[ 2.00055027 -3.40005398]] b: 4.20035
同样是批量大小为10,我们把学习率改大。这时我们观察到目标函数值不断增大。这时典型的overshooting问题。
In [7]:
train(batch_size=10, lr=5, epochs=3, period=10)
Batch size 10, Learning rate 5.000000, Epoch 1, loss nan Batch size 10, Learning rate 5.000000, Epoch 2, loss nan Batch size 10, Learning rate 0.500000, Epoch 3, loss nan w: [[ nan nan]] b: nan
同样是批量大小为10,我们把学习率改小。这时我们观察到目标函数值下降较慢,直到3个epoch也没能得到接近真实值的解。
In [8]:
train(batch_size=10, lr=0.002, epochs=3, period=10)
Batch size 10, Learning rate 0.002000, Epoch 1, loss 1.3283e+01 Batch size 10, Learning rate 0.002000, Epoch 2, loss 8.8150e+00 Batch size 10, Learning rate 0.000200, Epoch 3, loss 8.4618e+00 w: [[ 0.30856001 -0.91306931]] b: 1.43488
结论
当训练数据较大,梯度下降每次迭代计算开销较大,因而(小批量)随机梯度下降更受青睐。
学习率过大过小都有问题。合适的学习率要靠实验来调。
练习
为什么实验中随机梯度下降的学习率是自我衰减的?
梯度下降和随机梯度下降虽然看上去有效,但可能会有哪些问题?
原文:http://zh.gluon.ai/chapter_optimization/gd-sgd-scratch.html
招聘|AI学院长期招聘AI课程讲师(兼职):日薪5k-10k