精品公开课 | 随机梯度下降算法综述

授课老师：七月在线 -- 管老师

论文原作：Sebastian Ruder

论文翻译：七月在线翻译组

视频直达：文末 阅读原文

文章结构

1. 简介：梯度下降法 

2. 随机梯度下降

3. 随机梯度下降的问题与挑战

4. 随机梯度下降的优化算法（本文主要内容）

5. 并行与分布式架构

6. 随机梯度下降的其他优化方法

随机梯度下降法主要为了解决第一个问题：梯度计算
由于随机梯度下降法的引入，我们通常将梯度下降法分为三种类型：
1. 批梯度下降法(GD)
原始的梯度下降法
2. 随机梯度下降法(SGD)
每次梯度计算只使用一个样本
• 避免在类似样本上计算梯度造成的冗余计算
• 增加了跳出当前的局部最小值的潜力
• 在逐渐缩小学习率的情况下，有与批梯度下降法类似的收敛速度
3. 小批量随机梯度下降法(Mini Batch SGD)
每次梯度计算使用一个小批量样本
• 梯度计算比单样本更加稳定
• 可以很好的利用现成的高度优化的矩阵运算工具

随机梯度下降法的主要困难在于前述的第二个问题：学习率的选取

1. 局部梯度的反方向不一定是函数整体下降的方向
• 对图像比较崎岖的函数，尤其是隧道型曲面，梯度下降表现不佳
2. 预定学习率衰减法的问题
• 学习率衰减法很难根据当前数据进行自适应
3. 对不同参数采取不同的学习率的问题
• 在数据有一定稀疏性时，希望对不同特征采取不同的学习率
4. 神经网络训练中梯度下降法容易被困在鞍点附近的问题
• 比起局部极小值，鞍点更加可怕

动量法（Momentum）（适用于隧道型曲面）
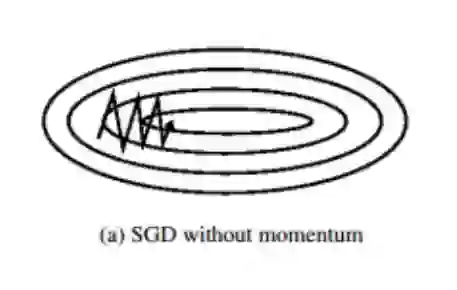
梯度下降法在狭长的隧道型函数上表现不佳，如下图所示
• 函数主体缓缓向右方下降
• 在主体方向两侧各有一面高墙，导致垂直于主体方向有更大的梯
度
• 梯度下降法会在隧道两侧频繁震荡。

为什么不用牛顿法？
• 牛顿法要求计算目标函数的二阶导数(Hessian matrix)，在高维特
征情形下这个矩阵非常巨大，计算和存储都成问题
• 在使用小批量情形下，牛顿法对于二阶导数的估计噪音太大
• 在目标函数非凸时，牛顿法更容易收到鞍点甚至最大值点的吸引

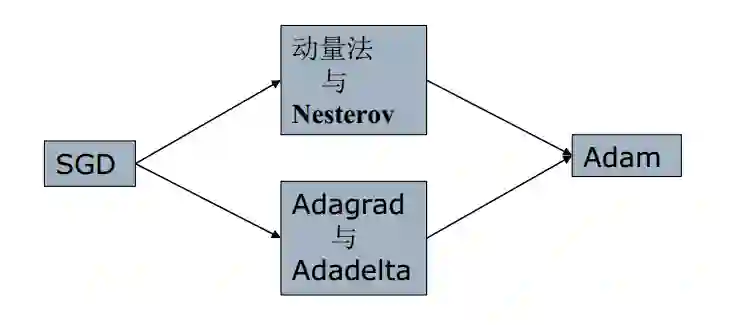
究竟如何选择算法呢？
• 动量法与Nesterov的改进方法着重解决目标函数图像崎岖的问题
• Adagrad与Adadelta主要解决学习率更新的问题
• Adam集中了前述两种做法的主要优点

一些SGD的并行与分布式架构
• Hogwild
• Downpour SGD
• Delay-tolerance Algorithms
• TensorFlow
• Elastic Averaging SGD

一些与前述方法不同的作法来进一步优化 SGD
• Shuffling and Curriculum Learning
• 每次大循环前洗牌（Shuffling）
• 人为对数据排序（Curriculum Learning）
• 批规范化 与 批再规范化
• 每次小批量计算前进行规范化
• Early Stopping
• 在误差减小程度小于阈值时终止训练
• Gradient Noise
• 在每一次更新中加入人为噪音，帮助逃离鞍点和局部极小值点。

（完）

---

点击 阅读原文 获取论文全文pdf 和老师讲解视频