CUDA 并行计算优化策略总结

会员服务 ·

CUDA 并行计算优化策略总结

2021 年 12 月 27 日 极市平台

↑ 点击蓝字关注极市平台

作者 | LustofLife@知乎

来源 | https://zhuanlan.zhihu.com/p/297201517

编辑 | 极市平台

极市导读

并行计算为了提高算法运行效率，本文通过以矩阵乘法（C = A * B）的各种实现思路以及优化方法总结为例子，过一遍cuda的几个基础优化策略。 >>加入极市CV技术交流群，走在计算机视觉的最前沿

本文脉络

关于矩阵乘法的问题描述关于矩阵乘法的问题描述
优化策略的核心思想
例子

CPU上的代码实现：https://github.com/hova88/cuda-template/blob/main/src/matmul/naive.cu
GPU上的代码实现：https://github.com/hova88/cuda-template/blob/main/src/matmul/naive.cu
优化策略一：https://github.com/hova88/cuda-template/blob/main/src/matmul/tiling.cu
优化策略二：https://github.com/hova88/cuda-template/blob/main/src/matmul/coalescing.cu
优化策略三：No Bank Conflict
优化策略四：https://github.com/hova88/cuda-template/blob/main/src/matmul/comopt.cu
优化策略五：https://github.com/hova88/cuda-template/blob/main/src/matmul/unroll.cu
优化策略六：Prefetching

1 关于矩阵乘法的问题描述

参照NVIDIA官网教程——https://developer.nvidia.com/blog/cutlass-linear-algebra-cuda/

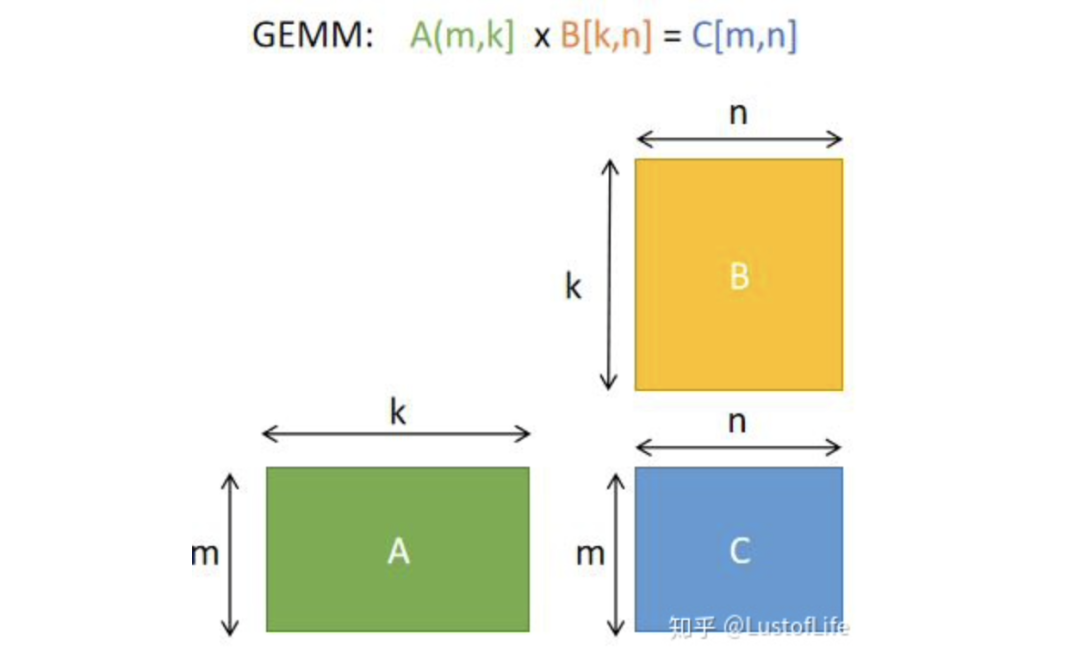
首先解决矩阵乘法问题更具体来说是解决GEMM(GEneral Matrix to Matrix Multiplication,通用矩阵乘法)问题。即C=αA*B+βC。其中A、B和C是矩阵。A是M×K矩阵，B是K×N矩阵，C是M×N矩阵。为了方便说明，后续的例子中假设标量alpha=beta=1。

那么如何更高效的进行GEMM呢?

2：优化策略的核心思想

1.减小缓存（cached）
2.使写入速度跟上指令的计算速度

对于GEMM计算，最直接的想法就是loop，elements相乘再相加

for (int i = 0; i < M; ++i)                   //---->遍历A的行，行id记做i
    for (int j = 0; j < N; ++j)               //---->遍历B的列，列id记做j
       for (int k = 0; k < K; ++k)            //---->在行列i,j确定的前提下，进行对应元素的 相乘 和 加和 ,元素id记做k 
            C[i][j] += A[i][k] * B[k][j];     //---->最后输出到C的第i,j个元素

对于M=N=K的大型方阵，矩阵乘积中的数学运算数为O(N^3)，而所需的数据量为O(N^2)，从而产生N阶的计算强度。然而，利用理论计算强度(heoretical compute intensity)需要将重复使用每个元素O(N)。但是，上面的内积算法依赖于缓存(fast on-chip caches)中保存一个大的工作集，这会导致随着M、N和K增长时，CPU需要来回搬运数据，会累的要死。（不符合减小缓存的思想）

PS：一般来说，求两矩阵内积，K的维度数要远大于N,M(例如SVM中的核函数技巧)，所以将大计算量的K维放在内循环不是一个聪明的决定。

一个更好的公式是通过构造K维上的循环作为最外层的循环来置换循环嵌套。这种形式的计算一次加载a列和B行，计算其外积，并将此外积的结果累加到矩阵C中。此后，a列和B行的结果将不再使用。

for (int k = 0; k < K; ++k)     // K dimension now outer-most loop
    for (int i = 0; i < M; ++i)
        for (int j = 0; j < N; ++j)
            C[i][j] += A[i][k] * B[k][j];

更进一步思考,如何进一步减少寄存空间的缓存大小？

上述方法的一个问题是，它要求矩阵C的所有M-by-N元素都是激活的，以存储每个乘法累加指令的结果。这样很难保证内存中的写入速度能够跟上CPU中的计算速度。

而如何去使得内存的写入速度与计算乘法累加指令的速度一样快呢？

-- 采用分块（Tile）的策略

重点来了，

首先，我们可以通过将矩阵C的工作空间Partitioning为大小为（M*tile-by-N*tile）的Tile来矩阵C的工作空间大小(the working set size of C)，这些Tile的大小需要与存储器(on-chip memory)相适应。

然后，我们将用外积代替内积的策略应用到每一块Tile上。就像以下循环嵌套这样。

for (int m = 0; m < M; m += Mtile)                // iterate over M dimension
    for (int n = 0; n < N; n += Ntile)            // iterate over N dimension
        for (int k = 0; k < K; ++k)       //----> like above example
            for (int i = 0; i < Mtile; ++i)       // compute one tile 
                for (int j = 0; j < Ntile; ++j) {
                    int row = m + i;
                    int col = n + j;
                    C[row][col] += A[row][k] * B[k][col];
                }

对于C上的每一块Tile,都只取了一次A和B中的Tiles，使其达到*O(N)*的计算强度。示意图就类似下面这样。（如果对 global memory / shared memory / register file/ SM cores 不太清楚的话，还是建议好好研究研究一下，对后续的优化策略理解很有帮助！）

对于GPU来说，The size of each tile of C may be chosen to match the capacity of the L1 cache or registers of the target processor, and the outer loops of the nest may be trivially parallelized. This is a great improvement !

Here, you can see data movement from global memory to shared memory (matrix to thread block tile), from shared memory to the register file (thread block tile to warp tile), and from the register file to the CUDA cores for computation (warp tile to thread tile).

参考链接

Matrix Multiplication CUDA——https://ecatue.gitlab.io/gpu2018/pages/Cookbook/matrix_multiplication_cuda.html

如果觉得有用，就请分享到朋友圈吧！

△点击卡片关注极市平台，获取最新CV干货

公众号后台回复“transformer”获取最新Transformer综述论文下载～