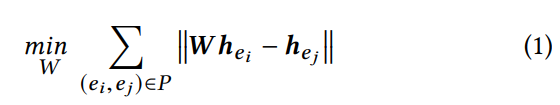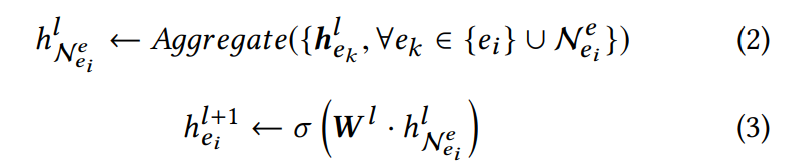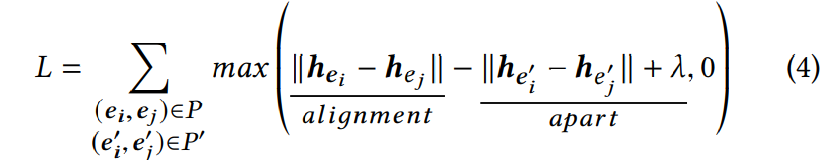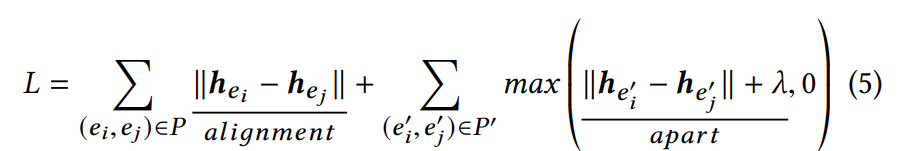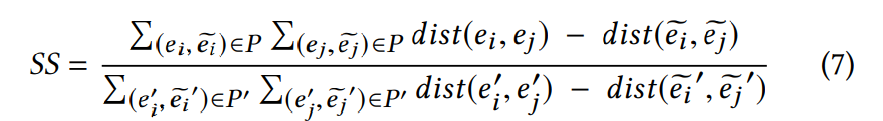论文浅尝 - CIKM2020 | Relation Reflection Entity Alignment

论文笔记整理：谭亦鸣，东南大学博士生。

---

来源：CIKM 2020

链接：https://arxiv.org/pdf/2008.07962.pdf

研究背景与任务描述:

实体对齐旨在基于已有对齐实体标注的情况下，确定不同KG中未知的对等实体，其本质是multi-source KGs的一体化.

随着GNN在对齐工作的引入，现有模型的方法愈加复杂。作者在相关的研究中发现了两个不寻常的情况：Q1. GNN中的标准线性转换效果并不好；Q2. 许多面向预测任务的新KG embedding方法在对齐任务上的效果较差。本文将现有的实体对齐方法抽象为统一的框架：Shape-Builder & Alignment，该框架不仅解释了上述情况的原因，并且给出了对于理想转换操作的两个关键标准。作者基于此构建了一个新的GNN-based method “Relation Reflection Entity Alignment, RREA”，该方法的主要思路是利用relation reflection transformation更有效率的获取到每个实体的relation specific embedding。真实数据上的实验表明该方法是SOAT

目前的Entity Alignment方法主要分为两类：

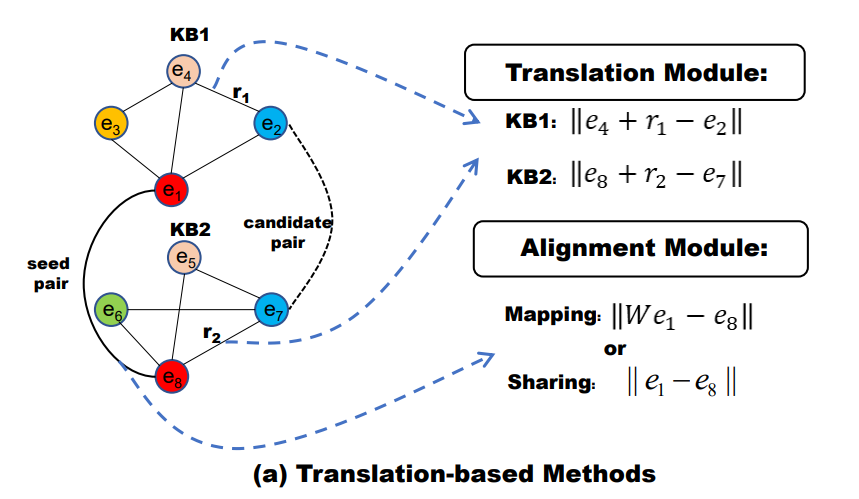
基于翻译（Translation-based）受跨语言word embedding任务的启发，这类方法假定不同的KG的embedding空间包含相似的分布，因此KGs之间的对齐实体在各自的向量空间中具有相似的位置特性。这类方法首先使用Trans-based KG embedding方法对各KG做单独的表示学习，得到各自的entity和relation向量表示，而后使用已知的（标注的）实体对齐将其投影到统一的向量空间中。

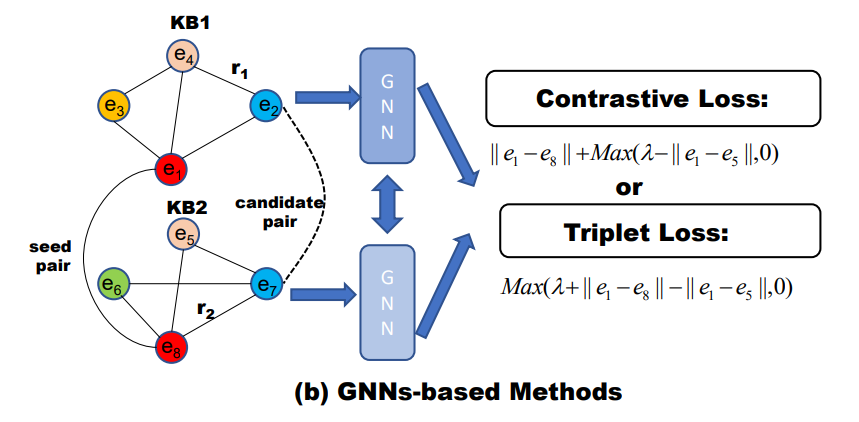
基于GNN（GNNs-based）不同于上述方法（relation作为实体之间的转换），GNNs通过邻居节点的集合（聚集）信息，生成节点级别的embedding。

 

对于上述两个问题的分析和猜想：

Q1. GNN最初是使用标准线性变换矩阵设计的，但是许多GNN-based将其约束为单位或者对角线。过去的方法都将其视为参数规约，但是并未就此做出解释和讨论。作者尝试在GCN-Align中删去这个设置时，模型性能在Hits@1上下降了10%，因此认为其中存在某些更加本质的问题；

Q2.许多任务中（比如链接预测）都需要KG模型，许多新的KG embeddings方法被提出并在这些任务上取得了不错的效果。但是在链接预测之类任务上效果出众的模型却没有在对齐任务上展现出显著的优势，过去的工作中仅给出了“并不是所有对于链接预测有效的模型都适用于实体对齐”，但并未给出进一步的分析。

为了进一步分析两者的原因，作者提出了一个抽象实体对齐框架，名为“Shape-Builder & Alignment”。在这个框架中，Trans-based与GNN-based方法均被视为各自设置下的特例。通过这个框架，作者成功找到了上述问题的答案：

A1. 实体对齐假定了两个（KG）分布具有相似性，所以为了避免结构性的破坏，在转换之后，实体的norms以及相对距离等信息应该保持不变，因此转换矩阵被强制为正交矩阵。

A2. 许多新的KG embedding方法都遵循了一个关键的idea-“将实体的embeddings转换为relation specific的版本”。然而他们的转换矩阵并不能服从正交属性，这就是实体对齐中这些方法效果不佳的原因。

因此作者提出两个实体对齐上理想转换操作的标准：1. Relation Differentiation；2. Dimensional Isometry；基于这两个标准，作者提出一种新的转换操作 “Relation Reflection Transformation”：该操作能够沿不同关系的超平面反映entity embeddings，从而用于构建relation specific entity embeddings. 这种反映矩阵（reflection matrix）是正交的，因此能够保证转换过程中的实体及其相对距离的不变性。（作者将该转换添加到GNN模型中，得到新的实体对齐方法RREA，relation reflection entity alignment）

Shape-Builder & Alignment

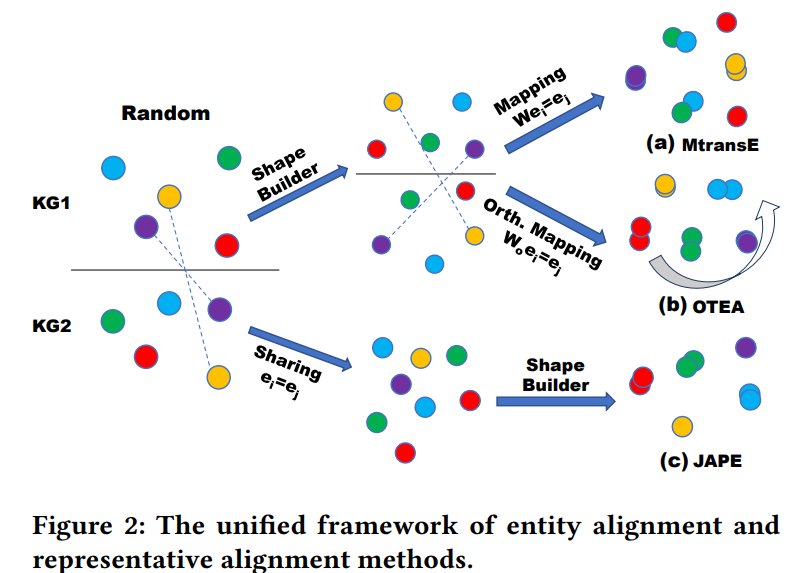
下图是作者提出的统一对齐框架的过程示意图：

Shape-Builder的主要函数是将随机初始化分布约束到一个特定的分布上（称之为shape）， 图2中的转换模型本质上就是shape-builder。这里的前置条件是“两个KG中获得的embeddings应当具有shape similarity”，即对等实体在向量空间中应该具有相似的相对位置。

Alignment 当shape similarity获得后，不同的shape可以通过标注的对齐实体所匹配。在图2中，映射就是对齐模型中所训练的转换矩阵W, 这个矩阵使得已标注数据差异尽可能小（通过以下公式：）

其中ei与ej是一对已知对齐，h表示对应实体的向量，为了保留转换中的不变性，W被约束为一个正交矩阵。

GNN-based方法在Shape-Builder & Alignment框架下的适用性分析：

基于GNN的实体对齐方法一般包括以下过程：

N表示实体e周围的邻，W则是l层的转换矩阵，公式2用于将实体邻居的信息聚合，而公式3用于将实体的embedding转换为一个更佳的版本。有许多的操作可以实现聚合的目的（例如normalized mean pooling或者attentional weighted summation）。

在得到embedding之后，GNN方法一般会构建如下损失使得对等实体更加接近对方，其中带有” ’ ”的为负例样本（随机替换正例样本中的实体得到）。

在AliNet中也有类似的损失函数：

可以看到，这类损失均可以拆分为两个部分：

1.对齐损失（正例）->框架中的alignment部分；

2.分离损失（负例）->框架中的shape-builder

为了进一步证明可用性，作者进行了可视化实验，在GNN-based方法作为shape-builder得到的分布中（使用AliNet），效果还是很清晰的。

为了衡量转换后向量分布的结构相似性，作者构建了一种相似性度量方法(带波浪线的实体来自某一KG，不带的来自另一KG，带有“ ’ ”的则为随机负例)：

实验数据

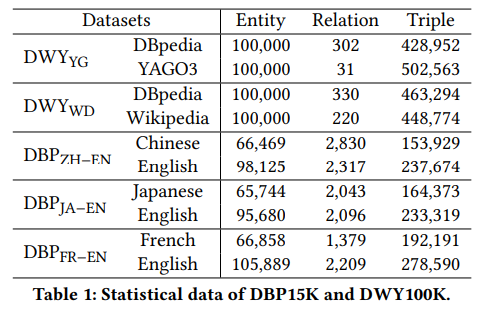
实验使用的语料是DWY100K及DBP15K，统计信息如下：

实验结果：

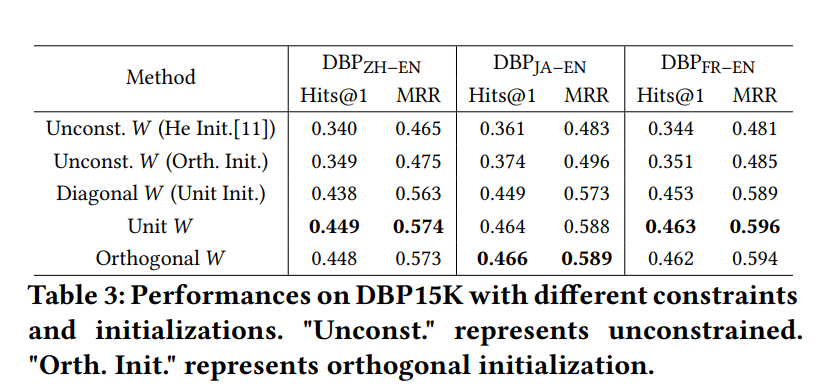
表3主要对比的是初始化时使用/不使用正交矩阵约束的情况下，模型的效果。

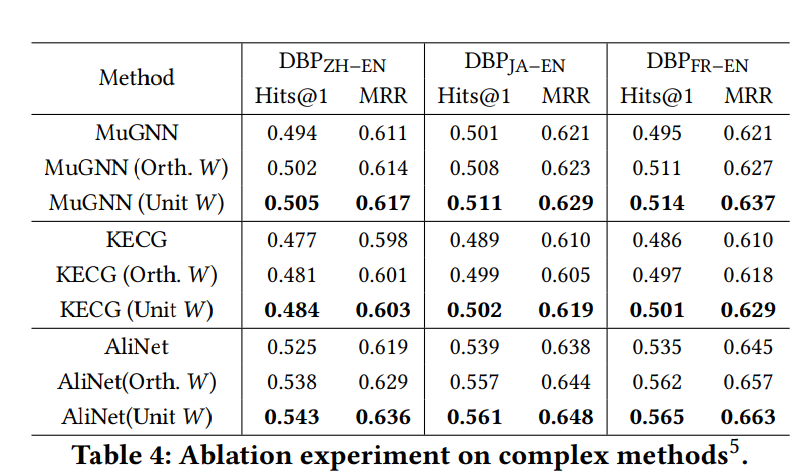
表4则是在不同GNN方法上的消融实验结果。

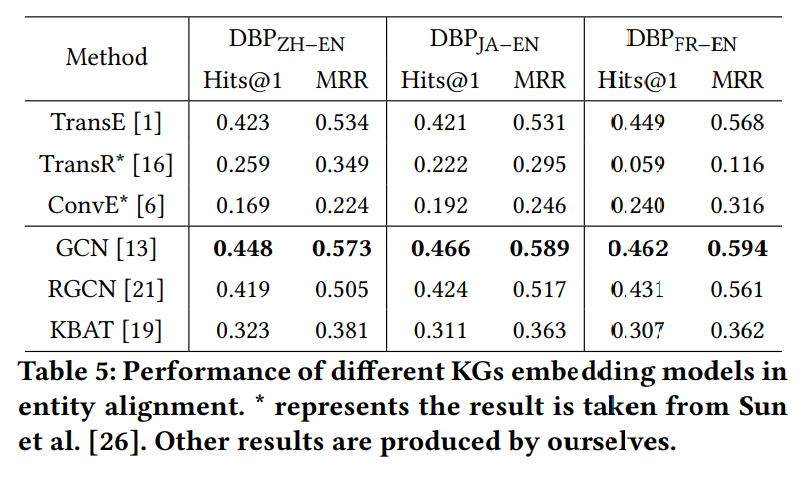
表5对比了该框架下不同KG embedding方法的效果差异性。

 

---

 

OpenKG

开放知识图谱（简称 OpenKG）旨在促进中文知识图谱数据的开放与互联，促进知识图谱和语义技术的普及和广泛应用。

点击阅读原文，进入 OpenKG 博客。