深入机器学习系列之:Gradient-boosted tree

导读
梯度提升属于Boost算法的一种,也可以说是Boost算法的一种改进,它与传统的Boost有着很大的区别,它的每一次计算都是为了减少上一次的残差,而为了减少这些残差,可以在残差减少的梯度方向上建立一个新模型。
来源: 星环科技
数据猿官网 | www.datayuan.cn

今日头条丨一点资讯丨腾讯丨搜狐丨网易丨凤凰丨阿里UC大鱼丨新浪微博丨新浪看点丨百度百家丨博客中国丨趣头条丨腾讯云·云+社区

梯度提升树
1
Boosting
Boosting是一类将弱学习器提升为强学习器的算法。这类算法的工作机制类似:先从初始训练集中训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注。 然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器的数目达到事先指定的值T,最终将这T个基学习器进行加权结合。
Boost算法是在算法开始时,为每一个样本赋上一个相等的权重值,也就是说,最开始的时候,大家都是一样重要的。 在每一次训练中得到的模型,会使得数据点的估计有所差异,所以在每一步结束后,我们需要对权重值进行处理,而处理的方式就是通过增加错分点的权重,这样使得某些点如果老是被分错,那么就会被“严重关注”,也就被赋上一个很高的权重。 然后等进行了N次迭代,将会得到N个简单的基分类器(basic learner),最后将它们组合起来,可以对它们进行加权(错误率越大的基分类器权重值越小,错误率越小的基分类器权重值越大)、或者让它们进行投票等得到一个最终的模型。
梯度提升(gradient boosting)属于Boost算法的一种,也可以说是Boost算法的一种改进,它与传统的Boost有着很大的区别,它的每一次计算都是为了减少上一次的残差(residual),而为了减少这些残差,可以在残差减少的梯度(Gradient)方向上建立一个新模型。所以说,在Gradient Boost中,每个新模型的建立是为了使得先前模型残差往梯度方向减少, 与传统的Boost算法对正确、错误的样本进行加权有着极大的区别。
梯度提升算法的核心在于,每棵树是从先前所有树的残差中来学习。利用的是当前模型中损失函数的负梯度值作为提升树算法中的残差的近似值,进而拟合一棵回归(分类)树。
2
梯度提升
根据参考文献【1】的介绍,梯度提升算法的算法流程如下所示:

在上述的流程中,F(x)表示学习器,psi表示损失函数,第3行的y_im表示负梯度方向,第4行的R_lm表示原数据改变分布后的数据。
在MLlib中,提供的损失函数有三种。如下图所示。

第一个对数损失用于分类,后两个平方误差和绝对误差用于回归。
3
随机梯度提升
有文献证明,注入随机性到上述的过程中可以提高函数估计的性能。受到Breiman的影响,将随机性作为一个考虑的因素。在每次迭代中,随机的在训练集中抽取一个子样本集,然后在后续的操作中用这个子样本集代替全体样本。 这就形成了随机梯度提升算法。它的流程如下所示:

4
实例
(提示:代码块部分可以左右滑动屏幕完整查看哦)
下面的代码是分类的例子:
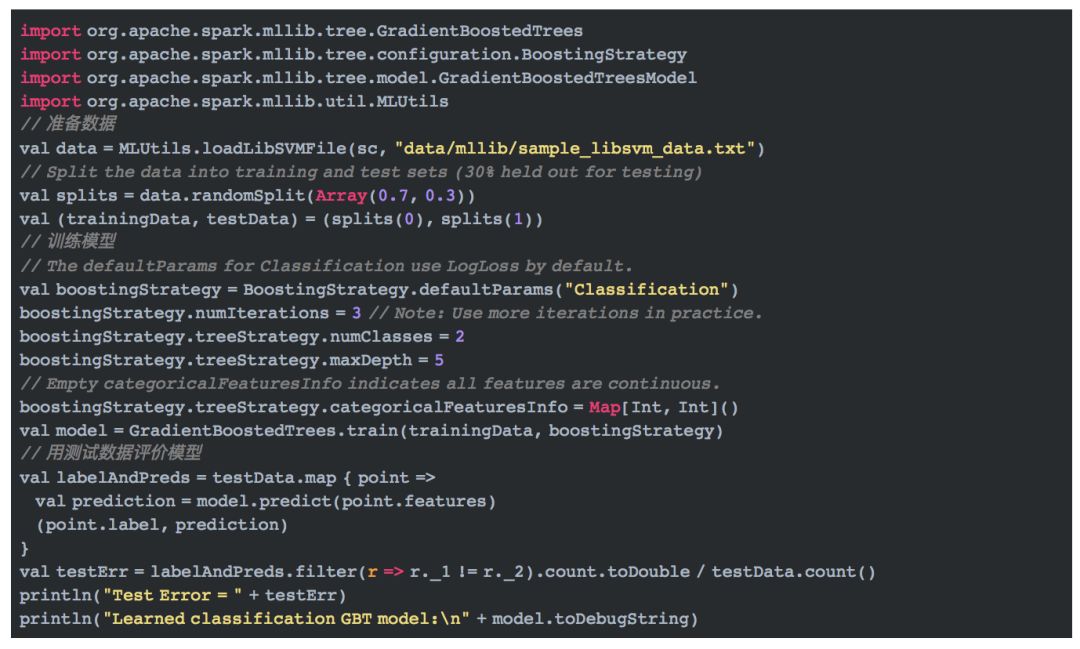
下面的代码是回归的例子:
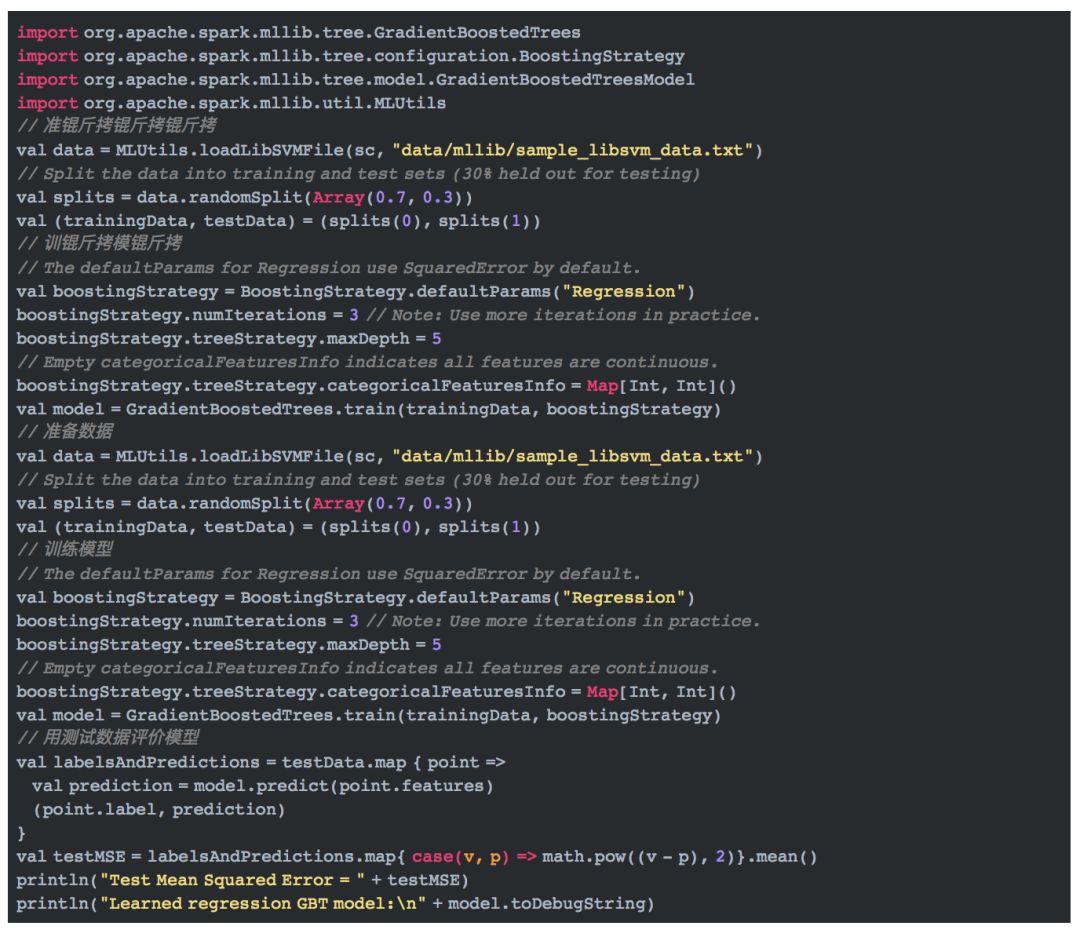
5
源码分析
5.1 训练分析
梯度提升树的训练从run方法开始。
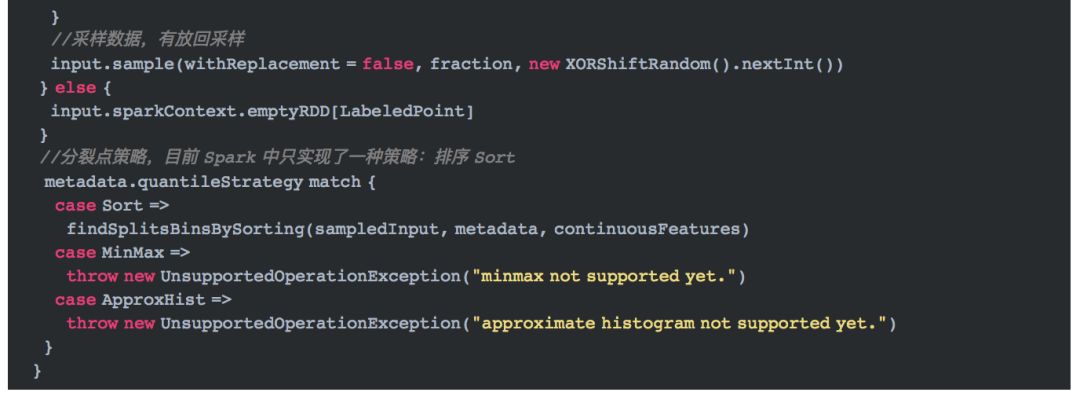
在MLlib中,梯度提升树只能用于二分类和回归。所以,在上面的代码中,将标签映射为-1,+1,那么二分类也可以被当做回归。整个训练过程在GradientBoostedTrees.boost中实现。 GradientBoostedTrees.boost的过程分为三步,第一步,初始化参数;第二步,训练第一棵树;第三步,迭代训练后续的树。下面分别介绍这三步。
-
初始化参数
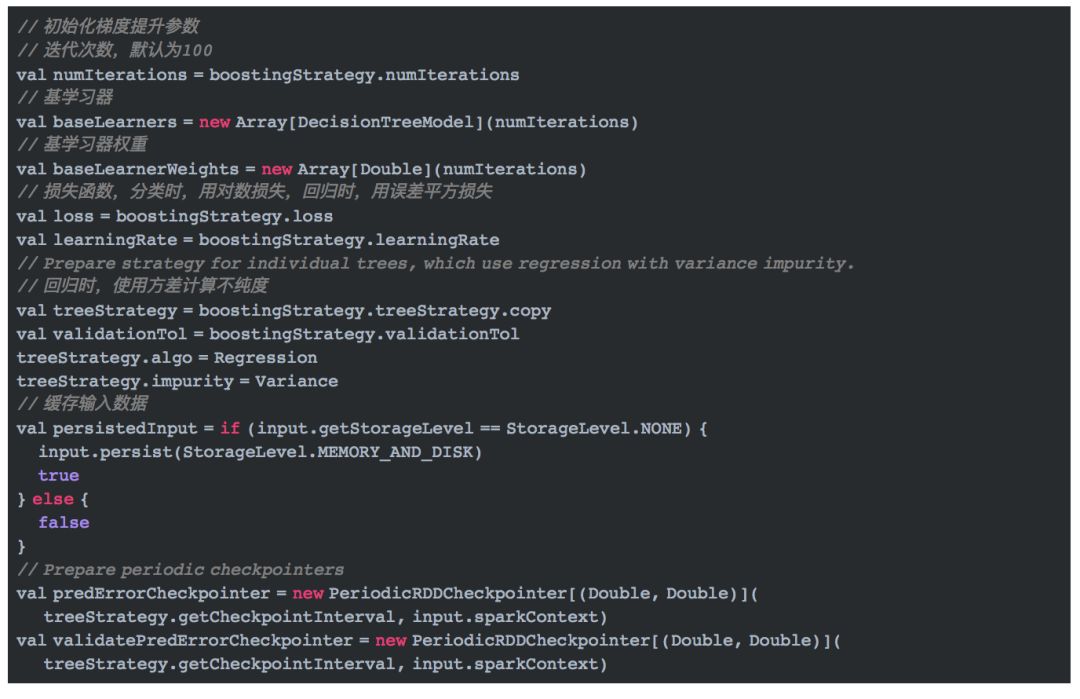
-
训练第一棵树(即第一个基学习器)

这里比较关键的是通过GradientBoostedTreesModel.computeInitialPredictionAndError计算初始的预测和误差。

根据选择的损失函数的不同,computeError的实现不同。

-
迭代训练后续树
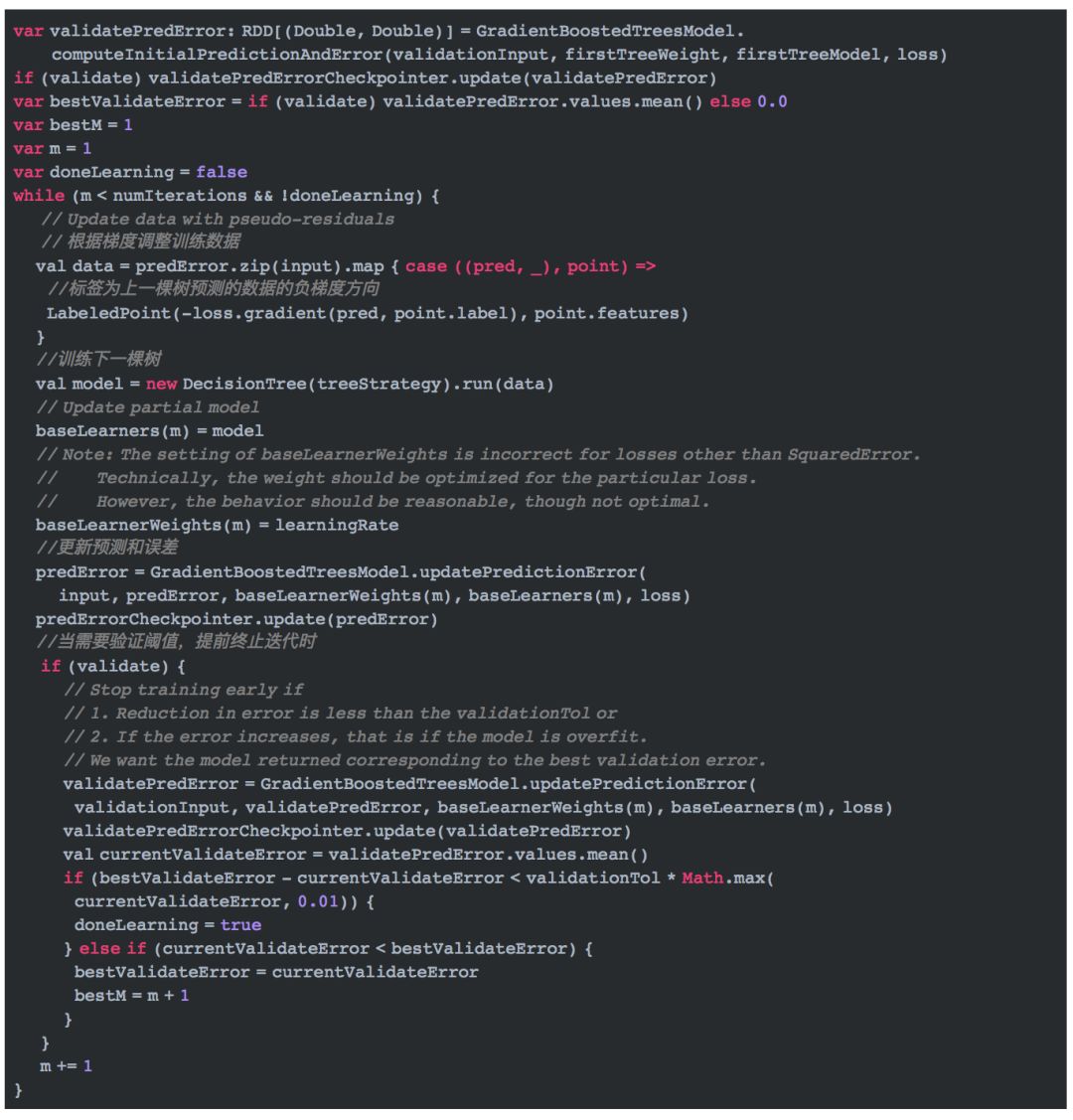
上面代码最重要的部分是更新预测和误差的实现。通过GradientBoostedTreesModel.updatePredictionError实现。

5.2 测试
利用梯度提升树进行预测时,调用的predict方法扩展自TreeEnsembleModel,它是树结构组合模型的表示,其核心代码如下所示: