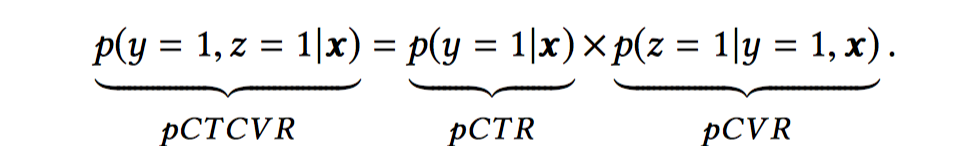SIGIR2022 | ESCM^2: 升级版全空间多任务转化率预估

2022 年 6 月 10 日 机器学习与推荐算法

今天分享阿里巴巴-蚂蚁发表在SIGIR2022的论文：ESCM^2 : Entire Space Counterfactual Multi-Task Model for Post-Click Conversion Rate Estimation ^[1]。值得一读的工作，看起来推导很多，但对于加强理解样本偏差/优化空间等概念以及提升多任务模型应用有很好的帮助。

ESCM^2在ESMM基础上做了升级，提出了一种新的CVR预估模型，即：全空间反事实多任务模型，借助因果推断来解决ESMM中存在的预估有偏和独立性先验这两大问题。其中，预估有偏(IEB，Inherent Estimation Bias)是指ESMM预估的CVR天然比ground truth的CVR要大；独立性先验(PIP，Potential Independence Priority)是指ESMM在建模CTCVR时，会忽视"转化"依赖于"点击"这一因果关系。因此提出了，利用因果推断中的反事实经验最小化作为正则项来同时解决IEB和PIP问题。在/离线实验表明模型不仅能解决这两大类问题，指标上也显著优于其他基线模型。

1. 背景：ESMM

先介绍下背景 (对ESMM熟悉的同学可以跳过这个Part)。

ESCM^2是阿里巴巴蚂蚁团队的工作，是要解决ESMM中存在的问题。而ESMM是曾经阿里妈妈朱小强/盖坤团队发表在SIGIR2018的论文^[2]，属于两个团队的工作。

ESMM

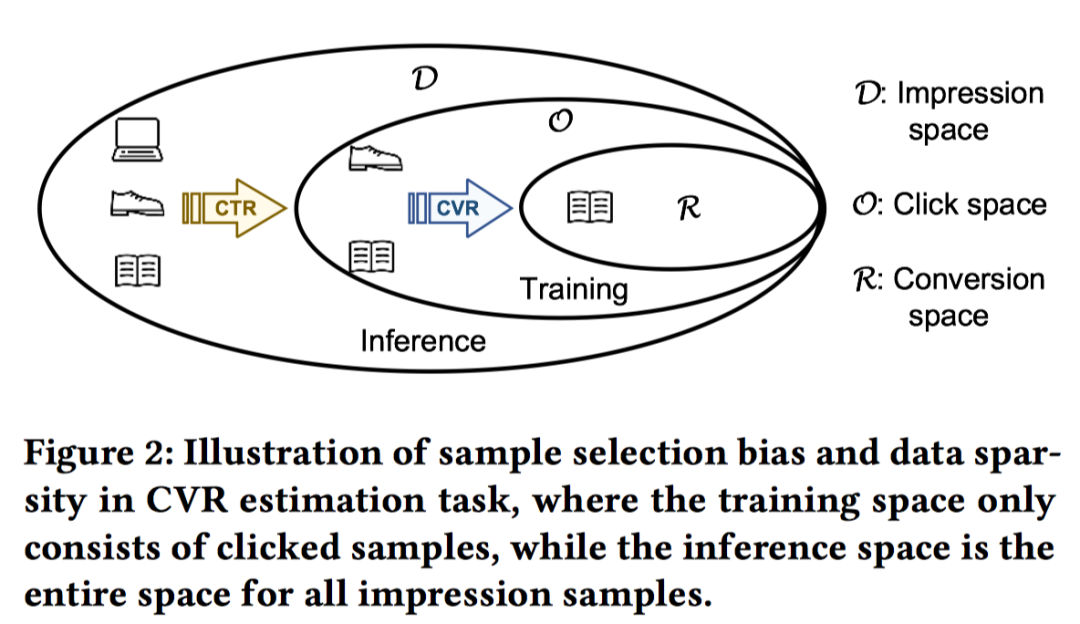
ESMM基于多任务学习的思路，提出一种新的CVR预估模型，有效解决了真实场景中CVR预估面临的数据稀疏(Data Sparsity, DS)以及样本选择偏差(Sample Selection Bias, SSB)这两个关键问题^[3]。其中，DS是指作为CVR训练数据的点击样本远小于CTR预估训练使用的曝光样本；SSB是指，传统CVR离线建模时以点击空间的样本为训练集，其中点击未转化为负例，点击并转化为正例；在线预估时又是对全样本空间进行预估，二者存在Diff，即：训练数据与实际要预测的数据来自不同分布，在点击空间上训练得到的CVR预估值不是全样本空间上的无偏估计。

SSB

ESMM从要预估的CTR(点击率)、CVR(转化率)、CTCVR(点击然后转化率)三者的关系入手，

其中是转化label，是点击label。可以看到pCTR和pCTCVR预估的空间都是全样本空间，PCVR预估的空间是点击空间。那么可以通过在全样本空间建模pCTR和pCTCVR多目标，从而隐式地建模pCVR (pCVR=pCTCVR/pCTR)。

ESMM

主任务是pCVR任务，辅助任务包括两个部分，pCTR以及PCTCVR。隐式学习pCVR是指这里pCVR（粉色节点）仅是网络中的一个variable，没有显式的监督信号来引导学习。模型的损失函数是用于学习pCTR和PCTCVR的。

值得一提的是，此后涌现出了ESM^2^[10]模型，是ESMM的升级版，但大体框架和上面一样。

2. Motivation

ESMM模型乍一看很合理，确实是开创性的思路。但深究后会发现存在两大类问题(IEB和PIP)，也是ESCM^2的研究动机所在。

不过在ESCM^2在诞生之前，还得先看另外一篇文章，"Large-scale causal approaches to debiasing post-click conversion rate estimation with multi-task learning"^[5]，发表在WWW2020。

这个工作是ESM^2团队的工作(和ESM^2的作者有交叉)。是这篇文章第一次指出ESMM存在预估偏差问题，即开篇提到的ESMM预估的CVR天然比ground truth的CVR要大。并提出了利用因果推断中的IPW (Inverse Propensity Weighting)和DR(Doubly Robust Estimator)手段来纠偏。

ESCM^2也引用了这篇文章，同样从因果推断角度，利用IPW和DR来解决。两篇文章方法很相近，两类问题在WWW2020这篇文章中实际上也涉及到。按照我的理解，SIGIR2022这篇文章借鉴了不少WWW2020文章的思路和方法，在这个基础上做了一些完善，比如在证明ESMM有偏时，WWW20的证明方法不够solid，SIGIR22做了完善；网络结构和学习目标上也有做一些调整等。

抛开这些因素，我们来重点聊聊ESCM^2这篇文章的内容。

ESCM^2指出ESMM存在两大类问题：

预估有偏(IEB， Inherent Estimation Bias)是指ESMM预估的CVR天然比ground truth的CVR要大，会在下文进行证明；
独立性先验(PIP， Potential Independence Priority)是指ESMM分别建模CTR和CVR，会忽视" 转化"依赖于" 点击"这一因果关系，即：模型结构上CVR的预测是不依赖于click的，但真实情况是发生点击后，才会发生转化，是有依赖关系的，导致CTCVR预估不准。

因此文章的核心贡献在于：

提出了ESMM存在上述两大类问题，IEB和PIP。
提出了从 因果推断角度，利用IPW和DR手段来进行多目标学习，来解决这两大类问题。
离线和在线实验表明了ESCM^2方法的有效性。

3. Discussion: ESMM

这个部分介绍如何证明ESMM存在IEB和PIP两大类问题。这部分证明不做重点介绍，感兴趣的可以看原文。结论就是：

结论1：ESMM中左侧CVR main task是有偏的，且总是大于真实值，即：，预估值和真实值在曝光空间上的偏差大于0。这个结论的根源在于ESMM在曝光空间来优化CVR，和真实情况有悖，真实情况下转化必须依赖于点击，先点击才有转化。作者认为还是要在点击空间来优化CVR，但要做的是在点击空间优化时直接解决SSB问题，消除Bias。即使是在点击空间做优化，也能够做到全样本空间下CVR真实值的无偏估计。
结论2：ESMM的左侧的CVR main task是有偏的，其预估的是，忽视了对点击的依赖，而不是真实情况下的这会导致CTCVR的预估存在问题。真实情况下，根据链式法则，有：

由于ESMM忽视了转化对点击的依赖关系，会造成。显然是有问题。

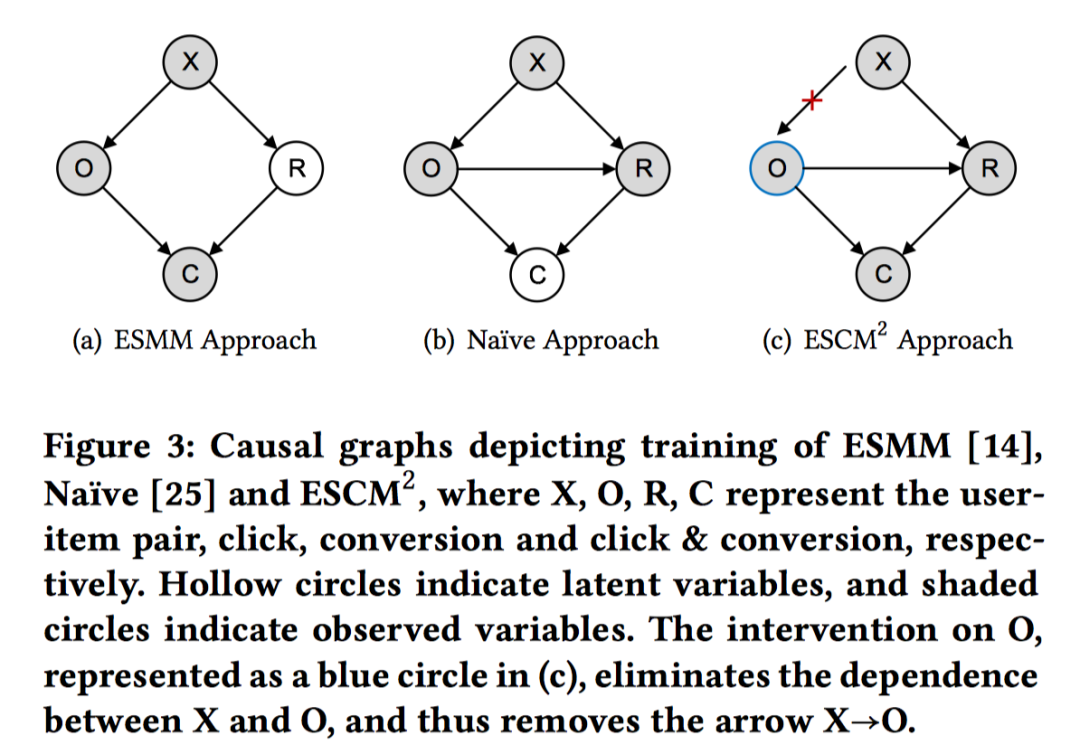
从因果图角度来理解全样本空间(X)、点击(O)、转化(R)、点击&转化(C)的关系。如下图所示：

按照我的理解，X可以理解为全样本空间，不仅仅是曝光空间，因为曝光空间本身就是有偏的。但是CVR或者CTR模型一般在曝光空间上进行优化，所以忽略这些因素，X可以近似理解为曝光空间。

(b)是传统的方法，在点击样本上进行CVR预估。此时，点击O依赖于X、R转化依赖于X和点击O、C点击&转化依赖于O和R。
(a) 是ESMM的方法，R的预估不依赖于O，即：main task CVR的预估的是，没有conditioned on 。
(c)是ESCM^2的方法，去掉了X到O之间的绝对依赖关系。这个O和a,b中的O是有差异的，用蓝色的圈表示，即：do(O)。对于真实点击样本，do(O)=O即为真实点击，X确实是依赖于O；而对于未点击样本，需要结合因果推断-反事实推理方法，假设用户点击了这个样本，有多大可能这个样本会转化？do是do-calculus，源自Judea Pearl’s Do-Calculus^[6]的思路，可以理解为因果推理中的干预机制。

这个部分怎么理解呢？我们可以从全样本空间开始理解。我们知道CTR预估模型一般在曝光空间进行优化，当曝光不是随机的时候，CTR预估值很可能不是真实CTR的无偏估计，此时引入曝光的倾向性(IPW)作为损失函数中的样本权重时，可以解决这种偏差，相当于低曝光倾向的item反而被点击了，那么其权重应该更高，基于IPW学习到的CTR预估值是全样本空间真实CTR的无偏估计。

同理，如何实现全样本空间真实CVR的无偏估计呢？首先CVR一定是依赖于点击的，有了点击才会转化，因此可以直接在点击空间进行优化。但其实每个点击sample的倾向性是不一样的。传统的方法直接在点击空间进行CVR预估，不考虑这种倾向性，此时CVR预估值不是全样本空间真实CVR的无偏估计。倘若能考虑每个点击sample的倾向性，同样基于IPW的方法，对点击sample进行加权，就能够实现在点击空间直接优化CVR预估，且这个预估结果是全样本空间真实CVR的无偏估计。

4. Solution

有了上面的基础，我们来介绍ESCM^2提出的反事实风险正则项以及模型整体的架构。

4.1 Counterfactual Risk Regularizer

引入inverse propensity score(IPS)作为点击sample的权重，得到新的学习目标：

其中，是点击label，只在等于1的时候对上述损失有影响，也即是在点击样本空间进行优化的。是真实转化label和预估CVR之间的差异，采用的是交叉熵损失，后续会简写为。

即用户点击item 的概率，衡量了点击倾向。点击倾向越小，却最终发生了转化，那么显然这个样本的权重应该更大。真实的通常无法获取，因此通过预估值来替代。可以很容易证明只要够准确，上述损失函数是真实CVR的无偏估计。显然，CTR预估结果是的不二选择。

但IPS的问题在于方差很大，一旦不准，上述预估就可能不准确，为了解决样本权重过度依赖倾向得分准确性的问题，又有了新的方法Doubly Robust Estimator^[7](DR，双鲁棒模型)，类似于鸡蛋不放在一个篮子里的投资方法，它结合倾向得分和结果回归模型来得到样本权重，只要二者有一个是对的，结果就是无偏的。可以参考^[8]中的解读，

这里面引入了1个新的概念error deviation：，中文可以称为误差的偏差。其中为真实预估误差，是Imputation error填充偏差，即预估误差的估计值(重要概念)，通过回归拟合真实预估误差来弥补IPW不够准确时的问题。Imputation error可以和IPS融合起来形成DR方法，推导出优化目标如下：

和任意一者是无偏时，整体CVR预估就是无偏的，因此鲁棒性更好。

把各个式子代入后，可以发现这里头有三个要预估的变量，戴着帽子，分别是：

中的 CVR预估值 ，即：在点击空间进行建模CVR预估。
点击倾向预估，即：在全样本空间进行CTR预估。
填充偏差预估，即：在全样本空间进行CVR预估误差的预估。（比较拗口）

因此，在DR方法中，模型预估架构可以预见是有3个组成部分。可以证明上述和是CVR的无偏估计，因此可以解决开篇提到的IEB问题，具体证明感兴趣可以参见原文；由于在点击空间进行CVR优化，因此可以解决PIP问题。

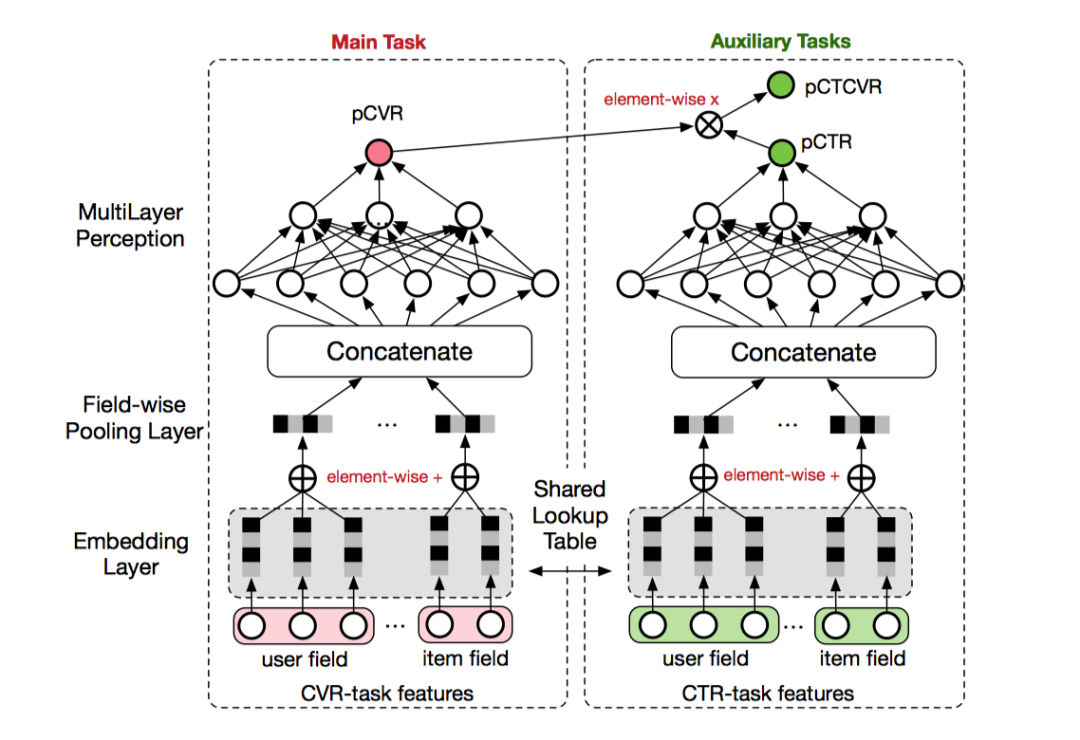
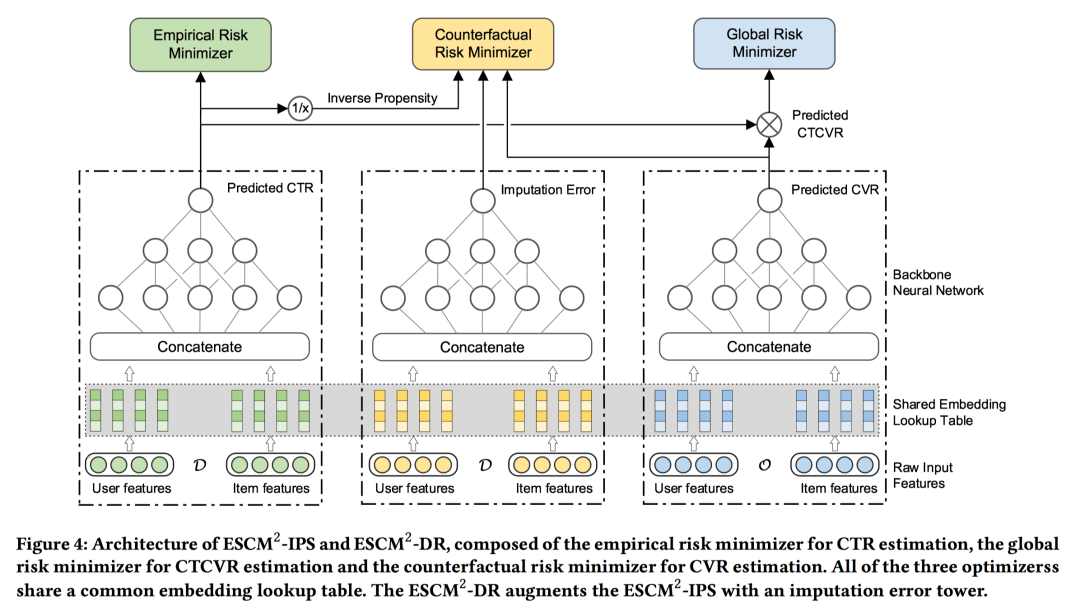
4.2 Architecture of ESCM^2

整体的模型架构如下图所示：如上述所预见的，基于DR方法的模型包括3个部分。

最左侧是在 全空间进行 CTR预估，网络参数记做，用于最小化经验风险损失；CTR预估值会作为点击倾向分输入到反事实CVR损失中，也会用于CTCVR的计算；
中间是在 全空间进行 填充误差预估，网络参数记做，用于DR方法中来最小化反事实风险损失，在全样本空间进行CVR预估误差的预估，IPS方法中不需要该塔；
最右侧是在 点击空间进行 CVR预估，网络参数记做，用于优化反事实CVR损失和CTCVR损失优化。

模型架构

下面介绍模型的学习损失函数。基础损失和ESMM一样，包括了CTR损失、CTCVR损失。但要注意后者CTCVR是在点击空间进行优化，而ESMM是在全样本空间进行优化(更稀疏)，二者有着本质的区别。除此之外，ESCM^2引入了上一节提到的CVR反事实损失作为损失项。采用IPS时，；采用DR时，。因此，最终的损失为：

要关注不同损失项使用的训练样本是不一样的。由于是全样本空间CVR的无偏估计，因此在线上推理阶段可以适用于全样本空间。

在全样本空间上进行优化，对应Empirical Risk Minimizer；
和都只在点击空间进行优化，分别对应于Counterfactual Risk Minimizer和Global Risk Minimizer。通过反事实IPS和DR能够使得在点击空间优化CVR是全样本空间真实CVR的无偏估计，和ESMM思想有本质的差别。

但这里本人比较疑惑的是，CVR已经是无偏估计了，CTCVR项其实可以不需要进行建模了。个人理解可能CTCVR在真实场景下是个很重要的指标，是精排得分的核心组成部分，因此也单独进行建模，实际效果也会更好。

的形式，代入上述各个网络的参数如下，可得：

IPS：。看起来很复杂，其实很好理解。代表点击样本才会起作用，即在点击空间进行优化。分子是真实的转化label 和第三个网络输出的 CVR预估值 的交叉熵损失；分母是点击的倾向，通过第一个网络输出 CTR预估值 来表示。整体的网络参数就是 第一个CTR塔和 第三个CVR塔的参数。
DR：，其中，通过第二个网络输出IMP 填充误差预估值；依赖于第二个网络填充误差预估值和CVR预估真实误差的差值。为了保证填充误差预估的准确性，可以最小化，使用平方损失。最终, 。整体的网络参数就是 第一个CTR塔、 第二个IMP塔和 第三个CVR塔的参数。

不得不说NN是万能的，通过NN来建模各种复杂推导而来的预估模型真的方便！

5.Evaluation

读论文最精彩的地方除了模型部分之外，就是实验评估部分了，这篇文章的实验部分也是相当精彩，信息量巨大，值得一读。

5.1 Dataset

使用的数据集包括真实的数据集以及公开的数据集。

真实数据集是离线90天的数据，下采样后的imp:click:conversion=100：10：1，按照时间顺序来构造训练集/验证集/测试集。
公开数据集采用的是Ali-CCP(Alibaba Click and Conversion Prediction)，hold-out 10%数据做验证集。

5.2 Competitors

对比的基线方法包括，耳熟能详的就不加引用了。

Naive(MMoE)，除了CTR预估外，另一个任务在点击空间进行CVR预估。
MTL-IMP(PLE)，和Naive方法类似，只不过 未点击的样本也作为CVR预估的负样本。
ESMM ^[2] ：包括最早的ESMM以及升级版ESM^2。
MTL-EIB ^[9]：Error Imputation方法，猜测类似前文的DR方法。
MTL-IPS ^[5]：WWW2020的方法，和本文很像的一篇工作。
MTL-DR ^[5]：WWW2020的方法，和本文很像的一篇工作。
ESCM^2-IPS：本文工作，使用IPS方法。
ESCM^2-DR：本文工作，使用DR方法。

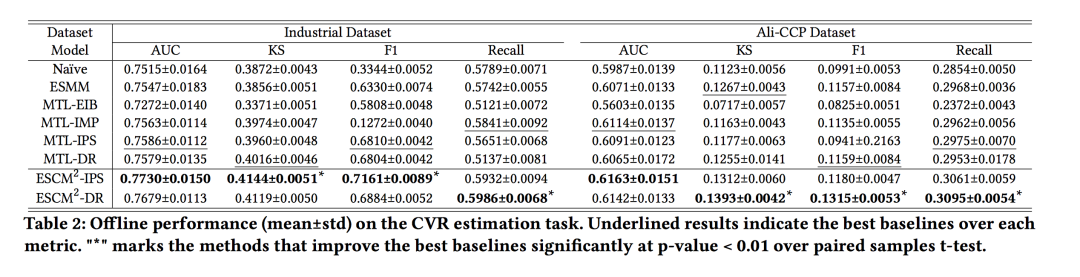
指标采用的AUC,F1,还有个KS模型区分度指标(没有细看)，CVR的对比结果如下，还是很亮眼的。

CVR AUC等指标评估

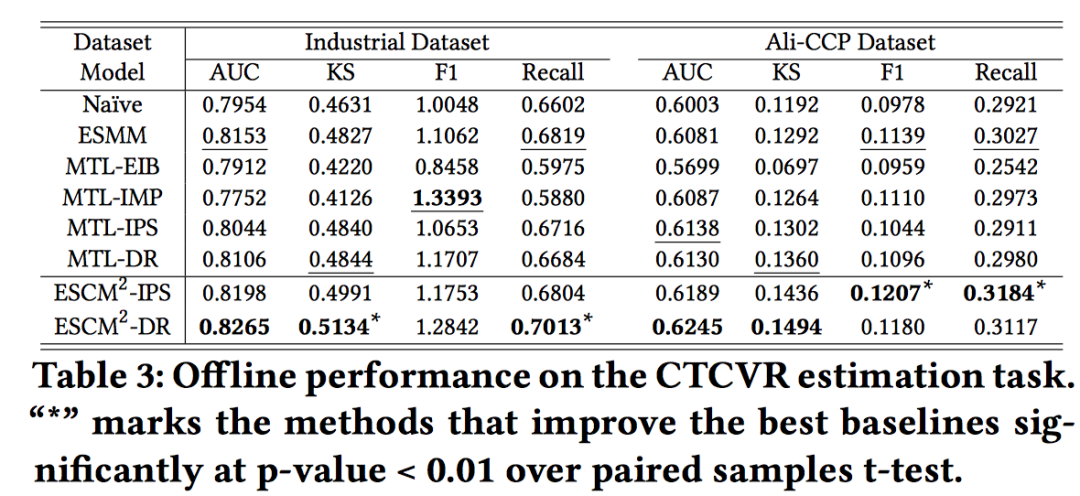
作者还做了CTCVR的对比，整体而言ESCM^2还是最好的。其实还可以稍微看一下CTR AUC指标，但是作者没有放。

CTCVR AUC等指标评估

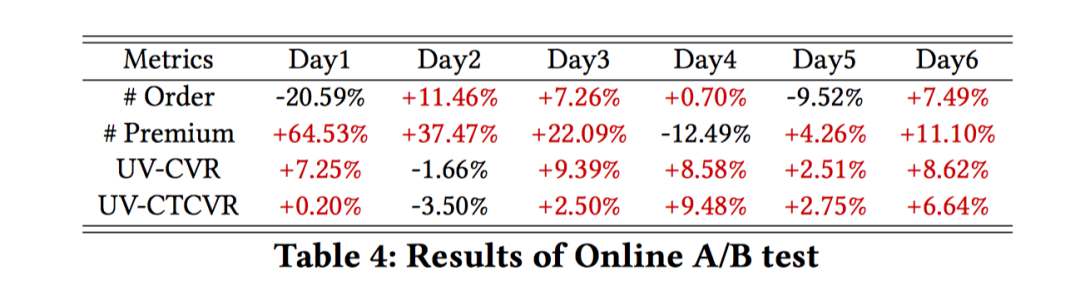
5.3 Online A/B Test

应用在3种场景，主场景、新场景、广告联盟等，都取得了显著收益，比如：主场景6天明细收益如下：

5.4 Discussion on IEB and PIP

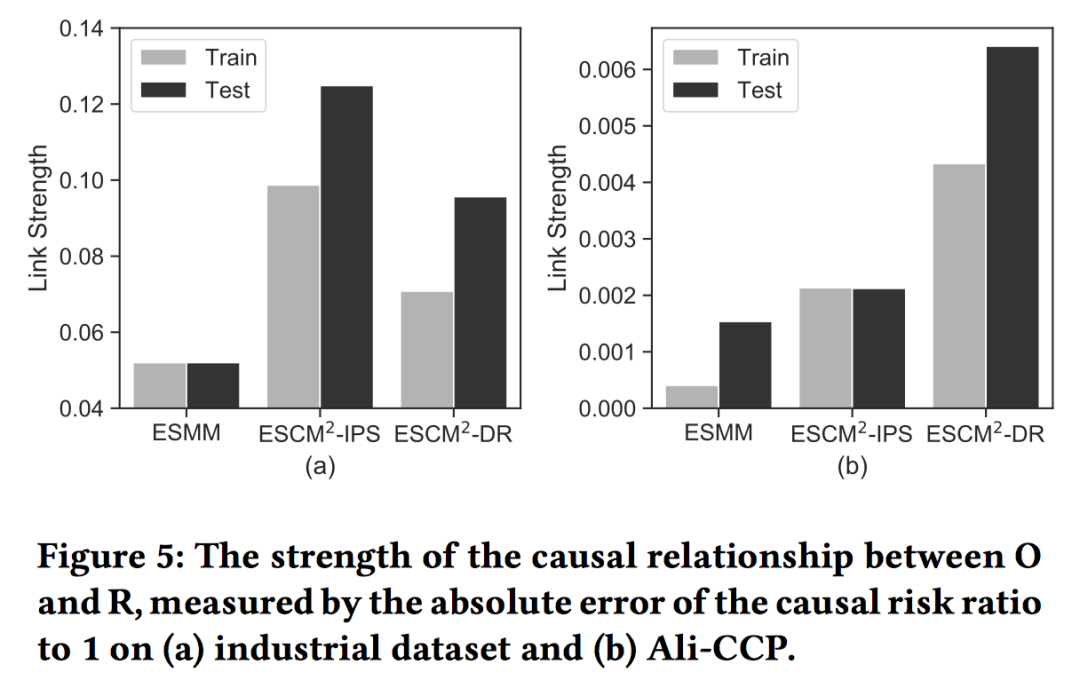
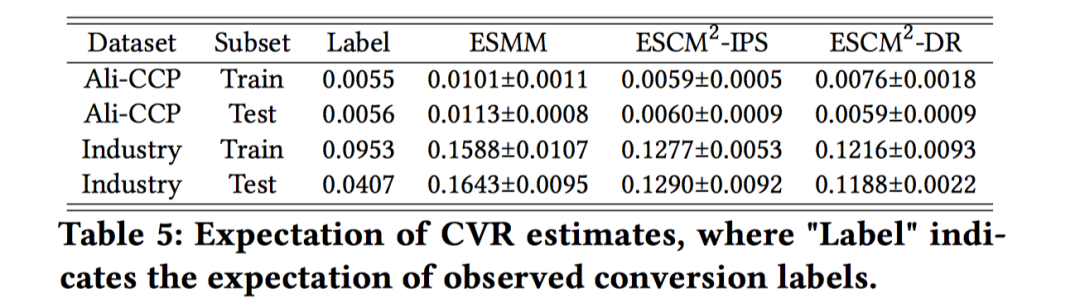
首先是IEB问题，目标是看看不同的CVR预估模型的预估偏差如何。首先计算点击空间下的观测转化label的期望(sum(conversion-label)/sum(click-label))，可以看做是全样本空间下真实CVR期望的上界(很好理解，点击到转化的概率肯定大于曝光到转化的概率)，用于近似真实CVR；接着计算各个CVR模型在曝光空间上的pCVR均值；对比这个真实CVR和pCVR均值的差，差值越小说明越接近无偏。如下图所示，ESCM^2更接近无偏。

接着是PIP问题，PIP根源在于ESMM忽视了点击到转化的因果关系，但这个因果关系的强度很难量化出来。作者采用了propensity score matching (PSM)模型来消除confounder因素，再计算Causal risk ratio (CRR)来量化。具体的可参见原文。总之可以量化出ESCM^2能更好的建模click-conversion的依赖关系。

5.5 Parameter Sensitivity and Ablation Study

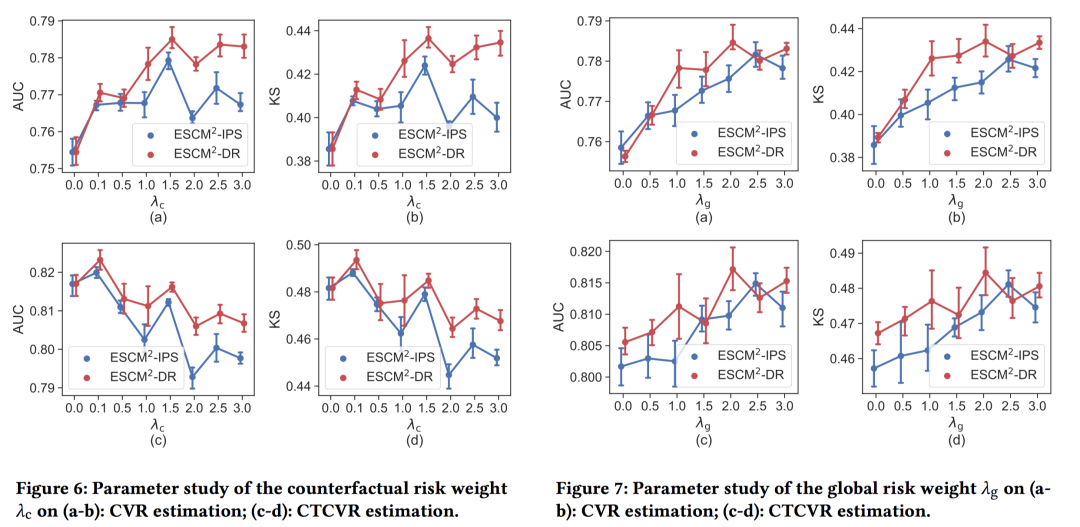
第一幅图是CVR损失项的系数，系数越大，a-b图的CVR预估越准，(c,d)的CTCVR预估先上升后显著下降，主要是因为会影响CTR的预估，导致CTCVR预估能力下降。因此作者强调应该位于[0,0,0.1]之间。

第二幅图是CTCVT损失项的系数，在[0,3.0]之间调参，可以看到随着系数的增大,CVR和CTCVR都先显著增长，而后开始下降。

损失函数项系数

6.Conclusion

这篇文章笔者阅读了好几遍，刚开始确实不好一下子读懂，但读明白后发现理论证明过程挺复杂，但最终用多任务DNN进行建模时，实际上很优雅简洁，实现上其实也不复杂，有“Best Paper”的潜质。

到此，ESMM相关的工作脉络可以做个梳理：

ESMM^[ ^2]：最早的工作，阿里妈妈团队朱小强盖坤团队提出的，发表在SIGIR2018；
ESM^2 ^[10]：ESMM的升级版，姐妹篇，是阿里另一个团队的工作，进一步解决ESMM中的DS问题，发表在SIGIR2020；
Multi-DR, Multi-IPW ^[5]：出自ESM^2的团队，首次揭露ESMM预估有偏，并引入因果推断的方法来解决ESMM预估有偏的问题，发表在WWW2020；
ESCM^2 ^[1]：出自阿里蚂蚁团队，在Multi-DR, Multi-IPW基础上做了更solid的证明，模型优化部分也做了一些调整，发表在SIGIR2022。

还有个有趣的事情，笔者发现这篇文章在目前关于SIGIR2022的文章整理^[4]里没有出现，不知道是整理的人漏掉了，还是后来加到Accepted Papers。总之，个人觉得是好文章，理论严谨，结果优雅，在多任务学习、CVR预估等场景值得一试。

最后，有解读不对的地方欢迎多多指教。

References

[1] Wang H, Chang T W, Liu T, et al. ESCM : Entire Space Counterfactual Multi-Task Model for Post-Click Conversion Rate Estimation[J]. arXiv preprint arXiv:2204.05125, 2022.

[2] Xiao Ma, Liqin Zhao, Guan Huang, Zhi Wang, Zelin Hu, Xiaoqiang Zhu, and Kun Gai. 2018. Entire Space Multi-Task Model: An Effective Approach for Estimating Post-Click Conversion Rate. In SIGIR. 1137–1140.

[3] 阿里CVR预估模型之ESMM，https://zhuanlan.zhihu.com/p/57481330

[4] SIGIR2022论文整理，https://zhuanlan.zhihu.com/p/368966327

[5] Wenhao Zhang, Wentian Bao, Xiao-Yang Liu, Keping Yang, Quan Lin, Hong Wen, and Ramin Ramezani. 2020. Large-scale Causal Approaches to Debiasing Post-click Conversion Rate Estimation with Multi-task Learning. In WWW. 2775278

[6] Introduction to Judea Pearl’s Do-Calculus: https://arxiv.org/pdf/1305.5506.pdf

[7] Xiaojie Wang, Rui Zhang, Yu Sun, and Jianzhong Qi. 2019. Doubly Robust Joint Learning for Recommendation on Data Missing Not at Random. In ICML

[8] ICML2019 面向推荐系统的双鲁棒联合学习：https://zhuanlan.zhihu.com/p/47534876

[9] Harald Steck. 2010. Training and testing of recommender systems on data missing not at random. In SIGKDD. 713–722.

[10] Wen H, Zhang J, Wang Y, et al. Entire space multi-task modeling via post-click behavior decomposition for conversion rate prediction. SIGKDD. 2020: 2377-2386.