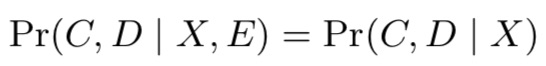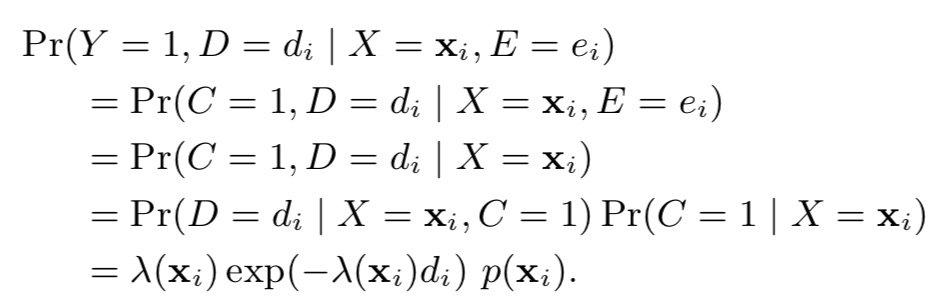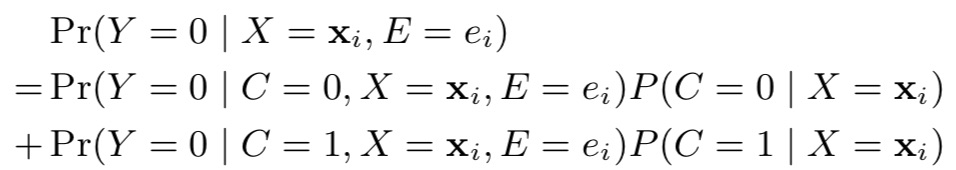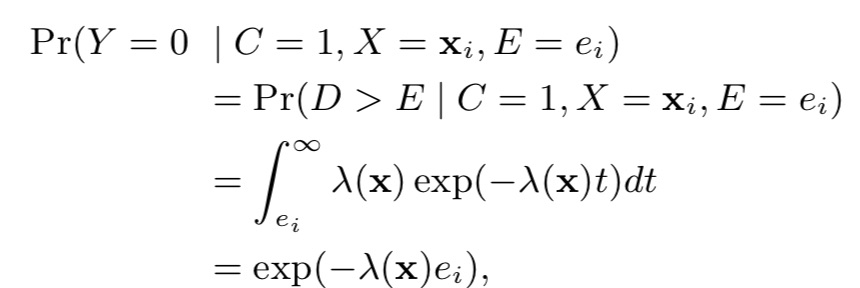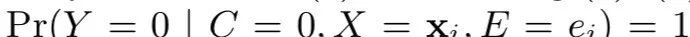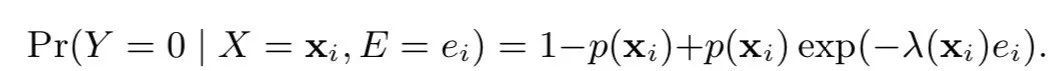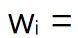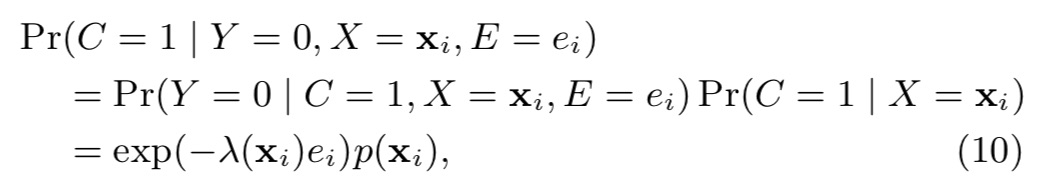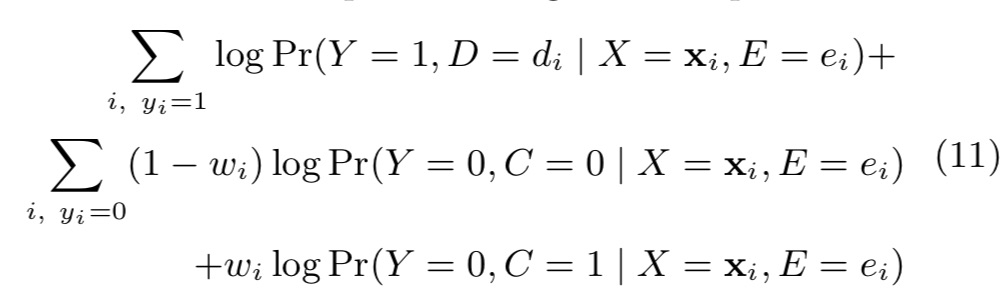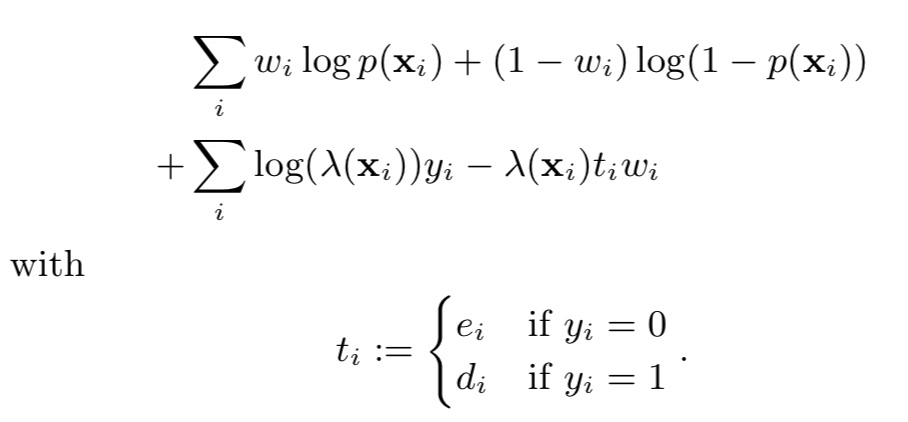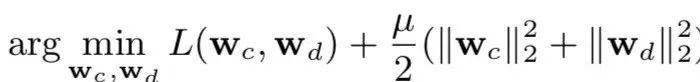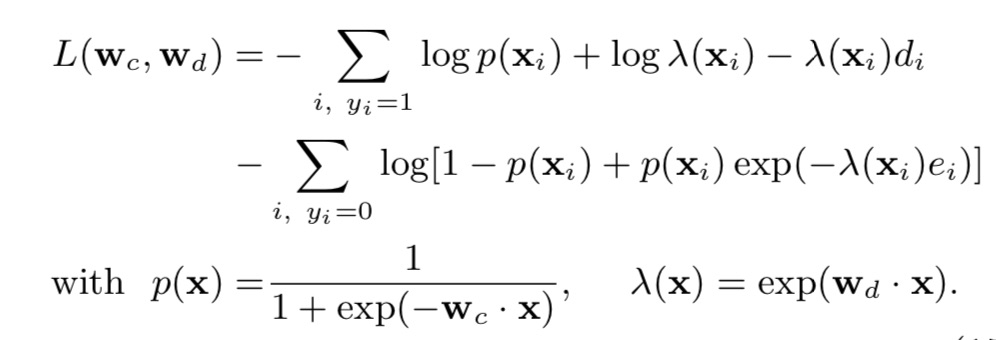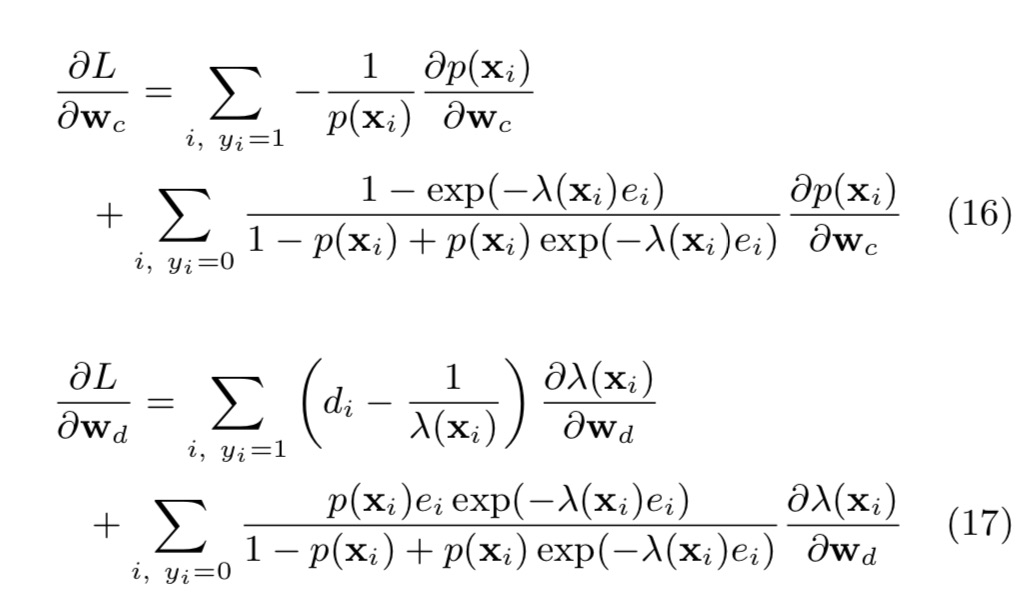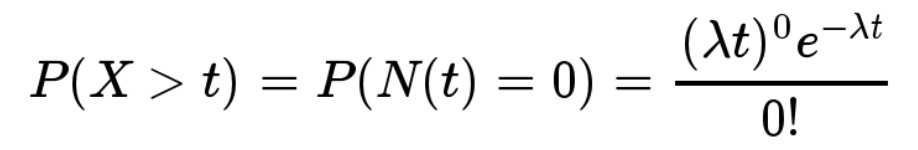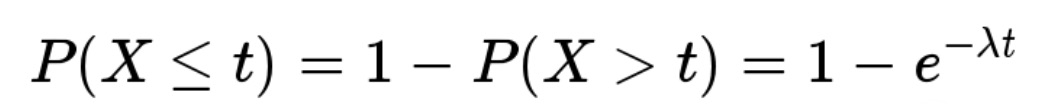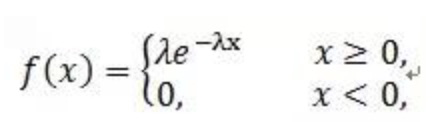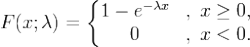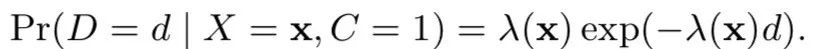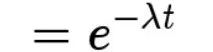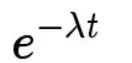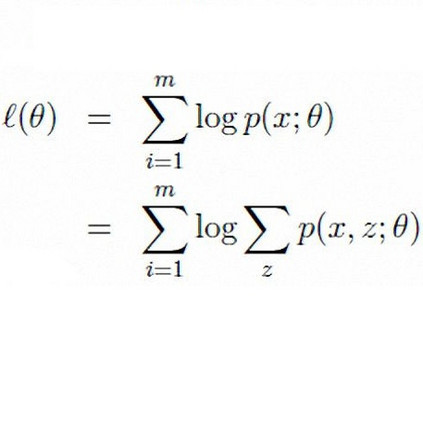转化率预估(pCVR)系列--延迟预估模型（上篇）

说到cvr延迟预估，不得不提开山之作“Modeling Delayed Feedback in Display Advertising”，本文从这篇经典论文入手，对cvr预估中遇到的订单延迟问题的背景、影响及解决方案进行了详细讲解。

本文关键内容总结如下：

1.CVR建模拆解：将cvr预估拆分为两个模型，转化模型（conversion model，CVR）和订单延迟模型（Delayed Feedback Model，DFM）。CVR模型用户预估用户最终是否发生转化，DFM则预估点击后第几天发生转化。

2. DFM的优化思路：假设转化延迟时间服从指数分布。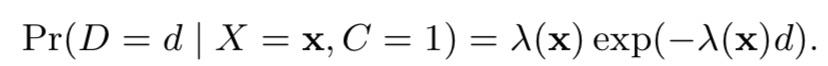

3.模型训练及预估：CVR和DFM联合训练，采用EM算法或sgd-Joint Learning等方法。在线预估时，只使用CVR模型，DFM被舍弃。

背景

展示广告中，oCPX/CPA模式（eCPM=pCTR * pCVR * CPA）下pcvr预估的准确性至关重要。

在参考ctr模型优化经验优化cvr模型时，会遇到一个问题，与点击（相比曝光）发生时间相比，转化发生时间要晚的多，很多时候转化事件会发生在广告被点击的几天（甚至一周）后。

转化延迟会对模型的训练产生负向的影响，通常简单的做法，就是预先设定好转化归因的时间窗口（例如15天），并且cvr模型只使用已归因完全（已超过归因时间窗口）的数据进行模型训练（例如，只使用15天之前的数据）。这种情况下，归因时间窗口的设定就变得尤为关键：

1. 归因时间窗口太短，一些样本将被错误的标记成负样本，但未来将完成转化，从而干扰模型学习到了错误标签；

2. 归因时间窗口过长，则，模型无法及时捕获到更新的广告、新发生的用户行为（含转化）等信号，存在模型过时的风险；

相关数据

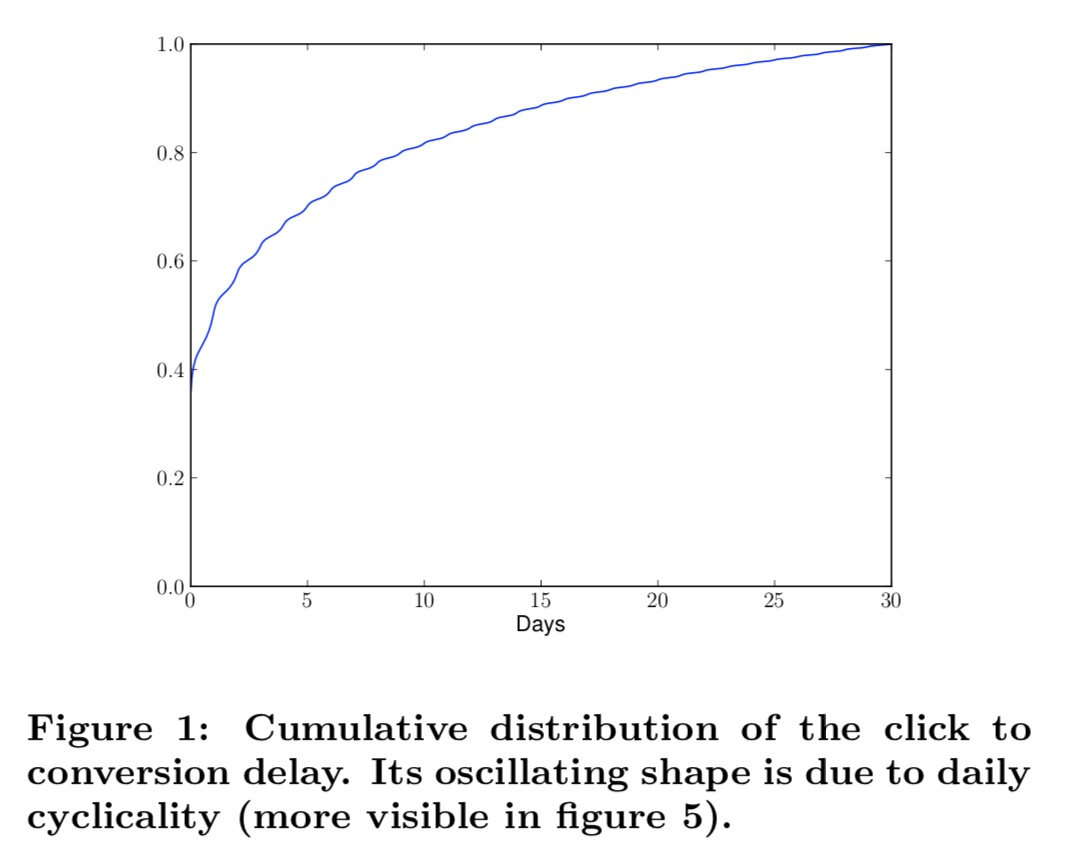
1.转化延迟，

作者提供的数据中2天可以归因约50%左右的订单，相比较曝光-点击延迟，1小时内就可以有95.5%的点击归因。

相比大部分实际业务场景，论文中的转化延迟算是比较长的，例如，很多实际业务场景中t+1天就可以归因90%+的转化，所以cvr模型天级别更新情况下也没有特别大问题。

但论文作者的延迟情况在很多场景中也是存在的，笔者还了解到甚至部分电商场景的延迟比论文中延迟还高（7天归因50%左右订单），所以，在这种场合下，cvr延迟模型的必要性不言而喻。

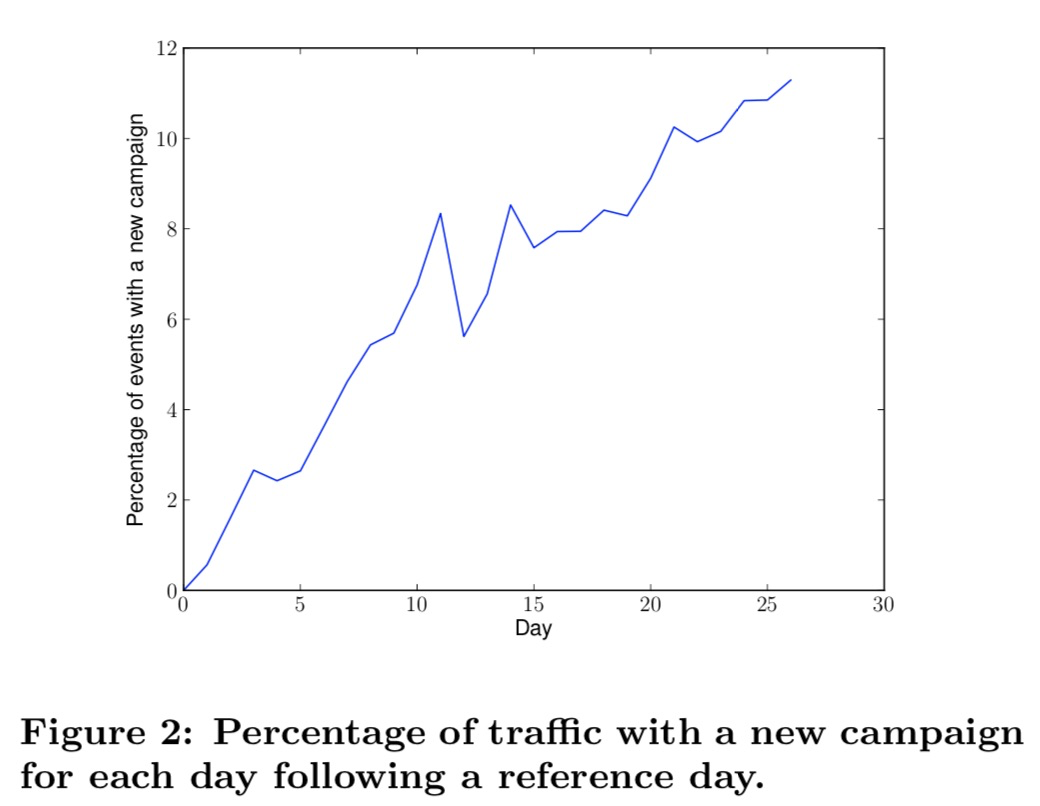
2.广告更新频率

论文对广告的更新频率进行了统计分析，从某一天的广告作为base，统计随着时间增加新增广告的占比。累积26天后，新广告的占比为11.3%。

在实际业务场景下，笔者了解到很多广告的更新频率比论文中的11.3%还高。

这就说明了，归因时间窗口过长，时间窗口的数据无法及时应用到模型中，将会对新广告带来非常大的影响。

解决思路

1.数据方面：

忽略转化归因时间窗口，当点击后已发生转化，标记为正样本，否则被标记为unlabeled（因为，未发生转化的，但将来可能会发生）

2.模型方面：

采用两个模型进行cvr预估：

Conversion Model，用来预估最终是否转化。

Delayed Feedback Model，预估点击后第几天发生转化。

这一模型和生存分析中使用的模型有很大相关性。类似的，对转化问题来说，一些样本是censored（删失的），即在训练时间内无转化，而后续可能有转化。这种情况下，删失样本的转化延迟至少大于从点击开始的流逝时间。

 CVR模型建模

 1.参数说明：

2.场景介绍：

如果用户已经发生转化（Y=1），则C=1恒成立。即，。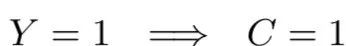

如果用户还未发生转化（Y=0），那么存在两种情况：C=0 或者C=1 & E < D。即，。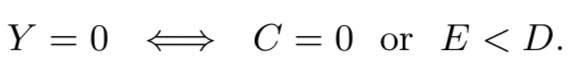

另外，论文还提到一个假设：（C，D）在给定X情况下，与E无关。即

3.训练数据构建：

y=0时，样本集为（x，y，e），

当y=1时，样本集还会增加d，即（x，y，e，d）。

4.CVR建模：

上面已经提到，为了解决下单延迟带来的影响，作者将CVR拆解为两个模型：

（1）conversion model，预测用户最终是否发生转化：采用Logistic Regression进行建模，即。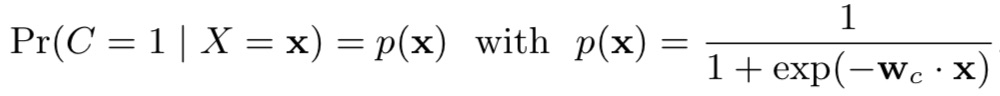

（2）delayed feedback model，预测在d天发生转化的概率：假设转化满足指数分布，即。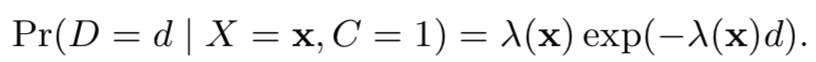

其中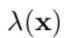，，参考survival analysis学科称为风险函数（hazard function），采用exp(w * x)来建模。

备注：论文中并未对指数分布 & 生存分析（survival analysis）做过多解释，笔者自行查阅和理解，对此部分做简单补充。此部分并非论文内容，感兴趣的同学可以参考文末补充部分。

那么，在d时刻发生conversion的概率估计则为：

在e时刻还未发生conversion的概率估计则为：

其中，

并且，C=0情况下，Y=0也恒成立，即

那么，

5.模型训练

论文采用了两种训练方法：（1）Expectation-Maximization（EM）算法；（2）GD-Joint Learning算法

EM算法：

Expectation step，

求解发生conversion的期望，即，

当Y=1时，C=1恒成立，。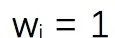

当Y=0时，

Maximization step,

利用wi，求解最大似然（wc、wd）

对上述公式整合，得到最终结果

该公式有两个特点：

（1）p和lamda相互独立，可独立优化，且都是凸函数。

（2）解释性强，p是加权logistic regression，lamda是标准指数回归，wi是对unlabeled数据的缺失数据的表示

GD-Joint Learning算法：

loss function：

其中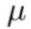，为正则化(L2)系数，其他如下：

采用梯度下降（gradient descent algorithm，L-BFGS）对loss function进行求解。具体求导公式如下（笔者未亲自推导验证）：

在线预估

inference时，只使用conversion model。

delayed feedback model被丢弃。实际业务场景中，该模型，还可以被用来应用于oCPX场景的出价反馈机制中。

以上是论文的主要是思想。实验效果不就再描述。

接下来，下篇文章，我们计划去讲解另外一篇改进文章“A Nonparametric Delayed Feedback Model for Conversion Rate Prediction”。

References

1.Modeling Delayed Feedback in Display Advertising

2.cvr 预估中的转化延迟反馈问题概述：https://zhuanlan.zhihu.com/p/74586059

3.泊松分布&指数分布：https://www.cnblogs.com/think-and-do/p/6483335.html

4.survival analysis：https://www.cnblogs.com/wwxbi/p/6136348.html

附录

指数分布 & 生存分析（survival analysis）相关补充：

1.指数分布：

说指数分布之前，不得不先介绍泊松分布。

泊松分布：是指某段时间内事件发生的概率（例如，某网站平均每分钟有2次访问），即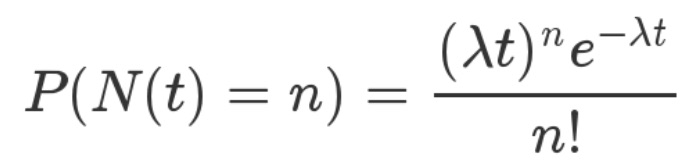，，其中，t表示时间，n表示事件发生的次数，lamda表示事件发生的频率。

指数分布：则是指事件的时间间隔的概率（例如，网站访问的时间间隔）。指数分布的公式可由泊松分布推断出来。如果网站下一次访问的间隔时间 t ，就等同于 t 之内没有访问。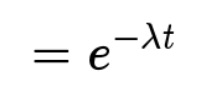

反过来，事件在时间 t 之内发生的概率（至少访问一次的概率），就是1减去上面的值，即

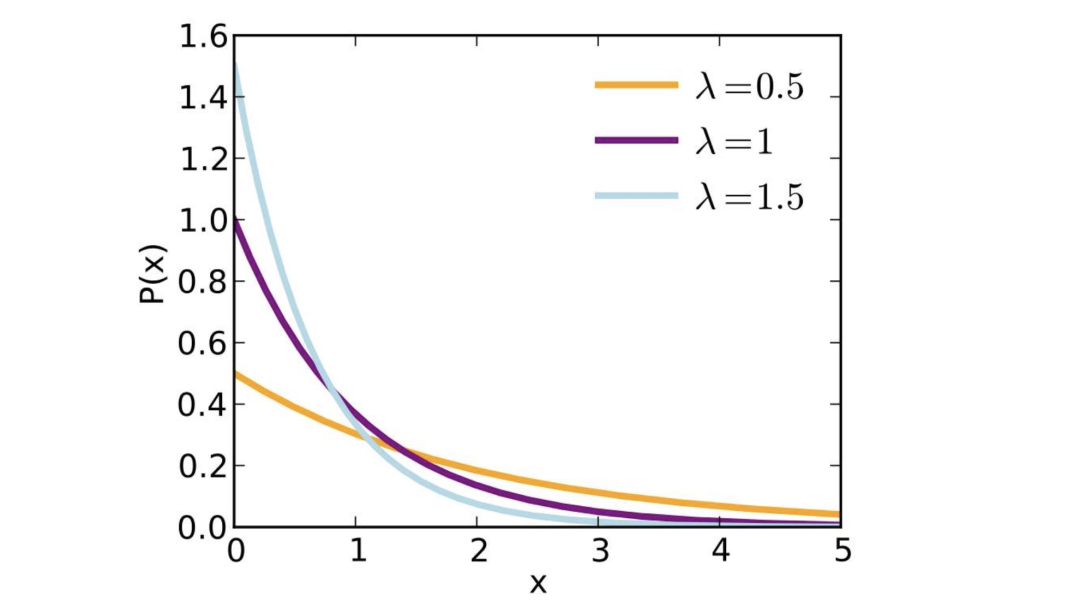
进而，其概率密度函数，曲线如下：

概率密度函数：

对概率密度函数积分，得到指数函数分布：

针对广告cvr场景，则就是，已知C=1情况下：

点击后的d时刻，发生转化的概率，即为

还未发生转化的概率为：p

已发生的概率，p=1-

生存分析（survival annalysis）：

生存分析，对一个或多个非负随机变量进行统计推断，研究生存现象和响应时间数据及其统计规律的一门学科。研究主要对象的寿命超过某一时间的概率，例如，病人感染了病毒后多久会死亡。

常用的几个基本概念：

（1）f(t)：概率密度函数，t时刻死亡概率

，代表截止t时刻的死亡概率

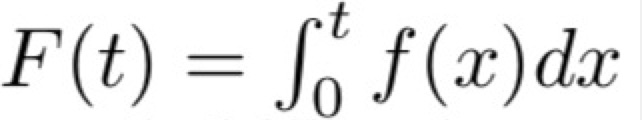
（2）s(t)：生存函数

（3）h(t)：风险函数

CVR的DFM模型假设服从指数分布，其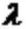在泊松分布中代表的是事件在某段时间发生的频率，此处h(t)风险函数同样可以理解为事件在某时刻下发生的概率，只不过h(t)不是均匀分布，而是符合某种分布。

（4）H(t)：风险累积函数

推荐阅读

AINLP年度阅读收藏清单

当当四折购书，推荐一份书单

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

太赞了！Springer面向公众开放电子书籍，附65本数学、编程、机器学习、深度学习、数据挖掘、数据科学等书籍链接及打包下载

数学之美中盛赞的 Michael Collins 教授，他的NLP课程要不要收藏？

自动作诗机&藏头诗生成器：五言、七言、绝句、律诗全了

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

这门斯坦福大学自然语言处理经典入门课，我放到B站了

征稿启示 | 稿费+GPU算力+星球嘉宾一个都不少

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。