图灵奖Yoshua Bengio ICLR 2020再出新作：通过元学习发掘因果机制

导读

深度学习三巨头图灵奖得主Yoshua Benjio在ICLR 2020上以第一作者身份发表了一篇论文：A Meta-Transfer Objective for Learning to Disentangle Causal Mechanisms，这篇论文被接受为Poster， 提出利用元学习目标，最大限度地提高改变分布的迁移速度，以学习如何模块化获取知识。论文审稿人认为这篇文章包含了新颖有趣的观点，并且解决了审稿人对文章清晰度、参考文献和实验的一些其他问题。因此，它对ICLR做出了有价值的贡献。

论文地址：

https://static.aminer.cn/misc/pdf/untitled.pdf

论文评点：

本文提出通过元学习来发现因果机制，并提出了一种方法。审稿人对关键假设(正确的因果模型意味着更高的预期在线可能性)没有得到理论或实际数据实验的充分支持表示担忧。作者指出，最近的一篇论文建立在这项工作的基础上，并对更现实的问题设置进行了测试。尽管如此，最新的论文并没有衡量在线适应的可能性，只是衡量适应过程中的训练错误，这表明本文的方法可能更糟。尽管存在这些问题，但审稿人普遍认为这篇文章包含了新颖有趣的观点，并且解决了审稿人对文章清晰度、参考文献和实验的一些其他问题。因此，它对ICLR做出了有价值的贡献。

摘要

我们提出利用元学习目标，最大限度地提高改变分布的迁移速度，以学习如何模块化获取知识。特别是，我们关注如何在与因果关系一致的情况下将联合分布纳入适当的条件。我们解释如果这可行，假设分布的变化是局部化的（distributions are localized）(例如由于对其中一个变量的干预而导致其中一个边缘marginal)。我们证明，在这种假定的因果机制的局部变化的情况下，正确的因果图将趋向于仅有几个具有非零梯度的参数，即需要调整的参数(修改变量的参数)。实验观察到这会导致自适应更快，并利用这一性质来定义一个元学习替代评分，它除了连续的图参数化外，还将有利于正确的因果图。最后，我们考虑到AI智能体方面（例如，机器人自主发现其环境），我们考虑了相同的目标如何能够发现因果变量本身，因为观察到的低水平变量没有因果意义。双变量实例中的实验验证了所提出的思想和理论结果。

引言

用于训练我们的模型的数据通常被假定为独立同分布的(iid.)。同样，模型的性能通常使用来自同一分布的测试样本来评估，假设它们代表了所学习的系统的使用情况。虽然从统计的角度对这些假设进行了很好的分析，但在许多实际应用中它们很少能得到满足。例如，根据一家医院的历史数据进行训练的医疗诊断系统对来自另一家医院的病人可能表现不佳，原因是分布情况发生了变化。理想情况下，我们希望我们的模型能够很好地生成（generalize），并且能够快速地适应分布外的数据。

然而，为了成功地转移到一种新的分布上，人们可能需要更多关于手头数据的信息。在本文中，我们不考虑对数据分布的假设，而是考虑它如何改变（例如，从训练分布到转移分布时，可能导致某些Agent的动作）。我们关注的假设是，当知识以适当模块化的方式来表示时，只有一个或几个模块发生改变，这些变化是稀疏的。当分布变化是由于一个或多个Agent的行动所致时，这一点尤其重要，因为Agent在特定的地点和时间进行干预，这体现在因果关系文献中讨论的干预措施的形式上，即其中一个因果变量被限制在一个特定值或一个随机变量上。一般来说，Agent一次很难影响许多潜在的因果变量，虽然本文并不是关于Agent学习本身，但这是我们探索的一个性质，以帮助发现这些变量以及它们之间的因果关系。在这种情况下，因果图（casual graph）是一个强大的工具，因为它告诉我们干预变量分布中的扰动将如何传播到所有其他变量并影响它们的分布。

本文贡献

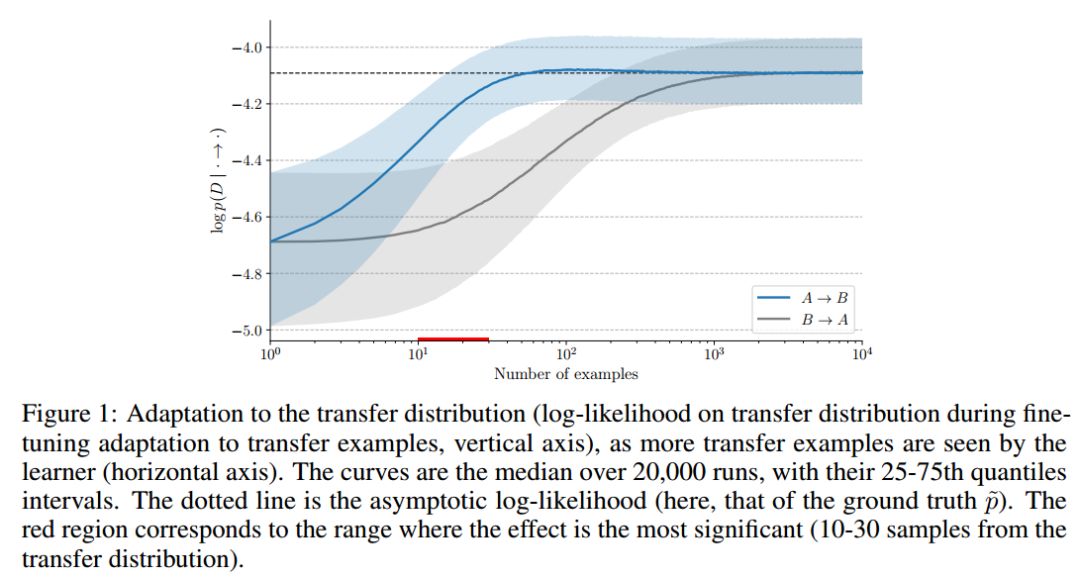
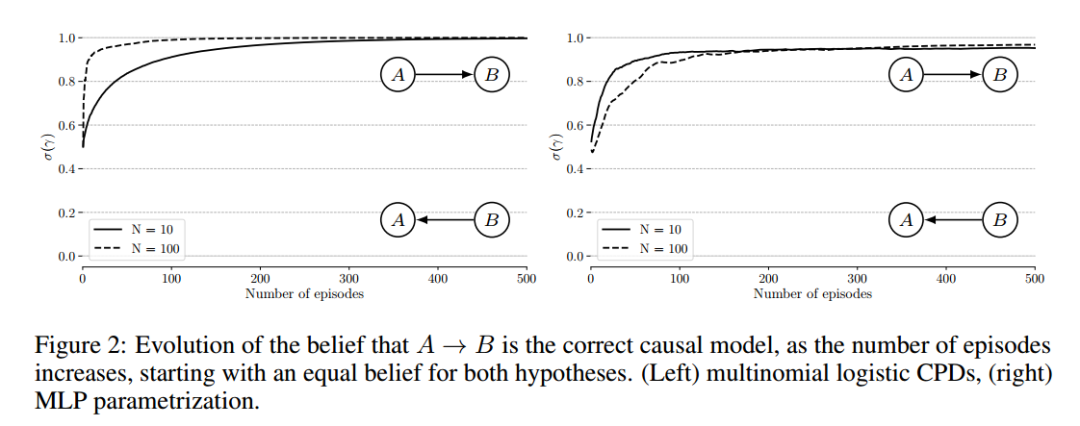
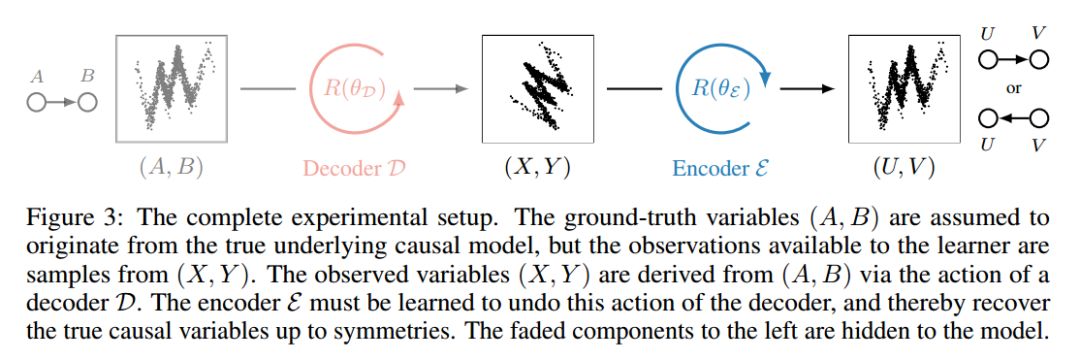
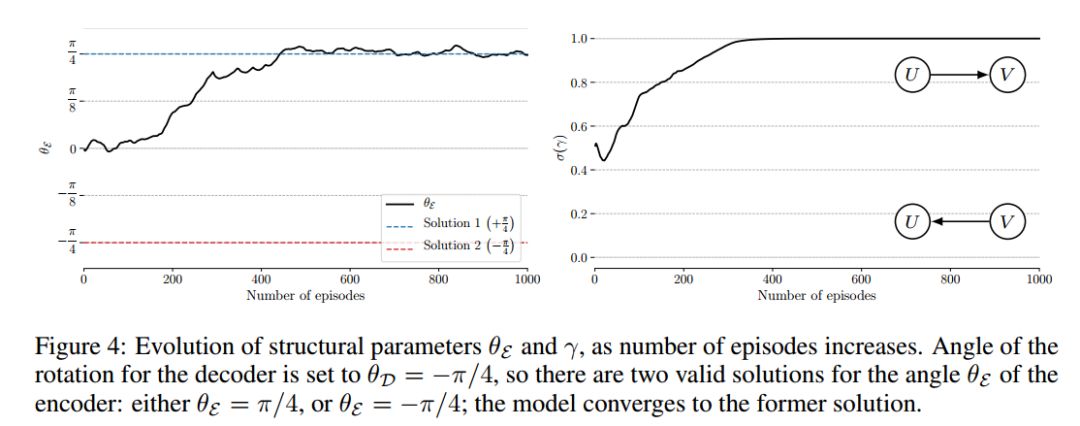
我们首先对合成数据进行验证，即当在对真实的双变量因果图(learner不知道)进行一定的干预后，当提供样本数据时，正确地捕捉底层因果结构的模型适应速度更快。这表明，适应速度确实可以作为分数来评估learner是否适合潜在的因果图。然后，我们使用因果图的平滑参数以一种端到端的方式直接优化这个分数。最后，我们在一个简单的设置中表明，在未知的混合变量的情况下，可以利用分数来区分正确的因果变量。

讨论与未来工作

虽然本文的重点是因果图，但提出的目标是由一个更普遍的问题所驱动的，即发现潜在的因果变量及其依赖关系，以解释学习者的环境，并使学习者有可能在由于自我或他人的干预而产生的变化下做出适当的计划。底层解释性变量的发现有不同的名称，尤其是底层变量分离的概念(Bengio et al.， 2013;Locatello et al，2019年)，并在因果设定研究(Chalupka et，2015);和领域适应(Magliacane et al.， 2018)。本文也与元学习相关(Finn et al.，2017; Finn, 2018; Alet et al.， 2018; Dasgupta et al.， 2019)，到贝叶斯结构学习(Koller & Friedman, 2009;Heckerman et al，1995; Daly et al，2011;chicken, 2002b)，因果发现(Pearl, 1995; Tian & Pearl, 2001; Pearl, 2009; Bareinboim & Pearl, 2016; Peters et al., 2017);以及非平稳性如何使因果发现更容易(Zhang et al.， 2017)。有关工作的详细讨论见附录A。

我们已经确定，在非常简单的双变量设置中，学习者适应观测数据分布的稀疏变化的速度可以用来推断因果结构，并解开因果变量。这依赖于一个假设，即有了正确的因果结构，这些分布上的变化是局部的。我们通过理论结果和实验验证来证明这些观点。这里提供了实验的源代码。

https://github.com/ec6dde01667145e58de60f864e05a4/CausalOptimizationAnon

这项工作只是基于对修正分布适应速度的因果结构学习方向上的第一步。在实验方面，除了这些研究之外，还需要考虑许多其他设置，包括不同种类的参数化、更丰富和更大的因果图(参见Ke等人(2019)基于本文的第一个版本)，或不同种类的优化过程。此外，还需要做更多的工作，以探索如何使用提出的想法，以学习良好的表示，其中的因果变量是解开。将这些思想整理出来，就可以应用于改进学习代理处理非平稳的方法，从而提高这些代理的样本复杂度和健壮性。

一种关于解缠的极端观点是，解释变量应该是略微独立的，并且许多深层生成模型(Goodfellow et al.， 2016)和独立成分分析模型(Hyvarinen et al.， 2001;(Hyvarinen et al.， 2018)建立在这个假设之上。然而，我们用自然语言操作的高级变量并不是完全独立的:它们通过通常用句子表达的语句(例如，一个经典的象征性人工智能事实或规则)相互关联，一次只涉及几个概念。这种假设被提出是为了帮助从原始的观察中发现相关的高层次表征，如先验意识(Bengio, 2017)，其观点是人类在任何特定时间都只关注我们意识中出现的少数概念。在这里提出的工作可以提供一个有趣的元学习方法，以帮助学习这样的编码器输出的因果变量，以及找出如何得出的变量之间的相互关系。在这种情况下，我们应该区分两个重要的假设: 第一个是因果图是稀疏的，这是结构学习中的一个常见假设(Schmidt et al.， 2007);二是分布的变化是稀疏的，这是本文的重点。

（本文转载自“专知”微信公众号，感谢原作者的精彩分享。如需转载请联系原作者。）

往期精彩回顾

【NeurIPS100】NeurIPS2019 七篇获奖论文揭晓 入选论文深度分析！

NeurIPS十年高引学者TOP100榜单发布！这些大牛值得膜拜！

【NeuIPS 2019】Yoshua Bengio报告：如何用深度学习来实现System2？

点击“阅读原文”查看更多精彩↓