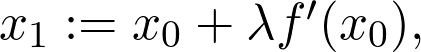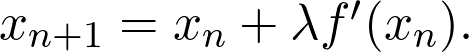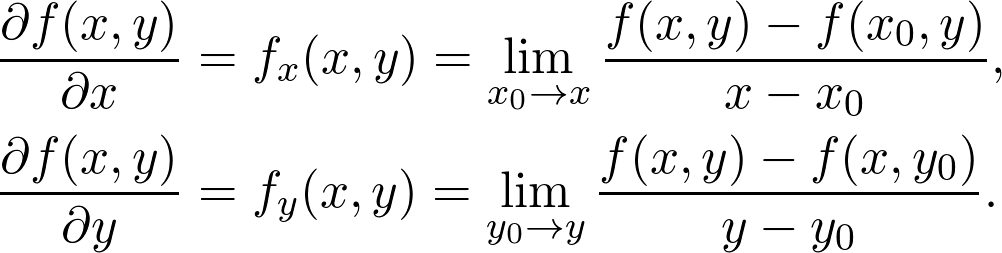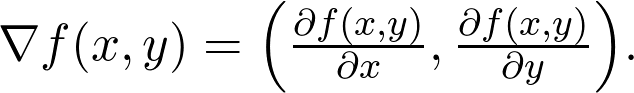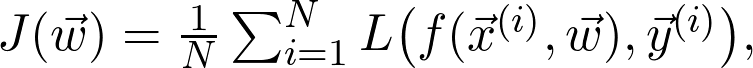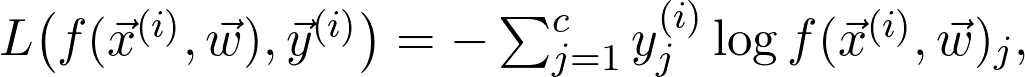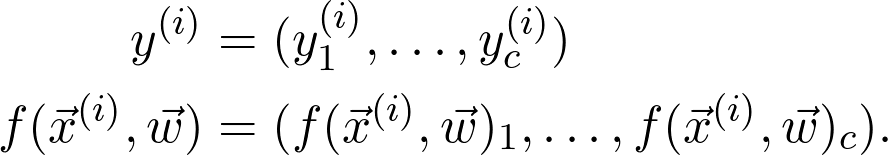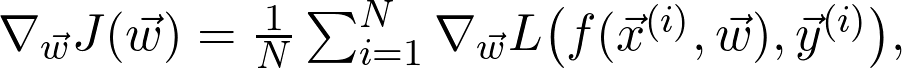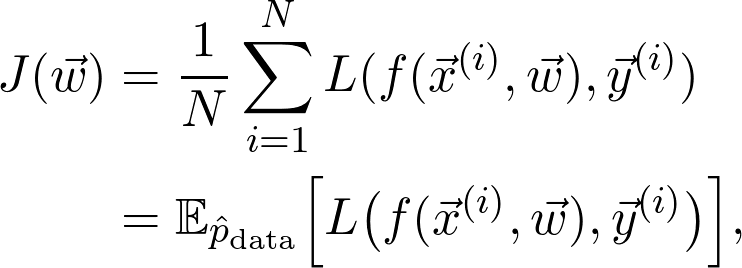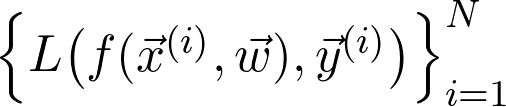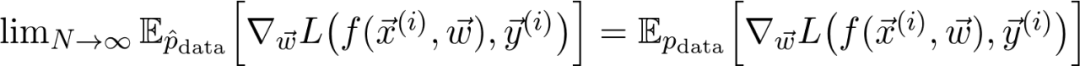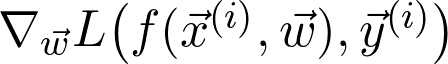【基础】优化背后的数学基础
点击上方,选择星标或置顶,每天给你送干货
阅读大概需要14分钟
跟随小博主,每天进步一丢丢
转载自:机器之心
参与:李诗萌、张倩
作者:Tivadar Danka
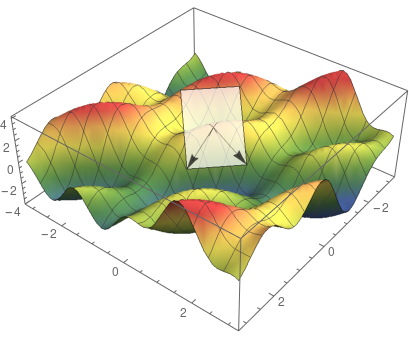
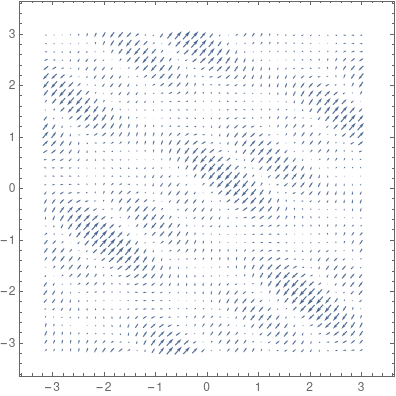
深度学习中的优化是一项极度复杂的任务,本文是一份基础指南,旨在从数学的角度深入解读优化器。
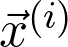 是观测值为
是观测值为
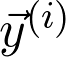 的第 i 个数据点
的第 i 个数据点
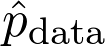 是训练数据给出的(经验)概率分布。
可以将序列写成:
是训练数据给出的(经验)概率分布。
可以将序列写成:
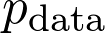 是真正的总体分布(这是未知的)。
再详细点说,因为增加了训练数据,损失函数收敛到真实损失。
因此,如果对数据二次采样,并计算梯度:
是真正的总体分布(这是未知的)。
再详细点说,因为增加了训练数据,损失函数收敛到真实损失。
因此,如果对数据二次采样,并计算梯度:


登录查看更多
相关内容
Arxiv
9+阅读 · 2019年10月12日