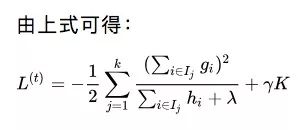计算：XGBoost背后的数学之美

来源：KDnuggets

编译：Bot

编者按：说到Kaggle神器，不少人会想到XGBoost。一周前，我们曾在“从Kaggle历史数据看机器学习竞赛趋势”介绍过它的“霸主地位”：自提出后，这种算法在机器学习竞赛中被迅速普及，并被多数夺冠模型视为训练速度、最终性能提升的利器。那么，你知道XGBoost背后的数学原理是什么吗？

好奇的李雷和韩梅梅

李雷和韩梅梅是形影不离的好朋友，一天，他们一起去山里摘苹果。按照计划，他们打算去摘山谷底部的那棵大苹果树。虽然韩梅梅聪明而富有冒险精神，而李雷有些谨慎和迟钝，但他们中会爬树的只有李雷。那么他们的路径是什么呢？

如上图所示，李雷和韩梅梅所在的位置是a点，他们的目标苹果树位于g点。山里环境复杂，要怎么做才能确定自己到了山谷底部呢？他们有两种方法。

1.由韩梅梅计算“a”点的斜率，如果斜率为正，则继续朝这个方向前进；如果为负，朝反方向前进。

斜率给出了前进的方向，但没有说明他们需要朝这个方向移动多少。为此，韩梅梅决定走几步台阶，算一下斜率，确保自己不会到达错误位置，最终错过大苹果树。但是这种方法有风险，控制台阶多少的是学习率，这是个需要人为把控的值：如果学习率过大，李雷和韩梅梅很可能会在g点两侧来回奔走；如果学习率过小，可能天黑了他们都未必摘得到苹果。

听到可能会走错路，李雷不乐意了，他不想绕远路，也不愿意错过回家吃饭的时间。看到好友这么为难，韩梅梅提出了第二种方法。

2.在第一种方法的基础上，每走过特定数量的台阶，都由韩梅梅去计算每一个台阶的损失函数值，并从中找出局部最小值，以免错过全局最小值。每次韩梅梅找到局部最小值，她就发个信号，这样李雷就永远不会走错路了。但这种方法对女孩子不公平，可怜的韩梅梅需要探索她附近的所有点并计算所有这些点的函数值。

XGBoost的优点在于它能同时解决以上两种方案的缺陷。

梯度提升（Gradient Boosting）

很多梯度提升实现都会采用方法1来计算目标函数的最小值。在每次迭代中，我们利用损失函数的梯度训练基学习器，然后用预测结果乘上一个常数，将其与前一次迭代的值相加，更新模型。

它背后的思路就是在损失函数上执行梯度下降，然后用基学习器对其进行拟合。当梯度为负时，我们称它为伪残差，因为它们依然能间接帮助我们最小化目标函数。

XGBoost

XGBoost是陈天奇在华盛顿大学求学期间提出的成果。它是一个整体加法模型，由几个基学习器共同构成。

那么，我们该如何在每次迭代中选择一个函数？这里可以用一种最小化整体损失的方法。

在上述梯度提升算法中，我们通过将基学习器拟合到相对于先前迭代值的损失函数的负梯度，在每次迭代时获得f_t(x_i)。而在XGBoost中，我们只探索几个基学习器或函数，选择其中一个计算最小值，也就是韩梅梅的方法2。

如前所述，这种方法有两个问题：

1. 探索不同的基学习器；

2. 计算所有基学习器的损失函数值。

XGBoost在计算基学习器f_t(x_i)最小值的，使用的方法是泰勒级数逼近。比起计算精确值，计算近似值可以大大减轻韩梅梅的工作量。

虽然上面只展开到二阶导数，但这种近似程度就足够了。对于任意f_t(x_i)，第一项C都是常数。g_i是前一次迭代中损失的一阶导数，h_i是其二阶导数。韩梅梅可以在探索其他基学习器前直接计算g_i和h_i，这就成了一个简单的乘法问题，计算负担大大减轻了，不是吗？

解决了损失函数值的问题，我们还要探索不同的基学习器。

假设韩梅梅更新了一个具有K个叶子节点的基学习器f_t。设I_j是属于节点j的实例集合，w_j是该节点的预测。因此，对于I_j中的实例i，我们有f_t(x_i)=w_j。所以我们在上式中用代入法更新了L^(t)的表达式。更新后，我们就能针对每个叶子节点的权重采用损失函数的导数，以获得最优权重。

以上就是对于具有K个叶子节点的基学习器的最佳损失。考虑到这样的节点会有上百个，一个个探索它们是不现实的。

所以让我们来看韩梅梅的情况。她现在已经知道如何使用泰勒展开来降低损失计算量，也知道了什么是叶子节点中的最佳权重。唯一值得关注的是如何探索所有不同的树结构。

XGBoost不会探索所有可能的树结构，它只是贪婪地构建一棵树，选择导致最大损失的方法，减少分叉。在上图中，树从节点I开始，根据标准，节点分为左右分叉。所以我们的实例一部分被放进了左侧的叶子节点，剩下的则去了右侧的叶子节点。现在，我们就可以计算损失值并选择导致损失减少最大的分叉。

解决了上述问题后，现在韩梅梅就只剩下一个问题：如何选择分叉标准？XGBoost使用不同的技巧来提出不同的分割点，比如直方图。对于这部分，建议去看论文，本文不再作解释。

XGBoost要点

1. 虽然梯度提升遵循负梯度来优化损失函数，但XGBoost计算每个基学习器损失函数值用的是泰勒展开。

2. XGBoost不会探索所有可能的树结构，而是贪婪地构建一棵树。

3. XGBoost的正则项会惩罚具有多个叶子节点的树结构。

4. 关于选择分叉标准，强烈建议阅读论文：arxiv.org/pdf/1603.02754.pdf

原文地址：www.kdnuggets.com/2018/08/unveiling-mathematics-behind-xgboost.html