KDD'22 | GraphWorld 图的世界是啥样的？

2022 年 9 月 6 日 图与推荐

论文地址：https://arxiv.org/pdf/2203.00112.pdf
论文代码：https://github.com/google-research/graphworld
欢迎关注小编知乎：戴鸽

谷歌大佬新的图网络Benchmark。与以往堆数据的benchmark不同，这篇文章指出了单纯堆数据量可能并不让图模型学到有用的信息，与其是简单的数据量，对图模型更重要的应该还是图结构本身的数据是什么样子的。

Introduction

目前来说，在图网络领域有大量的benchmark的数据集，然后大家可以在这些数据上测试新的图网络算法。但是由于数据本身可能有一些特性，导致一般情况下不能说一个新模型能通用到所有数据上，甚至一个新的模型可能会针对一个特殊的数据集产生结构上的过拟合（architectural overfitting），并且，作者认为目前的一些工作可能只是模型参数量的增加，并没有理解图本身的信息，因此很难说模型变好到底是参数量增加了还是模型真的学到了数据性质。

基于以上想法，作者提出了GraphWorld这种合成的通用Benchmark来衡量模型在图网络上的效果。首先做一个简单测试，作者设了一些合成数据，并且把现在已有的数据集也映射到了这些合成数据集的分布里面。x和y轴分别表示图数据的同质性和出入度，z表示一些经典模型与其他baseline模型预测精度对比（MRR指标， mean reciprocal rank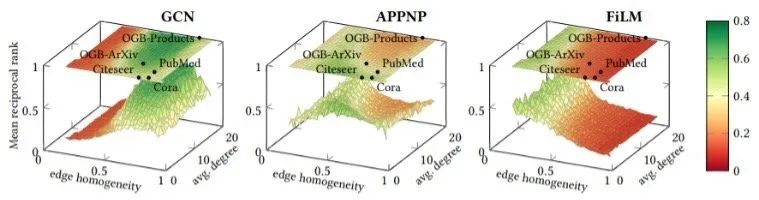）从这个简单实验上可以看出来，GNN模型在不同数据集上实际上是有明显差异的，尤其是在不同的虚拟数据集上。由于这些都是虚拟数据，所以现在数据已经在TF-GNN上更新开源了。由此可见，仅仅依靠现在广泛使用的图网络benchmark是有局限性的。

图网络数据集的缺陷

首先，图数据的benchmark大多分布相似，因此，训练出来的图网络大概率是只能针对某种数据的网络。而现实中的图网络又不一定符合benchmark里面的样子，所以直接导致在benchmark里能顺利训练出来的图结构不一定能符合真实场景。这里做了一个简单统计：

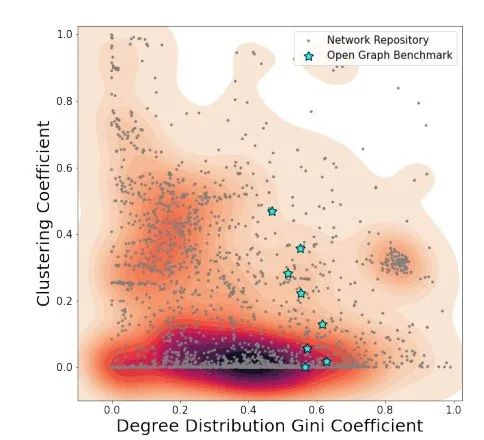
现在的benchmark的数据只是图网络世界中的一部分。虽然这里说的图网络数据大多没有标签，但还是反应了一个真实的数据分布情况，因此有理由相信如果这些数据有标签了，现在的图神经网络可能就不一定有用了。

其次，增量的网络结构有可能导致结构上的过拟合，在NLP[1]和CV[2]领域已经有过相似结论了，因此在图上也是有可能的。

最后，虽然我们可以增加图数据的大小，但这个成本很大，也不太可能能够迅速调整出真正能适用于多种图网络分布下的图网络结构。

GraphWorld

设是图的集合，为特征，如果是节点分类任务，可以设为标签，图的测试集合可以表示为。同时为了方便用户使用GraphWorld，作者设置了一系列参数并且使用用采样函数来生成用户需要的图数据，得到，在此基础上，在对模型进行划分，得到。另一方面，如果图被采样的过小，图模型的效果是不一定准确的。比如如果采样数据很小，GNN模型将很难从边连接的角度学到东西，导致的结果是要么过拟合，要么学不会。因此在采样上，图应该足够大。

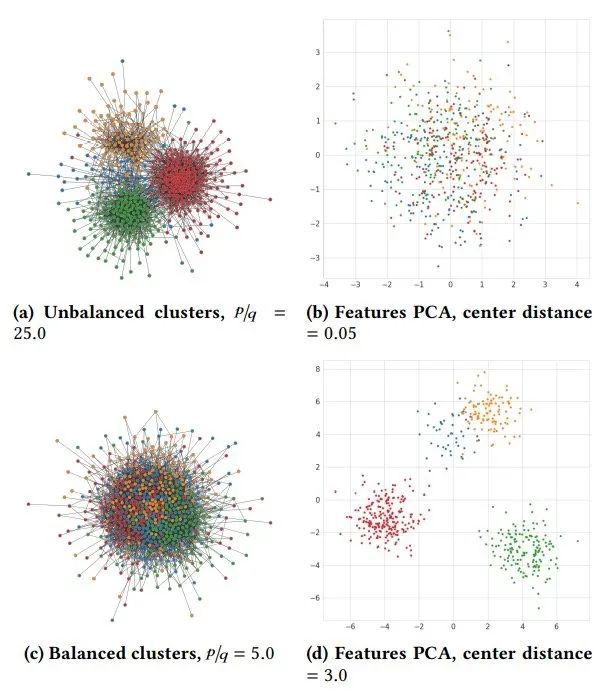
举例来说，对图样本的采样可以根据节点特征是否为一个聚类集合来划分，即p-to-q ratio。这里p和q分别表示边连接的两个节点是否被聚类成同一类别。如图所示可以直观的看出根据p-to-q ratio 划分出来的图结构：

实验

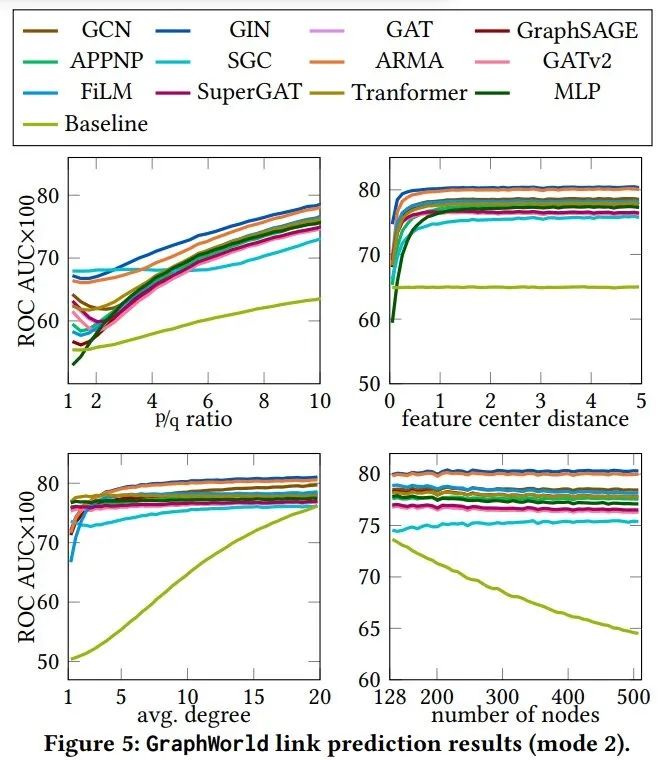
实验部分作者用从数据库中采样得到的图数据做了一些分析。首先是对节点分类得到的实验结果，作者采用了多种图模型进行测试，其中baseline模型应该是指的逻辑回归。可以发现，如果单纯的增加节点数量，实际上是不会对模型准确率产生影响的。真正对大多数模型性能产生重要影响的还是p/q ratio和特征。另外，基于注意力机制的GAT系列模型也没有表现的特别好，甚至在按照特征中心距离划分的数据集上表现不佳；但如果仅仅依靠特征，如MLP模型，也不会在p/q ratio的数据上表现良好。同时，在边预测任务上也能发现相同的结果：然而在边预测的任务上模型的差异性并没有像节点分类数据这样明显。另外，图分类任务也可以做：这里的mode 1，2，3是3种参数选择方法，比如固定参数，多轮最优，还有作者提出的适用于GraphWorld的调参方法。这个实验也能发现也就GIN的mse能在1以下了，其原因可能是GIN确实能学到一些结构信息，而其他模型甚至不能达到1以下的mse，甚至不如逻辑回归。。。这里的逻辑回归采用的特征也就是边密度。。。这与另一篇NeuIPS文章得到了相似的结论[3]。

参考文献

[1] Yixin Nie, Adina Williams, Emily Dinan, Mohit Bansal, Jason Weston, and Douwe Kiela. 2019. Adversarial NLI: A new benchmark for natural language understanding. arXiv preprint arXiv:1910.14599 (2019)

[2] Benjamin Recht, Rebecca Roelofs, Ludwig Schmidt, and Vaishaal Shankar. 2018. Do cifar-10 classifiers generalize to cifar-10? arXiv preprint arXiv:1806.00451 (2018).

[3] Zhengdao Chen, Lei Chen, Soledad Villar, and Joan Bruna. 2020. Can graph neural networks count substructures? arXiv preprint arXiv:2002.04025 (2020).