作者:北邮GAMMA Lab硕士生 于越 本文旨在简要总结近期的图对抗攻击中的黑盒攻击方法,带领读者了解图黑盒攻击的基本定义和最新进展。
1 简介
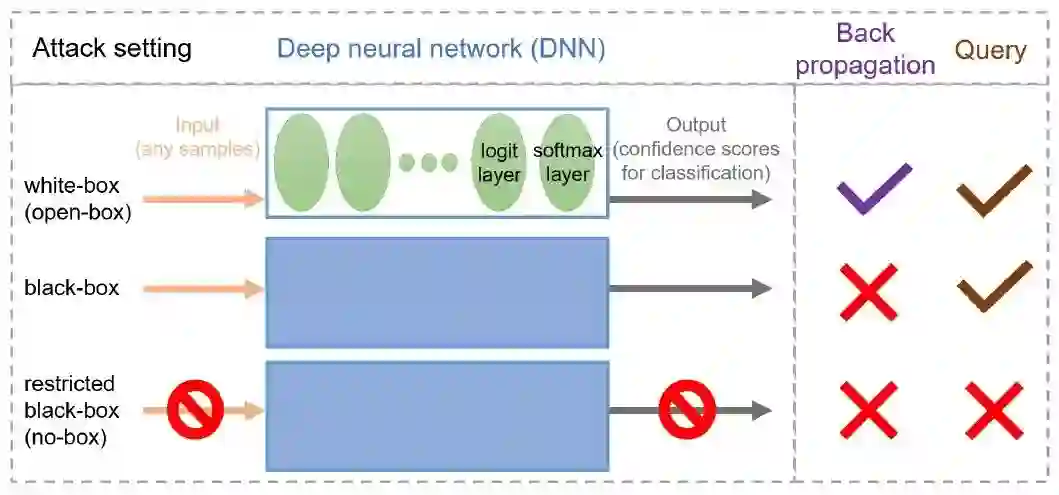
图神经网络(GNN)广泛应用于图数据挖掘,例如社交网络、电商数据、金融数据等等。常见的图神经网络有GCN、GAT、APPNP等。然而,现有的GNN易受到对抗攻击的影响,导致性能的大幅下降。对抗攻击是指攻击者通过修改少量数据的方式使神经网络性能明显下降。而人类通常不会被这类扰动所影响,因为人类的判断是比较鲁棒的。因此,对抗攻击及防御是如今可信AI的研究热门。图对抗攻击中,攻击者通过修改节点属性或拓扑结构来使图模型的性能下降。d对于最常见的拓扑攻击,形式化表述为其中为攻击损失函数,是参数为的GNN,为图的邻接矩阵,为扰动后的邻接矩阵,为特征矩阵,为扰动代价(budget),含义是扰动边数量的最大值。图攻击也可以看作一种基于目标函数的优化过程。对抗攻击有多种设定,如下图所示。白盒攻击中,攻击者可以获取输入数据,模型预测(最终预测的置信度向量)和模型的结构信息,并且可以获取反向传播的梯度信息;黑盒攻击中,攻击者只能获取输入数据和预测结果,根据预测结果是置信度还是one-hot向量又分为软标签和硬标签攻击。图黑盒攻击中,攻击者可以获取以及预测矩阵。黑盒攻击由于其设定更接近实际场景,因此近期受到的关注逐渐增多。
2 方法介绍
2.1 Towards More Practical Adversarial Attacks on Graph Neural Networks (NeurIPS 2020)
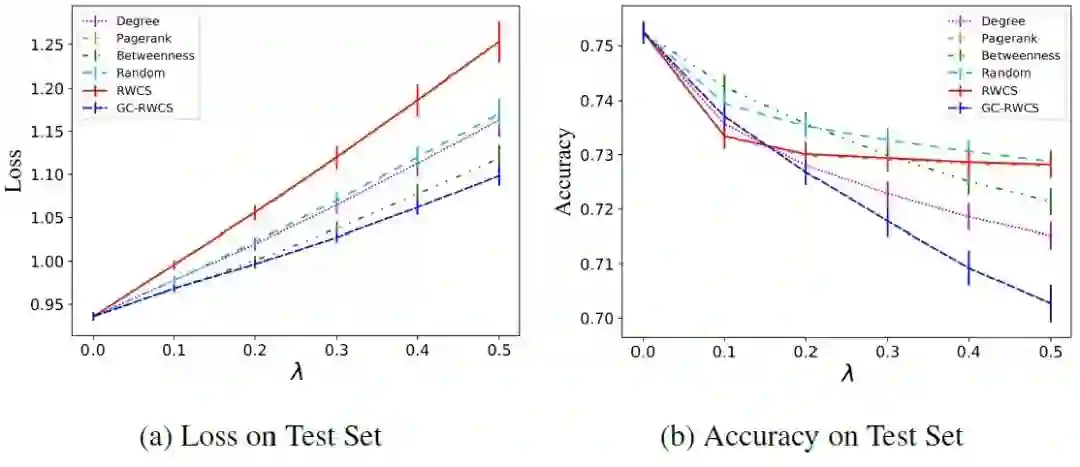
原文:https://arxiv.org/abs/2006.05057本文在黑盒的基础上采取了更加现实的设定:攻击节点的度和数量都有所限制(对于社交网络,不能攻击名人节点),而且无法获取模型预测。本文主要关注攻击节点的选取。白盒攻击常采取的目标函数Carlini-Wagner Loss为其中为最后一层节点表示,即预测矩阵。该损失函数含义为,每个节点预测的最大置信度与真实标签对应的置信度之差的和。损失函数越大,说明模型的预测中,错误结果与真实结果相去甚远,因此攻击效果越好。作者证明了使用该损失函数时,某个节点的扰动带来的损失函数变化的一阶近似期望与图随机游走矩阵该列之和相关。因此,可以选取随机游走矩阵列求和最大的几个节点进行攻击,即RWCS方法。实验结果表明,随着扰动强度的增加,损失函数线性增大,但是分类正确率在扰动强度达到一定值之后不再减小。这说明Loss和ACC之间存在不匹配的关系。这种不匹配关系暗示了攻击的冗余特性。
因此,本文提出了修正的方法GC-RWCS:
其中为二值化的随机游走矩阵为评分函数,,对的列求和。这个算法做了如下几个改进:第6行每次迭代去掉选中节点跳邻居,因为攻击具有同配性(邻居节点对攻击的贡献与节点本身类似);第7至10行,更新某些特定行的值,因为代表攻击很可能会让分类错误,因此更新矩阵第行为0,让不再对攻击节点选取有贡献。
2.2 A Hard Label Black-box Adversarial Attack Against Graph Neural Networks (CCS 2021)
原文:http://arxiv.org/abs/2108.09513
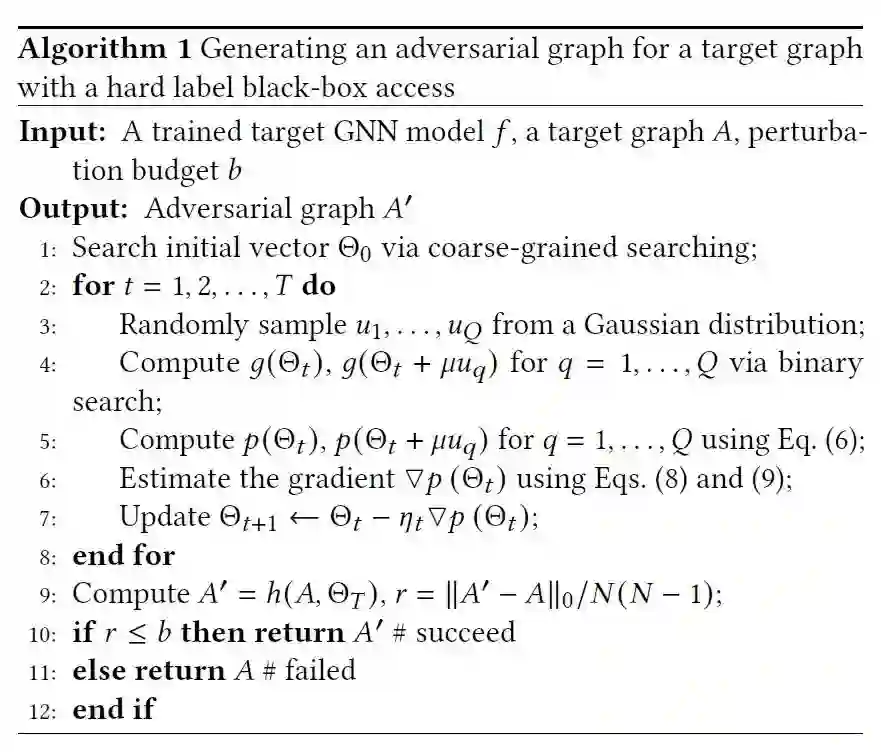
本文是硬标签的设定,即攻击者只知道模型预测的one-hot结果而非置信度。并且,作者发现图攻击的复杂度会随着节点数量的增加而指数级增加,因此首先将邻接矩阵连续化(这也是很多基于优化的图攻击的做法)。其中为扰动函数,为扰动矩阵。由于本文是图分类攻击模型,因此优化问题可以表示为定义图结构沿着扰动到分类边界的距离为,因此我们需要的最小的扰动的个数为。我们的目标就是选取让最小的,为了优化,实际中使用1范数替代0范数。算法如下
其中梯度的估计方式如下同时,本文提出了粗粒度到细粒度的扰动搜索策略,将图根据聚类结果抽象为超点和超边,按照超点-超边-全图的顺序搜索扰动,能够提高效率。
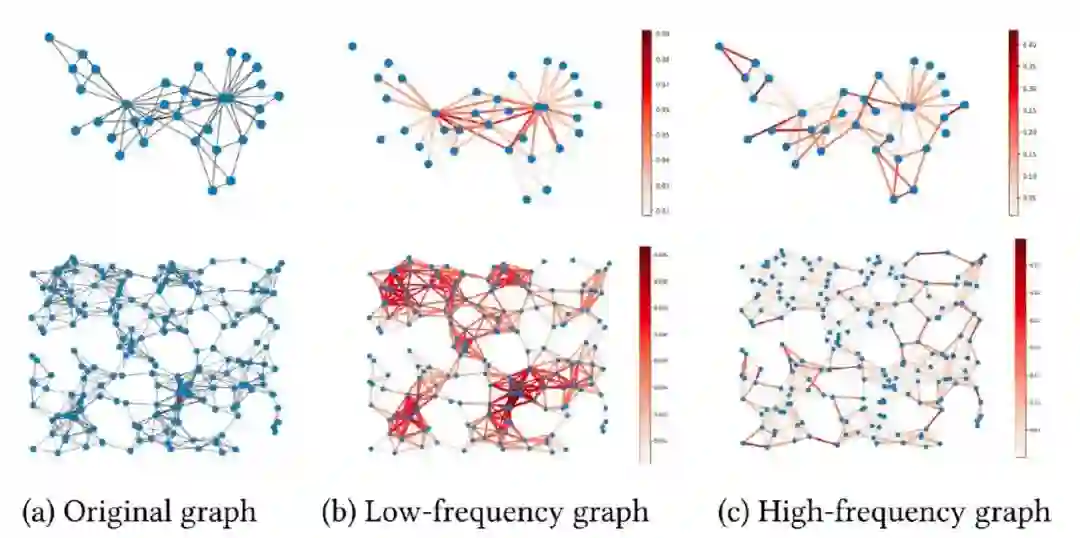
2.3 Graph Structural Attack by Perturbing Spectral Distance (KDD 2022)
因此,作者认为在谱域对图进行攻击是更有效率的。具体算法如下
作者认为,频谱的距离,即特征值之差的2范数代表了攻击的效果,因此Loss如第8行所示。为了减少特征值分解的开销,每m步中,有m-1步使用近似算法,即第10行。
3 总结
黑盒攻击具体的定义并不完全明确,而且具体问题的设置又有一些细微差别。因此,研究黑盒攻击首先需要定义问题。根据问题定义,就会导出这个设置下解决问题的关键。黑盒攻击无法获取模型梯度,因此定义损失函数和梯度估计方法是两个比较重要、需要考虑的点。 本期责任编辑:杨成本期编辑:刘佳玮