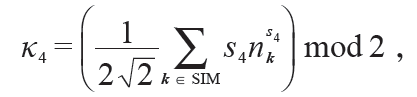基于对称性指标预测拓扑材料(下)
作者:唐峰1,2 万贤纲1,2
(1 南京大学物理学院固体微结构物理国家重点实验室)
(2 南京大学人工微结构科学与技术协同创新中心)

摘要 拓扑材料是凝聚态物理和材料科学领域的前沿课题。随着理论方法的发展,最近人们在大规模筛选拓扑材料方向取得了多个进展。文章着重介绍作者基于对称性指标理论发展的根据在原子绝缘体基组展开系数高效判断材料拓扑性质的方法,以及相关的典型材料。人们预言的数千个新的拓扑体系为进一步深入研究拓扑材料提供了基础。
关键词 拓扑量子体系,空间群及能带不可约表示,对称性指标理论,原子绝缘体基组,拓扑材料判定新方法


众所周知,一个有中心反演对称性的材料,其原子绝缘体在演化的过程中如果其价带和导带的宇称在奇数个时间反演不变点处发生了翻转,该材料变成强拓扑绝缘体[84],可对应于Z4 SI 群中1 和3 的情况。当发生能带翻转的是2 或者6 个时间反演不变点时,根据Fu—Kane判据可知体系不是拓扑绝缘体,但是后续的研究表明,这时候该体系将会属于Z4 SI 群中2 的情况,不能绝热地变到原子绝缘体,可能是高阶拓扑晶体绝缘体或者是镜面陈绝缘体[92,93]。目前已知的高阶拓扑晶体绝缘体数目还非常有限,所以基于上述拓扑材料搜索方案我们首先在无机材料数据库(ICSD)[94]中搜索了第2,11,12,61,136,166 和227 号空间群的所有材料。这7 个空间群均具有Z4 SI 群,我们找到了多个高阶拓扑绝缘体体系[88]。也在ICSD数据库里搜索了具有高阶SI 群(Z8和Z12)的体系[91],这类体系具有丰富的晶格对称,我们发现了许多属于这类体系的拓扑材料,并对其中石墨(SG194)和Pt3Ge (SG140)材料做了具体的拓扑性质分析[91]。
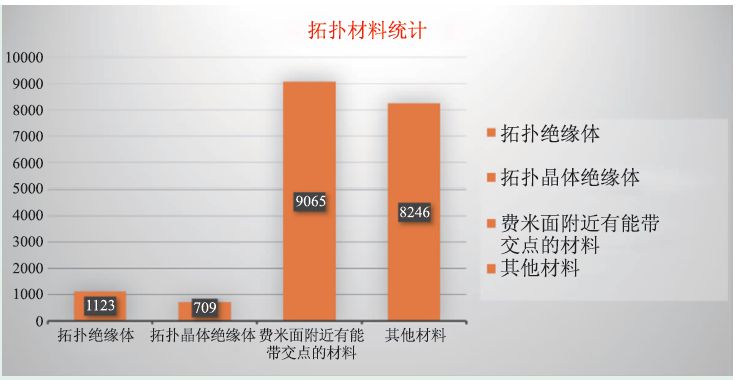
这一方法非常高效,因此我们也用其对ICSD晶体库[94]中所有的材料进行了拓扑性质的判断和筛选[90,91]。ICSD晶体库搜集了人们已经成功生长出来的大约有18 万个晶体材料,然而其中大量的材料原子占据不是整数,基于密度泛函理论的第一性原理计算方法处理这些体系有一定困难,所以在研究中排除掉了这些体系。LDA和GGA势函数在处理电子关联强的体系有很大的局限性,我们也排除掉了含有3d、4f 以及部分4d/5d 元素(Tc,Ru,Rh,Os,Ir)的材料体系。5f 锕系核材料体系不利于实际应用,也被排除掉了。最终通过上述初筛,得到19143 个晶体材料,然后基于我们的拓扑材料搜索算法,对这些材料进行快速的拓扑分类,最终得到10897个有趣的材料,其中包含1123 个拓扑绝缘体,709 个拓扑晶体绝缘体和9065 个在费米面附近存在能带交点的体系(材料的结构和能带信息见ccmp.nju.edu.cn)。如图5 所示,大规模搜索结果表明拓扑材料并非人们以前认为的那么罕见[90]。
图5 ICSD晶体库拓扑材料大规模搜索结果统计[90]


下面将分析我们找到的几个典型的拓扑材料来进一步展示如何利用对称性指标来判断各种各样的拓扑材料,以及在得到拓扑归类以后所需的进一步分析。
6.1 拓扑晶体绝缘体
利用拓扑材料搜索方案,我们发现MoTe2(SG11)和BiBr(SG12)可以分别实现图6(a)中“2”对应的两个拓扑晶体绝缘体相。有关这2 个材料体系的具体讨论如下:
MoTe2具有3个不同的晶体结构:六角α 相[95],单斜β相[96]以及正交γ 相[97]。在室温下的结构为β-MoTe2。其单层被预言可以实现量子自旋霍尔绝缘体[59]。在240—260 K左右,结构相变使其变成非中心反演对称的γ 相,这个相被理论预言为type-IIWeyl半金属并被实验证实[98—100]。
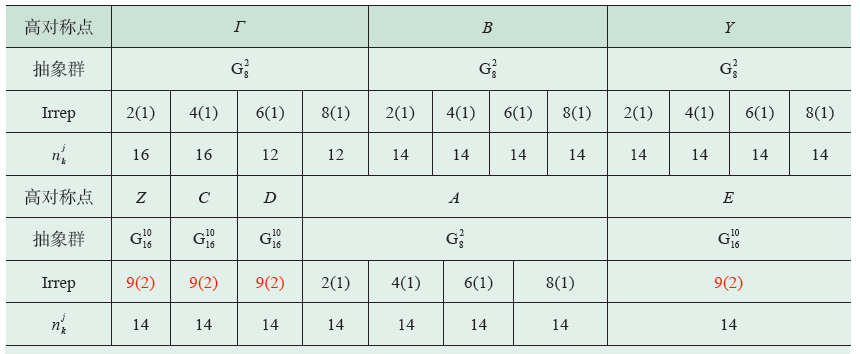
β-MoTe2具有单斜层状结构,属于SG11,其初基元胞内包含4 个Mo以及8 个Te 原子,均占据在SG11 的2eWyckoff 位置,一个元胞内价电子数为56。我们把第11 号空间群独立的高对称点、其对应的不可约表示列在表2 中。在表2 中也列出了密度泛函计算得到的β-MoTe2价带在BZ高对称点Γ,B,Y,Z,C,D,A,E上不可约表示的占据数情况, 从而得到了n=(56, 16, 16, 12,12, 14, 14, 14, 14, 14, 14, 14, 14, 14,14,14,14,14,14,14,14)。把计算得到的n对于SG11 的5 个原子绝缘体基矢(原子绝缘体基组见文献[90]中的补充材料)做式(7)状展开,得到展开系数为( q1,q2,q3,q4,q5 )=(12,2,1,1,1/2)。它属于情形(ii),且SI=(0,0,2) (SG11 的XBS = Z2 × Z2 × Z4 ),因此它一定是拓扑晶体绝缘体。
表2 β-MoTe2的56 个价带在高对称点Γ,B,Y,Z,C,D,A,E上不可约表示的占据数,根据文献[89],我们也展示了这些高对称点的对称群从属的抽象群,同时根据抽象群不可约表示给出小群不可约表示,比如Γ点的第一个不可约表示为抽象群G82 的第2 个不可约表示。在Irrep 行中,括号里数字标记维度。受到时间反演对称性的要求,Z,C,D和E 唯一一个2 维不可约表示必须成对出现(表中以红色显示了这些表示),因此相应的占据数应该表示为一对这样的表示所出现的次数,比如Z 点的不可约表示出现28 次,但是考虑时间反演对称的要求,计算得到的占据数(即时间反演对的占据数)为14
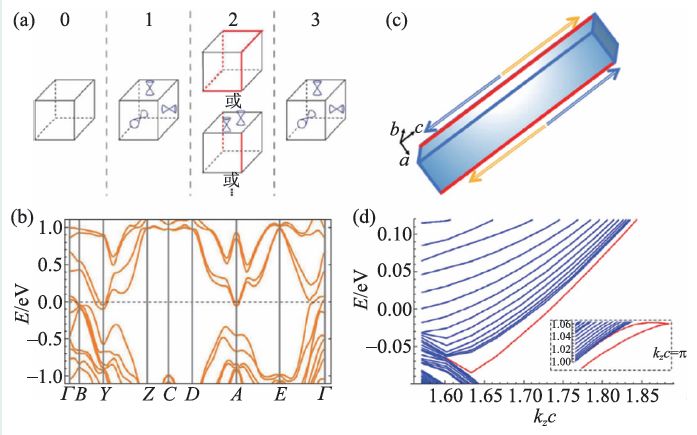
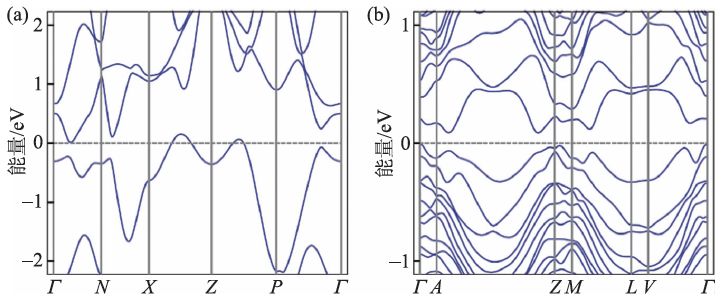
图6 (a)Z4强SI 群中不同取值对应的拓扑相;(b)MoTe2(SG11)的电子能带结构;(c)为了计算螺旋对称保护的铰链态,我们取了在a 和b 方向有界的棱柱,在c 方向取周期性边界条件;(d)图(c)中棱柱的电子结构,其中红色表示铰链态,它们的实空间分布在(c)中示意地表示,其中箭头表示铰链态运动方向,不同颜色表示相反自旋
如图6(b)所示,β-MoTe2虽然具有一定的费米面,但是在整个BZ 中处处存在有限的直接带隙,因此其拓扑不变量是有定义的。这里的SI 可对应于两种拓扑保护的边界态:镜面保护的表面态或者螺旋轴保护的铰链态, 为此需要计算β-MoTe2的镜面陈数[92,93]。直接通过第一性原理计算发现kz=0 和π/c面的镜面陈数都为0,所以这个材料对应的就一定是螺旋对称保护的拓扑晶体绝缘体[92,93],可以实现拓扑保护的一维铰链态。
为了验证上述高阶绝缘体特有的“体—边”对应,我们构建了同时具有空间反演和螺旋对称的棱柱(图6(c)),并且计算了棱柱的电子结构,如图6(d)所示,根据波函数实空间的分布区分出来铰链态,在图6(d)中以红线表示(两个helical 的铰链态在棱柱中的具体位置见图6(c)。值得提及的是,这里的结果被Wang等人的工作证实[101]。
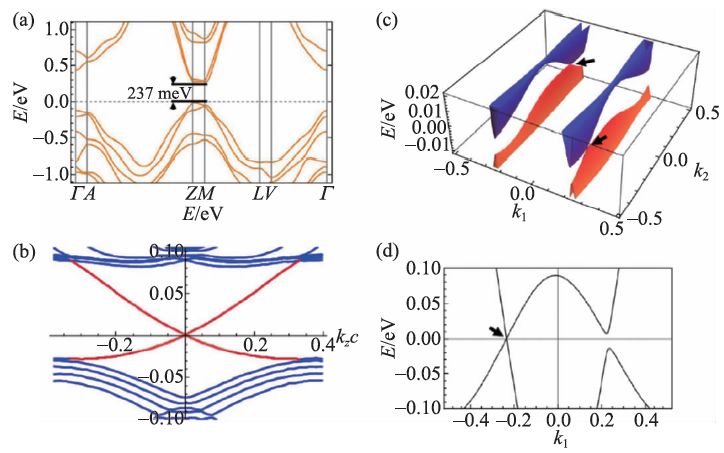
BiBr 属于SG12。与SG11(具有螺旋对称)相比,SG12 具有旋转操作(二度旋转C2),可实现人们提出的旋转反转[102],即在C2对称的表面上实现Dirac 表面态。如图7(a)所示,计算表明BiBr 具有0.24 eV左右的带隙。第一性原理计算发现,BiBr的SI=(0,0,2) (SG12 的XBS = Z2 × Z2 × Z4 ),这说明这个材料是受到晶格对称保护的拓扑晶体绝缘体。但是仅仅从SI,还无法确定BiBr 的拓扑性质,因为它的拓扑保护的表面态可能受到镜面保护。通过计算kz=0 和π/c面上的镜面陈数,发现它们均为0,因此BiBr 中存在受到C2 保护的表面态,可以实现旋转反常[92,93,102]。理论计算发现,这种表面态出现在表面BZ中的一般点坐标(在表面倒格矢基组下)为(k1D ,k2D)= ±(-0.237,0.333) ,如图7(c)和(d)所示。同时,跟MoTe2(SG11)一样,BiBr(SG12)也可以具有一维铰链态,也即是图6(a)中所示的情形:铰链态和旋转保护的表面态共存。这里的铰链态受到空间反演保护,我们取了具有类似对称性的棱柱,计算得到一维铰链态的电子能带色散如图7(b)所示。这些预言得到了最近工作的证实[103]。
图7 (a)BiBr(SG12)的电子能带结构;(b)取中心反演对称的BiBr 棱柱,计算得到沿着c 方向的铰链态(红色)的色散,类似于β-MoTe2,这些铰链态局域在C2联系起来的两个相对的铰链上;(c)在C2对称的(001)面上出现的Dirac型表面态,其Dirac点在表面BZ中的一般位置(黑色箭头处);(d)图(c)中经过Dirac 点的一维路径(k2=0.333)上的能带色散,可以清楚地看到Dirac的位置(黑色箭头处,k1=-0.237)
除了上面两个材料,我们也发现了数百种拓扑晶体绝缘体材料[90], 其中SG164 的Bi2Se2 和Bi2Pb2Te5具有较大的体能隙( ≥ 25 meV )。尤其需要指出的是,其中除了上述Z4 SI 群的体系,高阶SI 群(Z8,Z12)体系的拓扑材料也非常有意思[91],相对于Z4群的材料,这些材料的SI 可以取更多的值,同时由于存在着丰富的晶格对称性,这些材料具有多种晶格对称保护的表面态/铰链态,这些具体的材料有助于将来研究这些边界态之间相互作用或者在外界微扰下,不同边界态的演化等带来的有意思的物理现象。石墨(SG194)可以看成是石墨烯的ABABABAB…Bernal 型堆积,我们计算发现其SI=(4)(SG194 的XBS=Z12)。根据第一性原理计算结果,SOC在K/K'打开了约为0.025 meV 的体能隙。我们使用第一性原理方法计算了kz=0 和π/c面的镜面陈数,发现后者为0,前者为-2。进一步计算平面的镜面陈数,发现为0。因此石墨可以呈现6 重螺旋对称保护的铰链态[92,93],同时受到(010)滑移对称和
旋转对称的保护,石墨分别可以呈现沙漏型表面态和旋转反常。对于SG140(XBS=Z2×Z8)的Pt3Ge,计算发现其SI 为(0,4),同时(001)和(110)镜面对称对应的镜面陈数都为0,这说明这个材料在(100)滑移面上可以具有拓扑保护的沙漏型表面态,在c 方向存在受4 度螺旋对称保护的1 维铰链态。
6.2 拓扑绝缘体
下面给出拓扑绝缘体(或叫强拓扑绝缘体)的一些例子。SG139的SI群为XBS = Z2 × Z8 。根据第一性原理计算可得,Ag2Zr(SG139)的SI=(0,1)。这说明Ag2Zr(SG139)是一个(强)拓扑绝缘体。如图8(a)所示,Ag2Zr(SG139)的费米面穿过一些能带,该材料具有一定的费米口袋,但是我们发现费米口袋的体积比较小,这说明在适当的动量—能量窗口下,人们可以观测到拓扑保护的Dirac 型表面态的色散。我们也发现了一些具有能隙的拓扑绝缘体,比如Ba11Cd14Bi8(SG12),其电子能带结构如图8(b)所示。第一性原理计算发现它具有大约34 meV 左右的能隙,大于室温对应的热激发能(25 meV),从而这个拓扑绝缘体材料也是值得进一步研究的。
图8 (a) 拓扑绝缘体Ag2Zr(SG139) 的电子能带结构;(b) 拓扑绝缘体Ba11Cd14Bi8(SG12)的电子能带结构
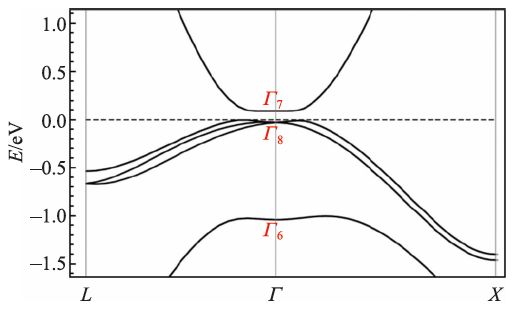
上面两个材料都是具有中心反演对称的,其Z2拓扑不变量可以直接根据宇称进行计算。而具有Z2 SI 群的体系[87],虽然没有中心反演对称,但是具有S4(= C4σh )对称。通常人们需要计算波函数的内积来得到Z2拓扑不变量[81],或者通过绝热连接得到中心反演对称的体系,计算中心反演对称体系的宇称来得到原来体系的Z2拓扑不变量。而这里,直接计算Z2 SI 群中的取值(=2q mod 2=0或1,其中q 为价带n 在公因子为2 的AI 基矢上展开系数),就能够迅速得到这些空间群下材料是否为拓扑绝缘体的判断。我们在图9 中展示了AgNaO(SG216)的电子结构,作为这种拓扑绝缘体的例子。SG216 没有中心反演对称操作,但是它具有S4对称,拥有6 个原子绝缘体基矢,仅仅最后一个原子绝缘体基矢具有公因子为2,其余公因子为1。我们发现该材料的SI=1,因此该材料一定是拓扑绝缘体。而这个拓扑绝缘体相也可以从能带反转的图像理解:如图9 所示,s 带主要出现在在费米面上面,而d 带主要出现在费米面下面。但是在Γ点,Γ6(具有s 带成分)在Γ7(具有d带成分)下方。实际上,这里的拓扑绝缘体性质也可以通过计算S4不变的动量上S4本征态占据数来计算S4拓扑不变量κ4[92,93]:
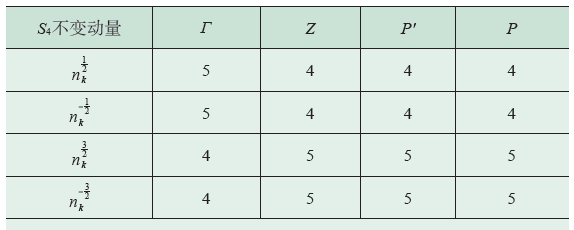
其中SIM指S4不变的动量(即具有S4对称的高对称点)集合,这里对于SG216,SIM={ Γ,Z,P',P}( 见表3), s4 是S4 的本征值, 且s4= exp(-ijzπ/2) ( jz = 1/2,- 1/2, 3/2, - 3/2)。第一性计算得到κ4 = 1mod 2 (参见表3),表明材料是一个强拓扑绝缘体[92,93]。
图9 AgNaO(SG216)的电子能带结构,其中Γ6,Γ7,Γ8 标记Γ 点的不可约表示,昭示了能带反转的特征
表3 AgNaO价带在S4本征值中的占据数,其中nkjz 中jz = 1/2, - 1/2, 3/2, - 3/2用来标记S4本征值, exp(-ijzπ/2) 。Γ=(0, 0, 0),Z=(0,0,1),P' =(0, 1, -1/2),P=(0,1,1/2),为4 个S4不变动量的坐标(在惯用元胞对应的倒空间基矢下)
在文献[90]中我们也列出一些潜在的适合应用的拓扑绝缘体材料,它们的能隙大于室温对应的热激发能(~25 meV),如表4所示。
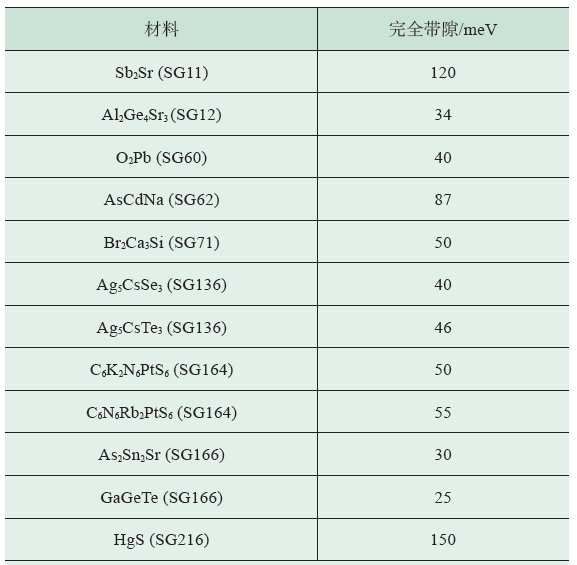
表4 我们预言的一些具有较大能隙(≥25 meV)的拓扑绝缘体材料,在“材料”列中,每一个化学式后面给出了所在的空间群
6.3 Dirac半金属
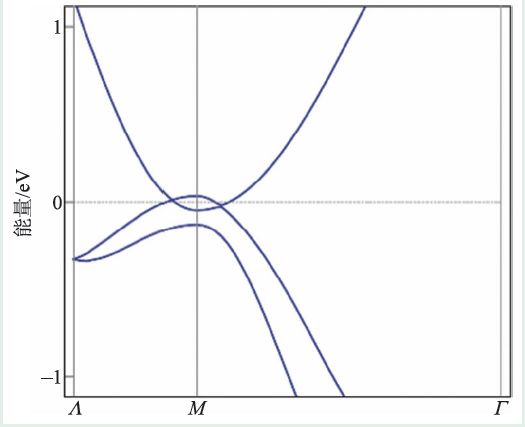
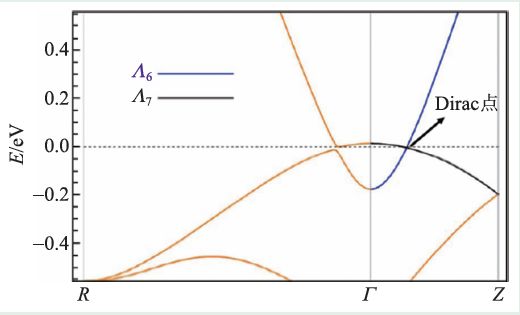
我们也发现了大量半金属材料,这里展示费米面几乎只穿过狄拉克点的两个材料:OPd(SG131)[90]和MgBi2O6(SG136)[88]。第一性原理计算得到的n都是整数,表明这些材料所有高对称点上均具有有限的直接带隙。而根据(7)式做展开,发现展开系数满足情形(iii),进一步分析发现材料属于情形(iii)的第2 个子情形。这样这两个材料均在高对称线/面上有对称性保护能带交叉点。进一步分析得知,这两个材料的能带交点为位于高对称线上的Dirac 点,如图10 和11 所示,均受C4v保护。除此之外,在文献[92]和[104]中,我们也得到了一些比较干净的Dirac 半金属,将这些材料以及Dirac点的位置列于表5中。
表5 一些费米面比较干净且Dirac 点离费米面较近的Dirac 材料[91,104],这里除了给出空间群(SG)信息、材料化学式,还给出了Dirac 点的位置(它们可以在高对称点上,比如K3Pt2O4的Z,T,R 上,或者高对称线上,比如Al3Nb的Γ-Z线上)
图10 Dirac半金属OPd(SG131)的电子能带图
图11 Dirac 半金属MgBi2O6(SG136)的电子结构,其中箭头标记Dirac 点, Λ6 和Λ7 标记高对称线Γ - Z 上两个不同不可约表示


本文详细地介绍了我们基于对称性指标理论,发展的使用原子绝缘体基组高效判断材料拓扑性质的方法,以及使用该算法对非磁性材料库进行拓扑筛选的结果(见ccmp.nju.edu.cn)。值得提及的是,中国科学院物理研究所方辰、翁红明、方忠团队[105]和普林斯顿Benervig,Zhijun Wang 团队[106]分别利用对称性指标[93,107]和图论方法[86]进行了晶体库的拓扑材料搜索,并且分别在http://materiae.iphy.ac.cn/[105] 和https://www.topologicalquantumchemistry.com/[106]中列出了所有发现的拓扑材料。在这些材料中,找寻性能优越具有潜在应用前景的拓扑材料将是一件非常有意思的课题。
文中介绍的方案也可以应用到二维材料,也就是需要考虑80 个layer 群[108]。此外,考虑磁性材料,该方案还可以被应用到1651 个磁性空间群[109]。除了稳定的拓扑,情形(i)中还可能存在不稳定的,所谓“易碎的”拓扑[110],寻找具有这类拓扑的材料实现也非常有意思,而相关算法也可以很容易基于原子绝缘体基组来实现。此外,我们的方法对于构建具有期望拓扑性质的有效模型(全BZ)也非常有用。除了上述单电子图像下的拓扑性质,考虑多电子相互作用的拓扑材料的寻找也值得作为未来进一步的课题。
另外, 除了电子拓扑材料, 近年来, 光子、声子、磁振子等玻色系统的拓扑性质也引来了很多研究兴趣,而光子的空间群理论[111,112]也已经被提出来。基于对称性指标寻找实现拓扑超导的材料[113],也是未来非常值得研究的课题。
计算方法说明
我们的第一性电子结构计算基于WIEN2k 软件[114],并且考虑自旋轨道耦合,使用了Perdew—Burke—Ernzerhof (PBE)采取广义梯度近似(GGA)的交换关联势[115]。在文献[90]中对挑选的好的拓扑(晶体)绝缘体进行了进一步mBJ (modifiedBecke—Johnson)[116]计算。
致谢 感谢Ashvin Vishwanath 和Hoi ChunPo在系列工作[88,90,91]中的合作。
参考文献
[1] v Klitzing K,Dorda G,Pepper M. Phys. Rev. Lett.,1980,45:494
[2] Thouless D J,Kohmoto M,Nightingale M P et al. Phys. Rev.Lett.,1982,49:405
[3] Haldane F D M. Phys. Rev. Lett.,1988,61:2015
[4] Hasan M Z,Kane C L. Rev. Mod. Phys.,2010,82:3045
[5] Qi X L,Zhang S C. Rev. Mod. Phys.,2011,83:1057
[6] Kane C L,Mele E J. Phys. Rev. Lett.,2005,95:226801
[7] Kane C L,Mele E J. Phys. Rev. Lett.,2005,95:146802
[8] Bernevig B A,Hughes T,Zhang S C. Science,2006,314:1757
[9] Fu L,Kane C L,Kane E J. Phy. Rev. Lett.,2007,98:106803
[10] Moore J E,Balents L. Phys. Rev. B,2007,75:121306 (R)
[11] Roy R. Phys. Rev. B,2009,79:195322
[12] Schnyder A P,Ryu S,Furusaki A et al. Phys. Rev. B,2008,78:195125
[13] Ryu S,Schnyder A P,Furusaki A et al. New Journal of Physics,2010,12:065010
[14] Kitaev A. AIP Conference Proceedings,2009,1134:22
[15] Chiu C K,Teo J C Y,Schnyder A P et al. Rev. Mod. Phys.,2016,88:035005
[16] Fu L. Phys. Rev. Lett.,2011,106:106802
[17] Hsieh T H,Lin H,Liu J et al. Nature Commun.,2012,3:982
[18] Wang Z,Alexandradinata A,Cava R J et al. Nature,2016,532:189
[19]Wieder B J et al. Science,2018,361:246
[20] Schindler F et al. Science Advances,2018,4:eaat0346
[21] Benalcazar W A,Bernevig B A,Hughes T L. Science,2017,357:61
[22] Benalcazar W A,Bernevig B A,Hughes T L. Phys. Rev. B,2017,96:245115
[23] Song Z,Fang Z,Fang C. Phys. Rev. Lett.,2017,119:246402
[24] Langbehn J,Peng Y,Trifunovic L et al. Phys. Rev. Lett.,2017,119:246401
[25] Slager R J,Mesarosm A,Juričic V et al. Nature Physics,2013,9:98
[26] Ando Y,Fu L. Annu. Rev. Condens. Matter Phys.,2015,6:361
[27] Wan X,Turner AM,Vishwanath A et al. Phys. Rev. B,2011,83:205101;万贤纲. 物理,2015,44:427
[28] Young S M,Zaheer S,Teo J C Y et al. Phys. Rev. Lett.,2012,108:140405
[29]Wang Z et al. Phys. Rev. B,2012,85:195320
[30]Wang Z,Weng H,Wu Q et al. Phys. Rev. B,2013,88:125427
[31] Burkov A A,Hook M D,Balents L. Phys. Rev. B,2011,84:235126
[32] Weng H,Liang Y,Xu Q et al. Phys. Rev. B,2015,92:045108;Fang C,Chen Y,Kee H Y et al. Phys. Rev. B,2015,92:081201
[33] Bzdusek T,Wu Q S,Ruegg A et al. Nature,2016,538:75
[34] Chen W,Lu H Z,Hou J M. Phys. Rev. B,2017,96:041102(R);Sun X Q,Lian B,Zhang S C. Phys. Rev. Lett.,2017,119:147001;Yan Z,Bi R,Shen H et al. Phys. Rev. B,2017,96:041103(R)
[35] Chang PY,Yee C H. Phys. Rev. B,2017,96:081114(R)
[36] Ezawa M. Phys. Rev. B,2017,96:041202(R)
[37]Wang L,Jian S K,Yao H. Phys. Rev. B,2017,96:075110
[38] Bradlyn B et al. Science,2016,353:aaf5037;Weng H,Fang C,Fang Z et al. Phys. Rev. B,2016,93:241202(R);Weng H,FangC,Fang Z et al. Phys. Rev. B,2016,94:165201
[39] Zhang T et al. Phys. Rev. Lett.,2009,103:266803
[40] Fu L,Kane C L. Phys. Rev. Lett.,2008,100:096407;AkhmerovA R,Nilsson J,Beenakker C W J. Phys. Rev. Lett.,2009,102:216404
[41] Qi X L,Hughes T L,Zhang S C. Phys. Rev. B,2008,78:195424;Essin A,Moore J E,Vanderbilt D. Phys. Rev. Lett.,2009,102:146805
[42] Son D T,Spivak B Z. Phys. Rev. B,2013,88:104412
[43] Potter A C,Kimchi I,Vishwanath A. Nature Commun.,2014,5:5161'· 354 ··48卷(2019 年) 6 期
[44] Wang C M,Sun H P,Lu H Z et al. Phys. Rev. Lett.,2017,119:136806
[45] Zhang C et al. Nature,2019,565:331
[46] Yang K Y,Lu YM,Ran Y. Phys. Rev. B,2011,84:075129
[47] Hosur P,Dai X,Fang Z et al. Phys. Rev. B,2014,90:045130
[48]Wu L et al. Nature Physics,2017,13:350
[49] Katsnelson M I,Novoselov K S,Geim A K. Nature Physics,2006,2:620
[50] Kopnin N B,Heikkila T T,Volovik G E. Phys. Rev. B,2011,83:220503(R)
[51] Zhang H,Liu C X,Qi X L et al. Nature Physics,2009,5:438
[52] Weng H,Fang C,Fang Z et al. Phys. Rev. X,2015,5:011029;Huang S M et al. Nature Commun.,2015,6:7373
[53] Xu G,Weng H,Wang Z et al. Phys. Rev. Lett.,2011,107:186806
[54] Yu R,Weng H,Fang Z et al. Phys. Rev. Lett.,2015,115:036807;Kim Y,Wieder B J,Kane C L et al. Phys. Rev. Lett.,2015,115:036806
[55] Yu R,ZhangW,Zhang H J et al. Science,2010,329:61
[56] Du Y,Wan B,Wang D et al. Scientific Reports,2015,5:14423;Du Y et al. npj Quantum Materials,2017,2:3
[57] Liu C C,FengW,Yao Y. Phys. Rev. Lett.,2011,107:076802
[58] Zhang H J et al. Phys. Rev. Lett.,2011,106:156402
[59] Qian X,Liu J,Fu L et al. Science,2014,346:1344
[60] ZhangWet al. Phys. Rev. Lett.,2011,106:156808
[61] Neupane M et al. Phys. Rev. B,2012,85:235406
[62] Kuroda K et al. Phys. Rev. Lett.,2012,108:206803
[63] Yan B et al. Europhys. Lett.,2010,90:37002
[64] Sato T et al. Phys. Rev. Lett.,2010,105:136802
[65] Xu Y et al. Phys. Rev. Lett.,2013,111:136804
[66] Bansil A,Lin H,Das T. Rev. Mod. Phys.,2016,88:021004
[67] Tang P,Zhou Q,Zhang S C. Phys. Rev. Lett.,2017,119:206402
[68] Schindler F et al. Nature Physics,2018,14:918
[69] Hsieh D et al. Nature,2009,460:1101;Chen Y et al. Science,2009,325:178;Xia Y et al. Nature Physics,2009,5:398
[70] Liu Z K et al. Science,2014,343:864;Liu Z K et al. Nature Materials,2014,13:677
[71] Lv B Q et al. Phys. Rev. X,2015,5:031013;Xu S Y et al. Science,2015,349:613;Lv B Q et al. Nature,2017,546:627
[72] Zhang C L et al. Nature Commun.,2016,7:10735;Huang Xet al. Phys. Rev. X,2015,5:031023
[73] Fei Z et al. Nature Physics,2017,13:677;Tang S et al. NaturePhysics,2017,13:683
[74] Zhu F F et al. Nature Materials,2015,14:1020
[75] Chang C Z et al. Science,2013,340:167
[76] Takane D et al. Phys. Rev. Lett.,2019,122:076402
[77] Rao Z et al. Nature,2019,567:496
[78] Sanchez D S et al. Nature,2019,567:500
[79] Ando Y. J. Phys. Soc. Jpn.,2013,82:102001
[80] Armitage N P,Mele E J,Vishwanath A. Rev. Mod. Phys.,2018,90:015001
[81] Feng W,Wen J,Zhou J et al. Computer Physics Communications,2012,183:1849
[82] Scanlon D O et al. Adv. Mater.,2012,24:2154
[83]Wang N et al. Phys. Rev. B,2014,89:045142
[84] Fu L,Kane C L. Phys. Rev. B,2007,76:045302
[85] Fang C,Gilbert M J,Bernevig B A. Phys. Rev. B,2012,86:115112
[86] Bradlyn B,Elcoro L,Cano J et al. Nature,2017,547:298
[87] Po H C,Vishwanath A,Watanabe H. Nature Commun.,2017,8:50
[88] Tang F,Po H C,Vishwanath A et al. Nature Physics,2019,15:470
[89] Bradley C J,Cracknell A P. The Mathematical Theory of Symmetryin Solids:Representation Theory for Point Groups andSpace Groups. Oxford University Press,1972
[90] Tang F,Po H C,Vishwanath A et al. Nature,2019,566:486
[91] Tang F,Po H C,Vishwanath A et al. Science Advances,2019,5:eaau8725
[92] Khalaf E,Po H C,Vishwanath A et al. Phys. Rev. X,2018,8:031070
[93] Song Z,Zhang T,Fang Z et al. Nature Commun.,2018,9:3530
[94] Hellenbrandt M. Crystallogr. Rev.,2004,10:17
[95] Brixner L H. J. Inorg. Nucl. Chem.,1962,24:257
[96] Brown B E. Acta Crystallogr.,1966,20:268
[97] Clarke R,Marseglia E,Hughes H P. Philos. Mag. B,1978,38:121
[98] Deng K et al. Nature Physics,2016,12:1105
[99] Tamai A et al. Phys. Rev. X,2016,6:031021
[100] Huang L et al. Nat. Mater.,2016,15:1155;Jiang J et al. Nat.Commun.,2017,8:13973
[101]Wang Z,Wieder B J,Li J et al. arXiv 1806.11116 (2018)
[102] Fang C,Fu L. arXiv 1709.01929 (2017)
[103] Hsu C H et al. 2D Mater.,2019,6:031004· 355 ·评述·48卷(2019 年) 6 期
[104] Tang F,Wan X. Frontiers of Physics,2019,14:4
[105] Zhang T,Jiang Y,Song Z et al. Nature,2019,566:475
[106] Vergniory M G,Elcoro L,Felser C et al. Nature,2019,566:480
[107] Song Z,Zhang T,Fang C. Phys. Rev. X,2018,8:031069
[108]Wang D et al. arXiv 1906. 01283 (2019)
[109] Watanabe H,Po H C,Vishwanath A. Science Advances,2018,4:eaat8685
[110] Po H C,Watanabe H,Vishwanath A. Phys. Rev. Lett.,2018,121:126402
[111]Watanabe H,Lu L. Phys. Rev. Lett.,2018,121:263903
[112] de Paz M B,Vergniory M G,Bercioux D et al. arXiv 1903.02562 (2019)
[113] Ono S,Yanase Y,Watanabe H. arXiv 1811.08712 (2018)
[114] Blaha P,Schwarz K,Madsen G K H et al. WIEN2k:An AugmentedPlane Wave + Local Orbitals Program for CalculatingCrystal Properties. Karlheinz Schwarz,Technische Univ. Wien,Autria,2001
[115] Perdew J P,Burke K,Ernzerhof M. Phys. Rev. Lett.,1996,77:3865
[116] Koller D,Tran F,Blaha P. Phys. Rev. B,2001,83:195134
本文选自《物理》2019年第6期
3.现实中的“降维攻击”导致二维拓扑量子物态 | 文小刚点评
5.特别二的物理学——节选自《物理学咬文嚼字》彩色四卷本全集
10.周光召先生与开放的中科院理论物理所 | 贺周光召先生从事科学事业65周年