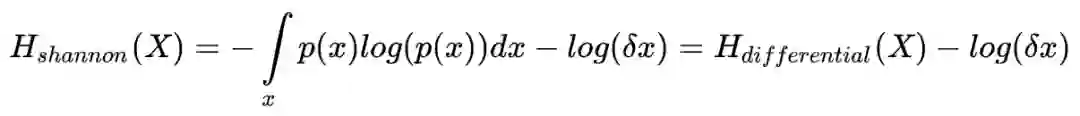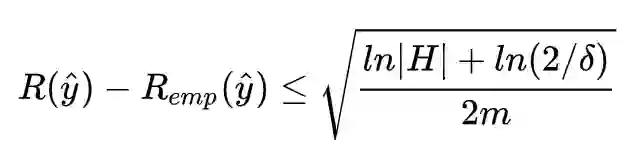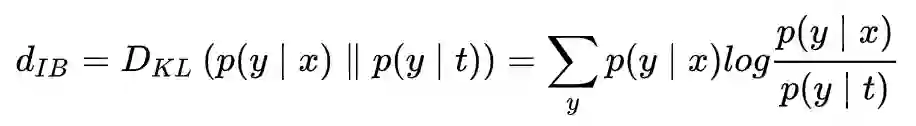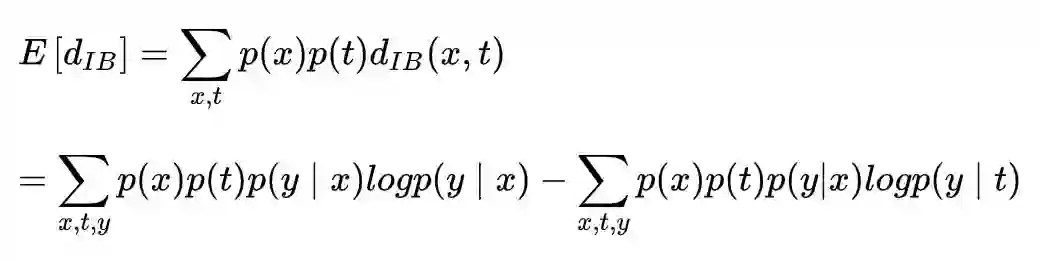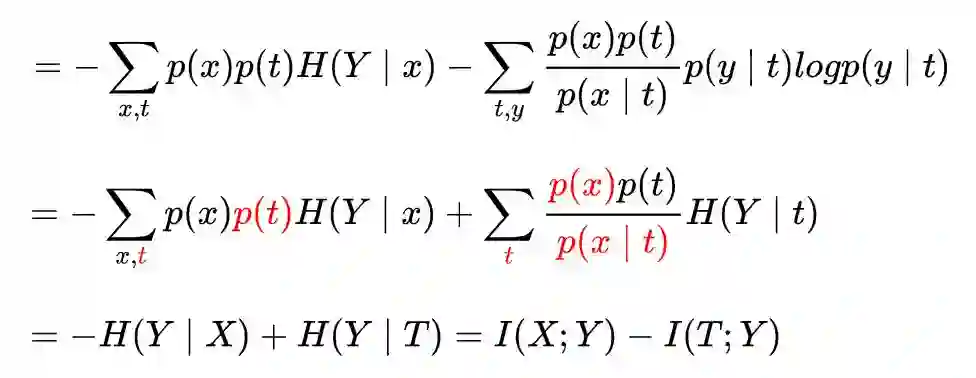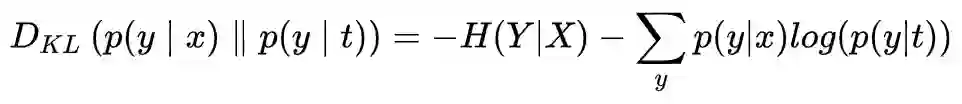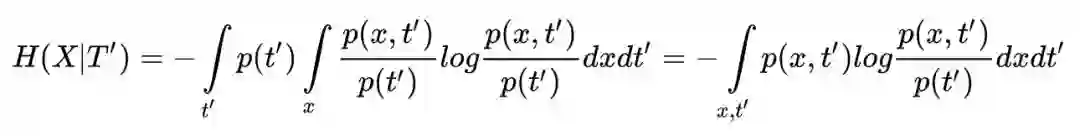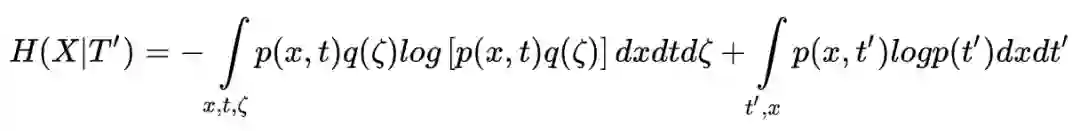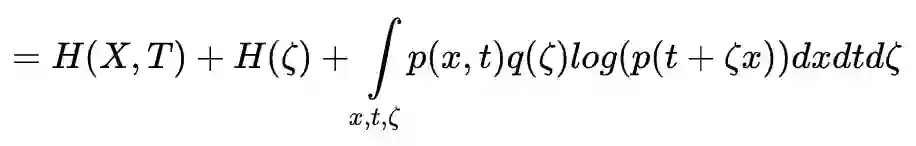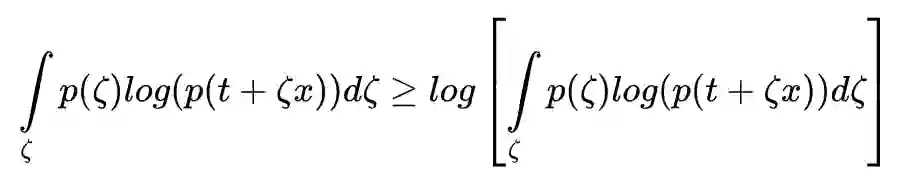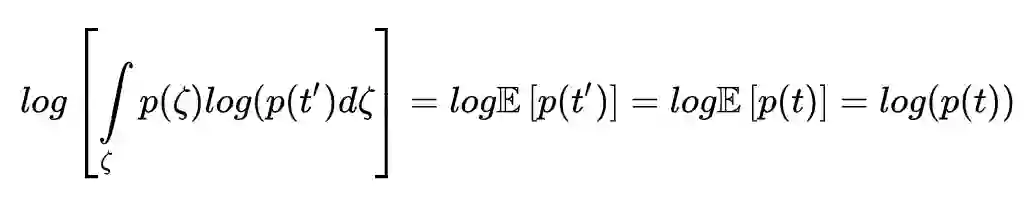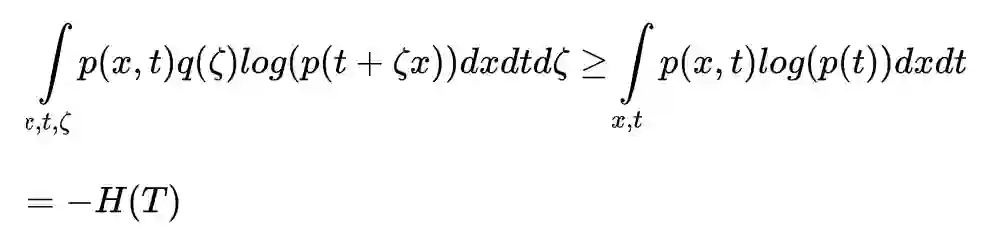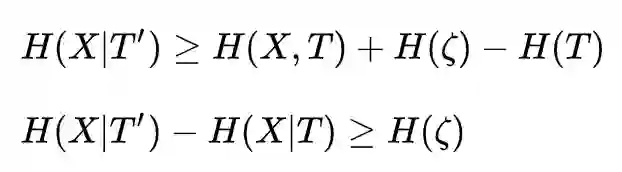从信息瓶颈理论一瞥机器学习的“大一统理论”
作者丨哈啾路亚
单位丨顺丰科技
研究方向丨NLP,神经网络
个人主页丨http://st-time.space
序言
所有机器学习的原理,本质上都是对同一段信息在不同空间内的转换、过滤、重新表征,最终解码出一段可读信息。为了让最终信息可读,我们需要给最终输出的每一个 bit 赋予意义。如果是监督学习,则需要定义一个度量来描述输出信息与真实信息的距离。
列举常见的传统机器学习,我们可以发现大多数监督学习都遵循着这一机制。
SVM 使用内核机制重新定义了两个向量的内积,经过 centering 这样一个定义原点的操作之后,可以很快看出内核机制实际上重新定义了两个样本间的欧式距离。
而任意两点间的欧式距离被改变,则意味着坐标系的转换,并且转换过后的新坐标系基本上不再是直角坐标系了,很可能是一个更高或是更低维度流型上的曲线坐标系。这时优化度量 margin loss 再在新坐标系上尝试分割出正负样本的 support vector 的最大间隔,找到线性超平面即可。
所有回归,包括线性回归、回归树,以及各种 boosting tree,其坐标转换部分也非常明显,从 N 维输入到 1 维输出的转换(不管线性还是非线性),之后接一个优化度量(KL 距离既交叉熵、最小二乘、triplet loss,etc.)。
贝叶斯流派的最终优化目标:logP(x),其本质还是减少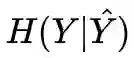
那么,除了输入与输出的表征方法,以及优化度量的选择之外,是否在各种机器学习包括深度学习方法内,通用的一些规则呢?就如同牛顿三大定律一样,足以解释所有经典力学的公式。
从信息瓶颈方法出发,接下来会尝试解释一系列深度学习中出现的知识,并稍作延伸与传统学习的知识点进行类比,去探索机器学习的最核心思路。
何为信息
以一个二值编码的 10 维向量为例,其排列组合个数 2^10=1024,根据香农熵的定义,一个 10 维 binary 向量的最大可承载信息量是 log(1024) = 10 。
同样是 10 维,假如不是 binary,而是任意连续变量,那么有两种方法可以用来估算连续变量的熵:分箱法以及基于 knn 的估算,后者本质上是一种不均匀的分箱法,所以就拿分箱法举例,假如同样是 0-1 区间被分成 20 个区间,那么该 10 维向量的最大可承载信息量就是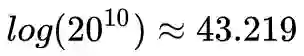
一个分布 X,如果满足 10 维随机均匀分布,那么其混乱度最大,能够达到最大可承载信息。实际上无论是任何分布,只要出现更粗粒度的离散化操作,其熵 H(X) 必然会不可逆地减少,出现信息损失。
我们通常定义下的熵是微分熵,与香农熵的关系仅相差了一项与分箱间隔 δx 相关的一项。这项可以被当作常量,比如 float 数据类型的 epsilon error,所以后面的熵统一以 H 代替,不指明是香农还是微分熵了。
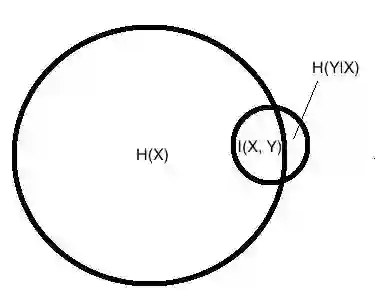
输入分布 X 内包含的所有信息,我们写作 H(X) ,然而我需要抽取的信号一般要小很多,这样才方便解读。我们的优化目标希望预测分布
与目标分布 Y 的距离(KL 或 Eucledian)越小越好。目标与输入的互信息 I(X,Y) 是有用的,而其他信息 H(X|Y) 以及 H(Y|X) 是无用的,因为我们无法解读它们。
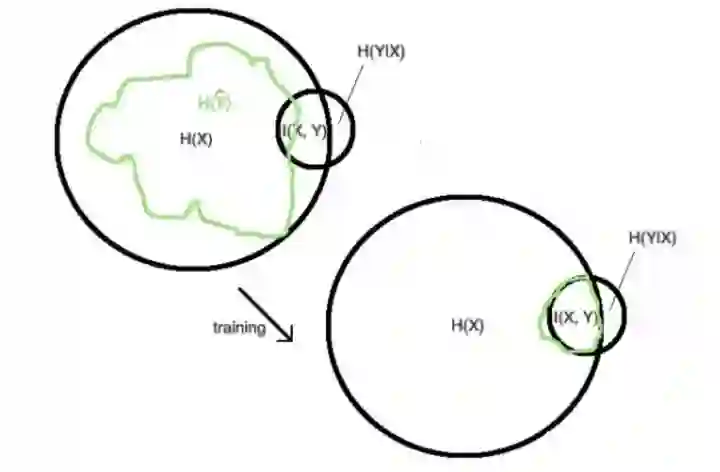
训练的最终目标是我们的内包含的信息,从最初随机权重得到的绿色区域信息,逐渐遗忘掉 X 里与 Y 不相关的信息,同时尽量捕捉到 X 里与 Y 相关的信息。
增加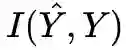
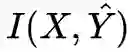
这里泛化误差上界 generalization error bound 的推导,需要从霍夫丁不等式开始,具体细节就不展开了,感兴趣的可以网上搜推导过程。
要以置信度 δ 来确保样本分布 emp 与真实分布的预测值的差的绝对值不大于一个范化误差上界,有两种最有效方法:增加样本数量 m 或是减少的可取值的数量 |H| 。
注意到信息量与 |H| 不相等,但是是有正相关性的。越有秩序的
,其可能的取值个数(分箱过后)|H| 越小,且最大值不可能超过向量
的信息承载上限。
这样一来,只要减少,我们就能获得更优的范化误差表现,避免模型过拟合。不仅是在输出特征
上需要进行压缩(尽量在保证
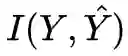
举个例子,当我需要判定一辆车是否能在机动车道行驶,我只需要知道车有 4 个轮子还是 2 个轮子就够了,不需要特征告诉我“有一辆蓝色 4 个轮子的车能够上机动车道”、“有一辆黑色 4 个轮子的车能够上机动车道”、“有一辆白色 2 个轮子的车不能上机动车道”……我不需要颜色这种不相关的信息,所以让特征层在进行特征变换时尽早遗忘掉颜色吧,这样还能节省一些训练需要的样本数。
信息瓶颈的实现方法
通过上面的简单论证,得到了要想用有限的样本取得更小范化误差,同时让预测结果尽量接近真实目标,就需要最大化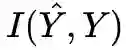
或是 |H| ,那么接下来就分析一下哪些操作能够实现上面两个目标吧。
假设 t=任意特征值,可以是输出层,也可以是任何一个传递信息的中间层。
考虑上面 KL 距离的预期值:
使用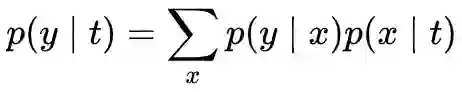
X 和 Y 的互信息取决于样本集,是个常量,所以训练过程中,逐渐减少:
就可以增加 I(T, Y)。
再次忽略常量 -H(Y|X),可以看到减少交叉熵,就是增加互信息 I(T, Y)。
学习的目标是由优化度量直接决定的,最小二乘的极小值也是类似的情况。
要压缩 H(T) ,可动用的手段就非常多了。一种方法是对信息的载体——向量,在其上面动手脚。
drop out按一定比例直接砍;
max pooling可以砍大约一半的 H(T);
离散化大杀器,直接砍 H(T) 上限到一个指定数值,一般用在模型最后 argmax 操作上。
L2 正则以及 batch normalization 都间接或直接地限制了 t 值的取值范围,使相同分箱间隔下, |H| 被指数级减少。
还有一种隐藏比较深但是更加常见的压缩方法,就是在梯度上增加噪音。梯度上的噪音会通过牛顿下降直接传到权重更新 Δw 上。
明明目标是要去除 H(T) 里的无用信息,为何要在权重更新 Δw 上添加噪音呢?这里就需要一些推理思考了。
信噪比:科学训练的关键
首先我们需要定义信号与噪音。
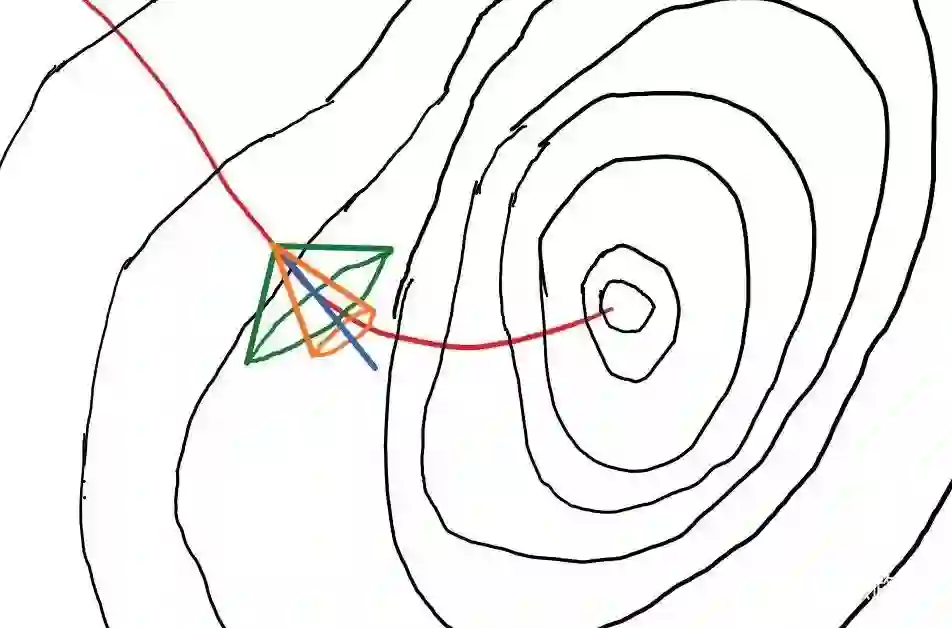
▲ 等高线描述了Loss(W, x)在x等于真实分布X时的预期值=const,写作L(W)=const
梯度下降时,完全无噪音的下降路径,应该在下降路径中时刻保持与真实分布X构成的等高线垂直,即上图中的红色路径。蓝色是红线在某一点的切线,也就是梯度下降无噪音信号。蓝线的方向是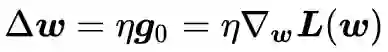
假如我们在蓝线的基础上加入垂直于 g0 的随机噪音,得到的有噪音梯度就可以看作是在一个圆锥的立体角范围内随机采样一个新的梯度 g 。上图中绿色圆锥比橙色拥有更大噪音,橙色采样梯度则比绿色采样梯度拥有更大的信号噪音比。
理论上只要保证足够大的训练集,使 BGD 计算出的梯度无限接近真实分布的梯度,并且让学习速率趋近于 0,就能保证下降路径基本上与红线重叠,收敛到最优解。然而真这样做的话,训练所需的时间怕是要等到天荒地老了,这时候我们可以妥协一部分信噪比,以换取每轮更快的计算速度,依靠更多轮迭代缩短训练所需的总时间。
然而,大多数人没意识到的是:添加的噪音,其作用不只是加快训练,更重要的是它也在帮助压缩向量 t 的信息 H(T),可以减小范化误差。
为了简化说明问题,这里暂时把 w 和 x 都看作 1 维,高维情况的原理是一样的。 t=wx ,也暂时省去非线性部分 relu,激活函数的确可以压缩 H(T),但机制与离散化并没有本质差别,与梯度噪音是不同的。
假设我们已有一个训练到一半的神经网络,下一次更新权重w时我们完全抛弃梯度信号,改用随机噪音 ζ 代替更新,来分析一下条件熵 H(X|T) 会怎样改变。以上标 ' 表示下一轮迭代时的值,不带上标的表示当前值。
噪音更新后目标层的 feature 值 t'=(w+ζ)x=t +ζx。
噪音与信号不相关,所以概率满足 p(x, t') = p(x, t)q(ζ)。
p 是数据的概率密度分布,q 是噪音的概率密度分布。同时概率密度 p 和 q 的积分都是 1。
(x, t) 与 ζ 相互独立,所以第一项很容易简化得到 H(X, T) + H(ζ)。
使用 Jensen 不等式改写第二项上的针对 ζ 的积分:
假设噪音的均值为 0,且正负分布对称(例如高斯噪音或白噪音),正负噪音对 t 的修正预期=0,那么迭代前后的 log(p(t)) 预期值应该是一样的。
因为概率密度不为负数,所以第二项存在下限:
所以:
我们看到使用噪音更新权重会导致 H(X|T) 增加,因为 H(X) 固定,所以 I(X, T)=H(X) - H(X|T) 必然减少。每一轮更新都参杂一些噪音进去,就能让 I(X, T) 缩小,同时信号使 I(Y, T) 扩大,但 I(Y, T) 的上限毕竟很低,所以 H(T) 在训练收敛阶段的变化,主要由 I(X, T) 决定,从而导致范化误差被不断降低。
上面的推导适用于 t'= t + f(ζ, ▽wL) 迭代更新的模型,相同输入 x 的情况下特征值 t(x) 的下一轮更新后的值,由噪音以及信号决定其更新量。所以理论上不只是神经网络,xgboost 这类的传统算法的迭代收敛过程也是相同的原理。
噪音的添加方法可谓是五花八门,下面随便列几条:
SGD的随机梯度,信噪比随着 batch size 的增加而增加;
drop out 的随机遮盖也对 t 值添加了噪音;
各种 tree 衍生的算法里的 column drop out 也是同样道理;
GAN 生成器的白噪音自带 I(T, X) 初始值基本为 0 的属性,所以不太担心范化误差的问题,只需要提升 I(T, Y) 即可;
VAE 的噪音则是源自于 normal distribution 中的采样。
总结
信息瓶颈理论的作者 Naftali Tishby 说过“学习的重要一步就是遗忘,对细节的遗忘使得系统能够形成通用的概念”。这句话非常准确地概括了目前大部分模型在迭代(学习)时正在进行的事情。仔细想想,人脑又何尝不是这样的呢?
所有监督学习,都绕不开三件事: 坐标转换,增加I(T, Y),以及减少I(T, X)。
每件事都要在训练过程的某一阶段被执行,才能保证利用有限的数据集学习到足够通用的结果。坐标转换确保可解释性,后面两件事负责平衡欠拟合和过拟合。
最后开个脑洞:人脑对于少样本训练的范化误差是远比机器学习模型的效果要好的,那么对于任何一个新概念 Y,其在各层抽象级的表述分别为,人脑必然有非常高效的
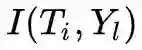
,最大程度利用已有的知识。同时对于同一抽象级的不同概念
,尽量让它们描述不同的信息,即减小
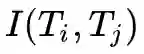
程序里评估互信息是一件非常麻烦的事情,所以目前机器学习的 loss 仍是基于 MC 采样估算 KL 距离和最小二乘的方法,如果能搞清楚人脑评估互信息的方式,或许人工智能的 loss 定制的问题就能很好得到解决,而这样的 loss 或许才是更贴近“知识”的本质的。
点击以下标题查看更多往期内容:

让你的论文被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢? 答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学习心得或技术干货。我们的目的只有一个,让知识真正流动起来。
📝 来稿标准:
• 稿件确系个人原创作品,来稿需注明作者个人信息(姓名+学校/工作单位+学历/职位+研究方向)
• 如果文章并非首发,请在投稿时提醒并附上所有已发布链接
• PaperWeekly 默认每篇文章都是首发,均会添加“原创”标志
📬 投稿邮箱:
• 投稿邮箱:hr@paperweekly.site
• 所有文章配图,请单独在附件中发送
• 请留下即时联系方式(微信或手机),以便我们在编辑发布时和作者沟通
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。
▽ 点击 | 阅读原文 | 获取最新论文推荐