【材料课堂】TEM复杂电子衍射花样的标定原理

会员服务 ·

【材料课堂】TEM复杂电子衍射花样的标定原理

2019 年 4 月 12 日 材料科学与工程

点击上方「材料科学与工程」快速关注

材料类综合、全面、专业的微信平台

1.1 超点阵花样

当晶体是由两种或者两种以上的原子或者离子构成时，对于晶体中的任何一种原子或者离子，如果它能够随机地占据点阵中的任何一个阵点，则我们称该晶体是无序的；如果晶体中不同的原子或者离子只能占据特定的阵点，则该晶体是有序的。

晶体从无序相向有序相转变以后，在产生有序的方向会出现平移周期的加倍，从而引起平移群的改变。由此引发的最显着的特点是在某些方向出现与平移对称对应的超点阵斑点。

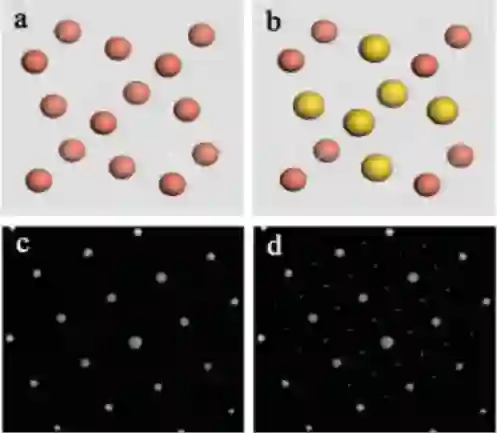
上图即是 CuAu3无序和有序的模型和对应的电子衍射花样。其中图 a 是 CuAu3无序时的晶体结构模型，而图 b 是有序时的晶体结构模型；图 c 是与无序对应的电子衍射花样，而图 d 则是与有序对应的超点阵电子衍射花样。

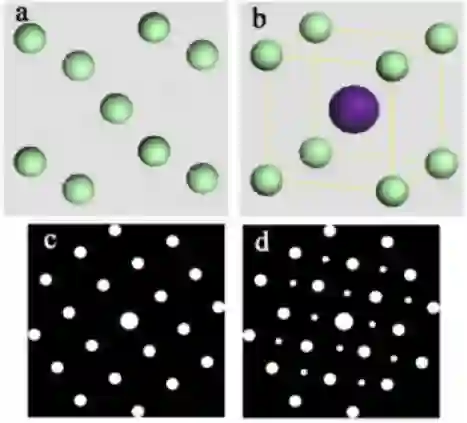
上图是 CsCl 无序和有序的模型和对应的电子衍射花样。其中图 a 是 CsCl 无序时的晶体结构模型，而图 b 是有序时的晶体结构模型；图 c 是与无序对应的电子衍射花样示意图，而图 d 则是与有序对应的超点阵电子衍射花样示意图。

上图是超点阵花样的一些实例，这些花样是从一种沿[111] 方向具有六倍周期的复杂有序钙钛矿相中得到的。图 a 是沿[010] 方向 2 倍周期有序的超点阵电子衍射花样，图 b 是沿[101] 方向 2 倍周期有序的超点阵电子衍射花样，图 c 是沿[11－1]方向 2 倍周期有序的超点阵电子衍射花样，而图 d 则是沿[111] 方向 6 倍周期有序的电子衍射花样。

1.2 高阶劳埃斑

以入射束与反射球的交点作为原点，构造出与晶体对应的倒易点阵。则对于正空间中的任一晶带轴，与之垂直而且过倒易空间的原点的倒易面，称之为该晶带的零层倒易面，该倒易面上的所有晶面与晶带轴之间满足晶带轴定律，通常我们得到的某晶带轴的电子衍射花样就是该晶带轴的零层倒易面。对于任一晶带轴而言，除了零层倒易面之外，所有与零层倒易面平行的倒易平面都与之垂直，但这些倒易面与晶带轴之间不满足晶带轴定律，它们之间的关系满足广义晶带轴定律，所有与零层倒易面平行的倒易平面统称为高层倒易面。

高层倒易面中的倒易阵点由于某些原因也有可能与倒易球相交而形成附加的电子衍射斑点，这就是高阶劳埃斑。

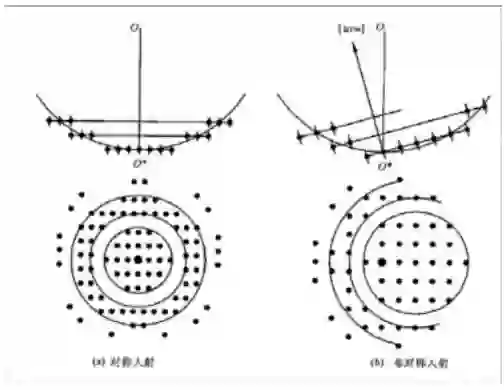
高阶劳埃带形成的示意图

劳埃斑产生的原因：

1.由于薄膜试样的形状效应，使倒易阵点变长，这种伸长的倒易杆增加了高层倒易面上倒易点与反射球相交的机会；

2.晶格常数很大的晶体，其倒易阵点排列更密，倒易面间距更小，使得上下两层倒易面与零层倒易面同时与反射球相交的机会增加；

3.当电子衍射花样不正，使得零层倒易面倾斜时，增加了高层倒易阵点与反射球的相交机会；

4.电子波的波长越长，则反射球的半径会越小，这样也会增加高层倒易面上的倒易点与反射球相交后仍然能在底片处成像的机会。

高阶劳埃带衍射花样实例

1.3 孪晶电子衍射花样

所谓孪晶，通常指按一定取向关系并排生长在一起的同一物质的两个晶粒。从晶体学上讲，可以把孪晶晶体的一部分看成另一部分以某一低指数晶面为对称面的镜像；或以某一低指数晶向为旋转轴旋转一定的角度。

孪晶的分类：

1、按晶体学特点：反映孪晶和旋转孪晶；

2、按形成方式：生长孪晶和形变孪晶；

3、按孪晶形态：二次孪晶和高次孪晶。

上图中图 a 和 b 是 CaMgSi相中的（102）孪晶在不同位向下的孪晶花样，图 c 是 CaMgSi相中另外一种孪晶的电子衍射花样，其孪晶面是 (011)面；图 d 是镁中常见的（10－12）孪晶花样。

上图是 CaMgSi相中（102）孪晶中二重孪晶和三重孪晶的形貌和与其对应的电子衍射花样。图 a 是二重孪晶的形貌（暗场像），图 b 是与之对应的二重孪晶花样；图 c 是三重孪晶的形貌像（暗场），图 d 是与之对应的三重孪晶花样。

1.4 二次衍射

在电子束穿行晶体的过程中，会产生较强的衍射束，它又可以作为入射束，在晶体中产生再次衍射，称为二次衍射。二次衍射形成的新的附加斑点称作二次衍射斑。二次衍射很强时，还可以再行衍射，产生多次衍射。

产生二次衍射的条件：

1、晶体足够厚；

2、衍射束要有足够的强度。

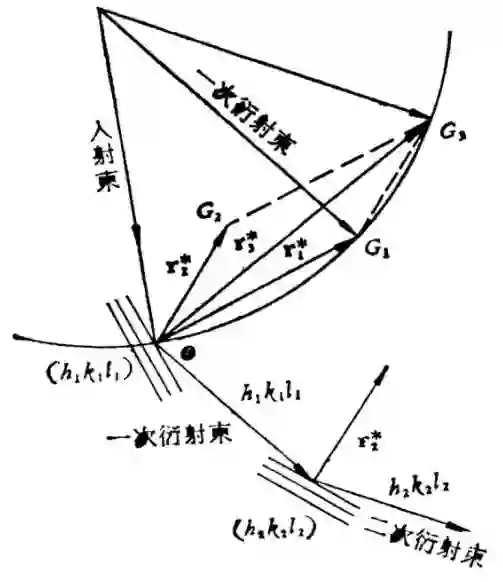
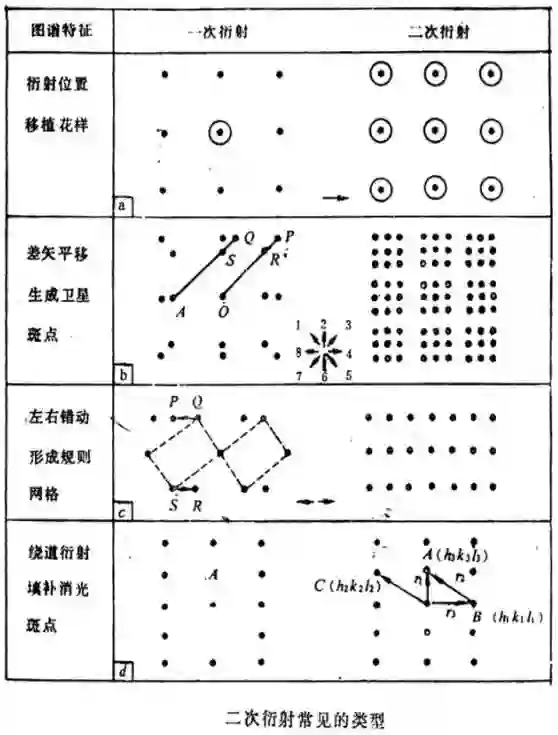
二次衍射花样形成的示意图

二次衍射花样实例

上图是二次衍射中出现多余衍射斑点的两种不同，其中图 a 是在镁钙合金中得到的的电子衍射花样，图中本来只存在两套花样，分别是镁的[-1100] 晶带轴电子衍射花样和 Mg2Ca相的[3-302] 晶带轴花样。而花样中出现的很多卫星斑是由于二次衍射，通过 Mg2Ca相的(1-103) 斑点与 Mg的(000-2) 斑点之间存在的差矢平移造成的。图 b 和图 c 是一种有序钙钛矿相中沿[010]p 方向得到的电子衍射花样，其中图 b 是在较厚的地方得到，而图 c 则是在很薄的地方得到。在较薄的地方，由于不存在动力学效应，可以清楚地看到花样中存在相当多消光的斑点，但在较厚的地方，由于动力学效应，出现二次衍射的矢量平移，使得本来应该消光的斑点变得看起来不消光了。

1.5 菊池花样

在稍厚的薄膜试样中观察电子衍射时，经常会发现在衍射谱的背景衬度上分布着黑白成对的线条。这时，如果旋转试样，衍射斑的亮度虽然会有所变化，但它们的位置基本上不会改变。但是，上述成对的线条却会随样品的转动迅速移动。这样的衍射线条称为菊池线，带有菊池线的衍射花样称之为菊池衍射谱。

菊池花样在晶体材料分析方面，广泛用于物相鉴定、衬度分析、电子束波长以及临界电压的测定等。它更重要的一个应用是用来精确测定晶体取向，用菊池线来测定晶体的取向时，其精度可以达到 0.01°, 是精确测定晶体取向、位向关系和迹线分析的理想方法。

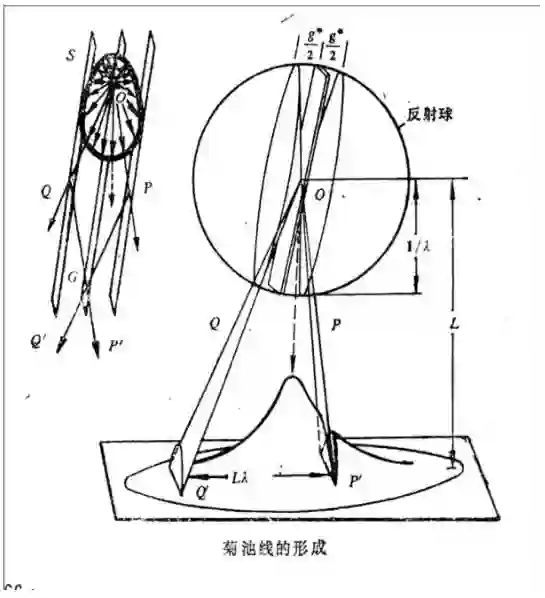
菊池线的形成示意图一

电子束在穿透较厚的试样时，入射电子与试样之间会发生相互作用，其中有部分电子会发生非弹性散射。但是非弹性散射之后，它们的能量损失也只有几十电子伏特，相对透射电镜几十万伏的加速电压来说，这个能量是非常小的，因此可以认为非弹性散射以后，电子波的波长基本没有变化。因此当这一部分电子波在满足布拉格条件产生衍射时，其几何关系与弹性散射电子可以认为没有差别。

非弹性散射电子进入晶体以后，向各个方向散射的几率并不相等，沿透射束方向的散射几率最大，随散射角增大，其散射的几率减小，非弹性散射引起的强度相应地会逐渐降低，这样就形成了衍射照片上中间亮四周渐暗的衍射谱背景（这个背景是由非弹性散射电子形成的，如示意图一所示）。

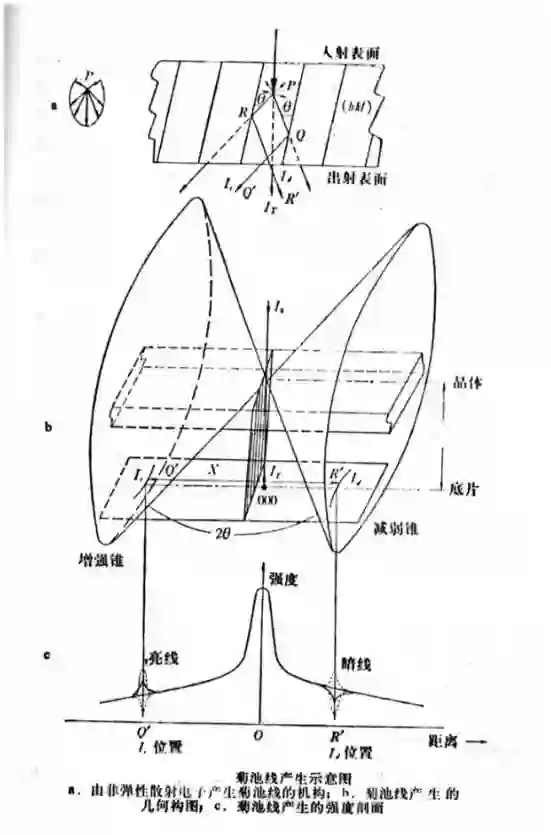
菊池线的形成示意图二

菊池线的形成原理

非弹性散射的电子不与晶体相互作用产生衍射时，在背底上将不会出现明显的衬度，但当非弹性散射电子与某一晶面产生衍射时，会在某些方向产生衬度。如示意图二所示，当 hkl 面不平行于入射束方向时，从 P点射出的散射线 PQ如果满足衍射条件，则其反射线 QQ’也会满足衍射条件，即 PR也满足衍射条件。但是对于非弹性散射束而言， PQ 方向的强度要大于 PR方向的强度，所以产生衍射后， PQ方向的强度为 PQ+RR ’－QQ’，而PR方向的强度为 PR+QQ ’－RR’。最终的结果，使得 PQ方向强度有所降低，这相当于在“山峰附近留下一条暗沟”，形成暗线；而 PR方向的强度有所增加，这相当于在“山谷处形成一道矮墙”，形成亮线。

对于 hkl 晶面来说，所有可能的衍射方向构成一个半顶角为 90°－θ 的衍射圆锥，这些射线锥和距离晶体较远而又垂直于入射束的底片相截于两支抛物线，由于 θ 值很小，这两支抛物线非常接近于直线，因此在底片上得到的成对的菊池线看上去是两条直线。

菊池衍射谱的特点

1.hkl 菊池线对与中心斑点到 hkl 衍射斑点的连线正交，而菊池线对的间距与两个斑点之间的距离也相等；

2.菊池线一般是明暗配对的直线，在正片上距离透射斑近者为暗线，远者为亮线；

3.菊池线对的中心线则相当于反射晶面与底片的交线；两条中心线的交点即为两个对应平面所属的晶带轴与荧光屏的截点，一般称之为菊池极；

4.当晶体取向改变不大时，衍射斑点基本不移动，但强度会有所变化，但是菊池线对取向非常敏感，当晶体稍微转动时，它会发生非常明显的移动；

5.当出现多个菊池极时，实际上已经带出了晶体的三维信息，这个时候就不会有 180°不唯一性。

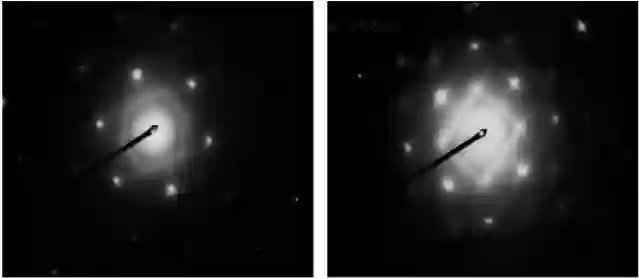
菊池衍射谱实例

菊池图实例

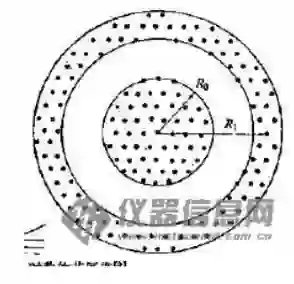
1.6 非晶的衍射花样

1. {Chen, 2004 #2} 衍射斑点规则排列单晶

2. 衍射斑点散乱多晶

3. 衍射斑点散乱但是隐约能看到环状的轮廓多晶，晶粒很多

4. 锐利的衍射环宽化的环，是非晶

5. 弥散的多个衍射环多个宽化的环，非晶

6. 弥散的一个衍射环一个宽化的环，可能是非晶，但这么不清楚，有时候试样太厚也会出现这种情况

7. 大衍射斑点中间又有小衍射斑点 Ag 的[111] 面，很有名的超晶格

8. 有序金属间化合物经常会有弱点出现。此图还不能说是超晶格，只能算是孪位错

9. 衍射斑点规则排列的周围多了一个环，环上是由多个规则排列的衍射斑点组成。这个比较难找到照片，就用郭先生的书里的示意图贴上来吧

这个就是孪晶的电子衍射，有明显的衍射点分裂现象。

通用单晶电子衍射花样的标定步骤

测量衍射花样上透射斑到衍射斑的三个最短距离 R1、R2、R3 及其之间的夹角：

根据公式， d = R/ （L×电子波长），其中 L 是相机常数，底片上写着，单位是 cm，电子波长一般的电镜书上都有，200 kV 电镜是 0.00251 nm。代入计算即可得到相应的 d 值。计算对应的三个面间距值 d1,、d2和 d3，与 JCPDF卡片相比较，找出相吻合的晶面族指数{h1k1l1} 、{h2k2l2} 和{h3k3l3};

在{h1k1l1} 中任选(h1k1l1) 为 A点指数，然后从{h2k2l2} 中试探确定 B点指数(h2k2l2) ，并使得 h3=h1+h2 ， k3=k1+k2，l3=l1+l2 ；

计算面夹角，与测量值比较，如果计算值与测量值相符则标定正确；? 根据右手螺旋法则计算晶带轴指数。

验证标定的正确性

确定 h1k1l1、h2k2l2 和 h3k3l3 后还需要用晶面间的夹角验证标定的正确性。例如，在底片上测得 h2k2l2 和 h3k3l3 之间的夹角 α 为 31.5 度，理论计算（011）和（111）之间的夹角为 31.4 度，理论计算值与实验测量值基本符合，说明标定是正确的。

备注：一般晶面之间的夹角理论计算值与实验测量值的误差在 0.5 度之内认为标定是正确的，而且最好将两个角度（ h1k1l1 ^ h3k3l3 ， h2k2l2 ^ h3k3l3 之间的角度）都验证一下。如果误差超过 0.5 度，那么就需要重新仔细测量实验夹角或重新确定 h1k1l1 、h2k2l2和 h3k3l3。（来源：仪器信息网）