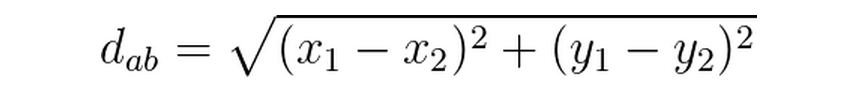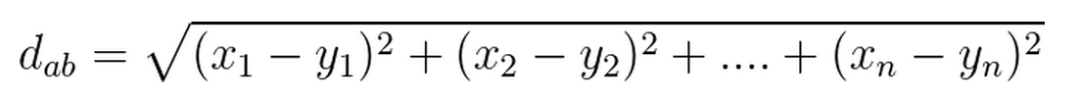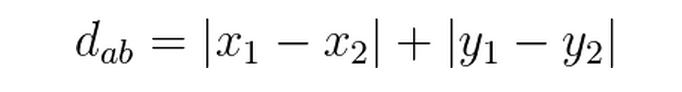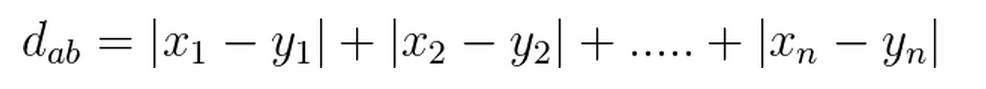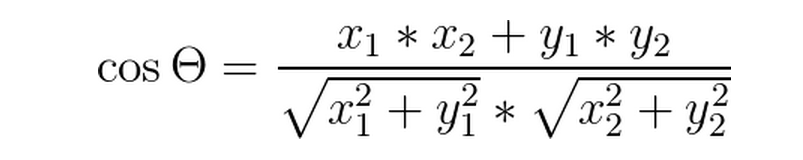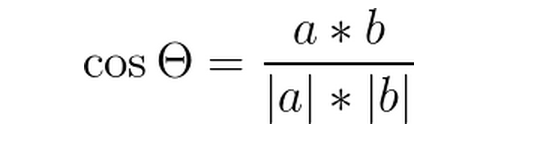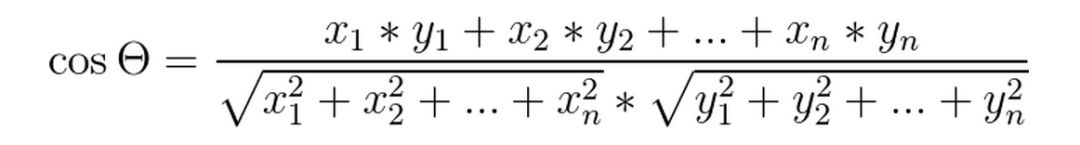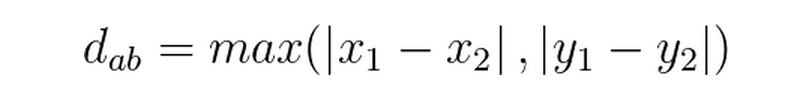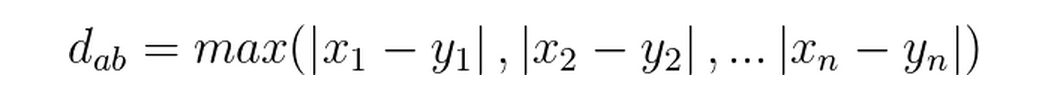机器学习的5种距离度量方法

在机器学习领域中有非常多的问题需要求距离，常见的是向量距离的计算。比如判断A、B、C三种商品之间的相似性，可以先按照商品特征构建A、B、C的各自的向量，然后求向量间的距离，距离近就表示彼此相似度高。今天讲下常见的几种距离计算方法。

A 欧式距离EuclideanDistance

欧式距离：两点之间的直线距离。

(1)二维平面上两点a(x1,y1)，b(x2,y2)之间的欧式距离公式：

(2) n维空间上两点a(x1,x2……..xn)，b(y1,y2……..yn)的欧式距离公式：

B  曼哈顿距离(ManhattanDistance)

曼哈顿距离也叫”曼哈顿街区距离”。想象你在曼哈顿街道上，从一个十字路口开车到另一个十字路口，驾驶距离就是这个“曼哈顿距离”。

(1)二维平面上两点a(x1,y1)，b(x2,y2)之间的曼哈顿距离公式：

(2) n维空间上两点a(x1,x2……..xn)，b(y1,y2……..yn)的曼哈顿距离公式：

C 夹角余弦

机器学习中可以把两点看成是空间中的两个向量，通过衡量两向量之间的相似性来衡量样本之间的相似性。

(1)二维平面上两向量a(x1,y1)，b(x2,y2)之间的夹角余弦公式：

也可直接通过向量运算：

(2) n维空间上两点a(x1,x2……..xn)，b(y1,y2……..yn)的夹角余弦公式：

D 切比雪夫距离（Chebyshevdistance）

切比雪夫距离:各对应坐标数值差的最大值。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？你会发现最少步数总是max( | x2-x1 | , | y2-y1 | )步。

(1)二维平面上两点a(x1,y1)，b(x2,y2)之间的切比雪夫距离公式：

(2) n维空间上两点a(x1,x2……..xn)，b(y1,y2……..yn)的切比雪夫距离公式：

E 汉明距离

两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。

1011101与 1001001 之间的汉明距离是2  　

2143896与 2233796 之间的汉明距离是3  　

irie与 rise之间的汉明距离是 3

《机器学习集训营 第四期》九城同步开营，周日第一节线下课，10个工业项目实战辅导 + 一对一面试求职辅导，剩余5个线下试听名额，有意者请速加微信客服：julyedukefu01