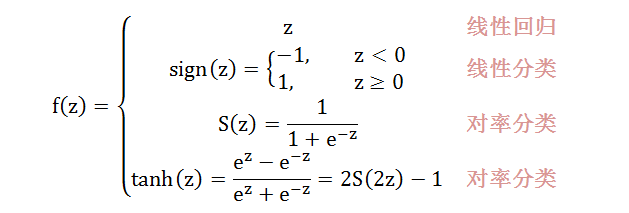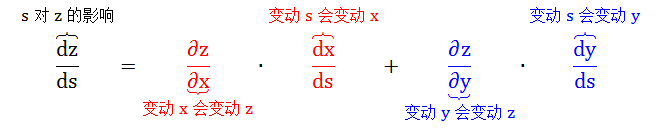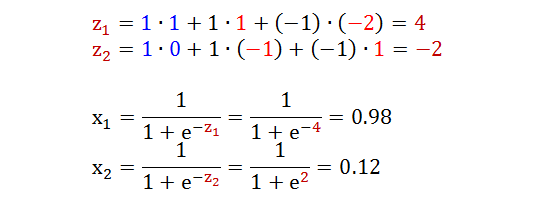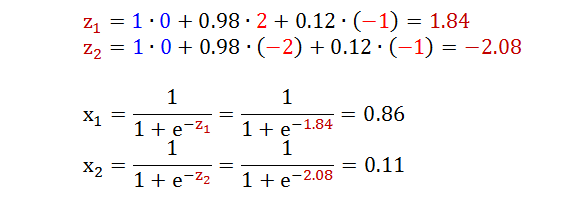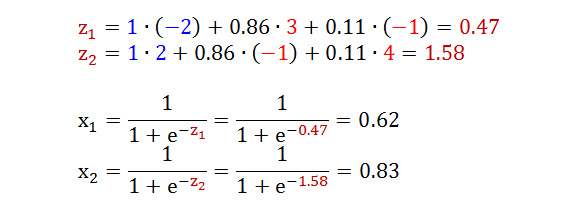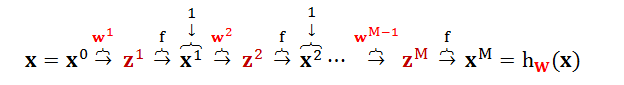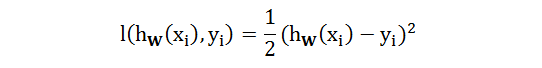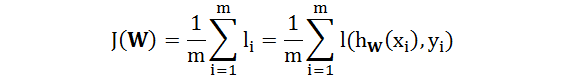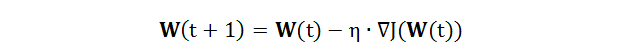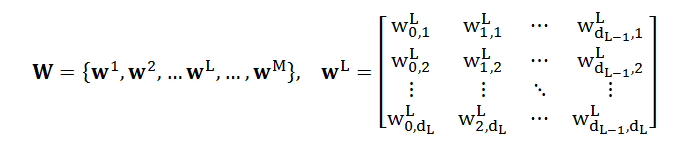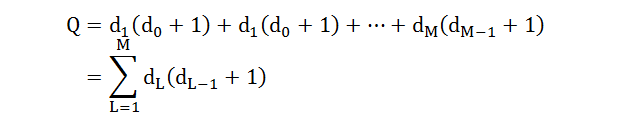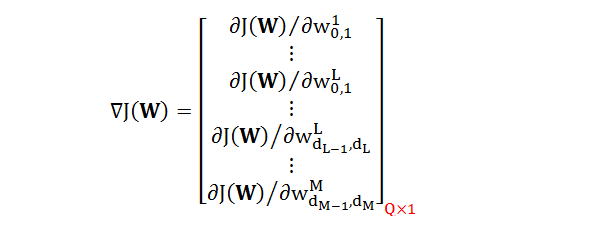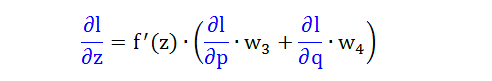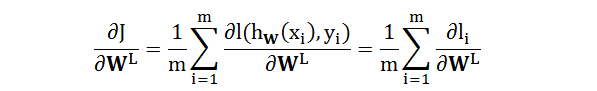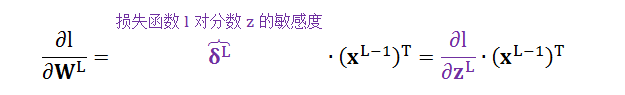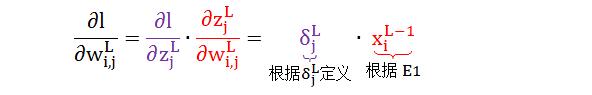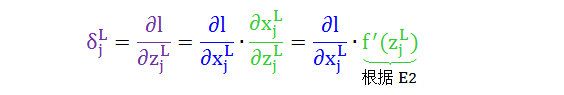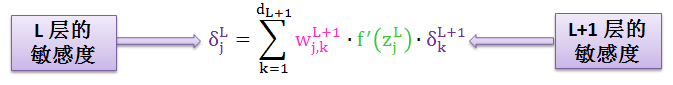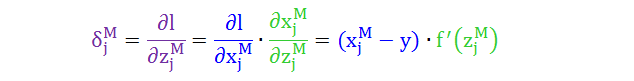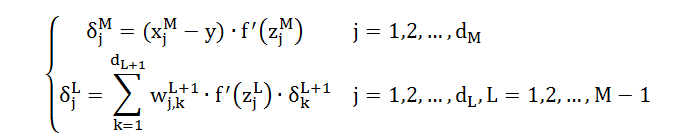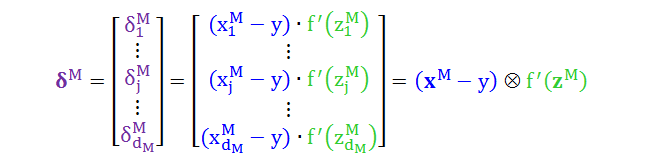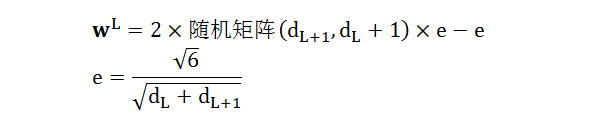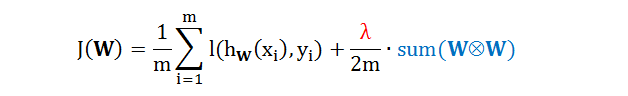人工神经网络之正反向传播

引言

考你一道非常简单的题，给定表达式 

    e = (a+b) × (b+1)

并给定一组 a 和 b 值，比如 a = 2, b = 1，计算

1. e 的值

2. e 对 a, b 的变化率 (也就是 a, b 变化 1 个单位，求出 e 变化多少个单位)

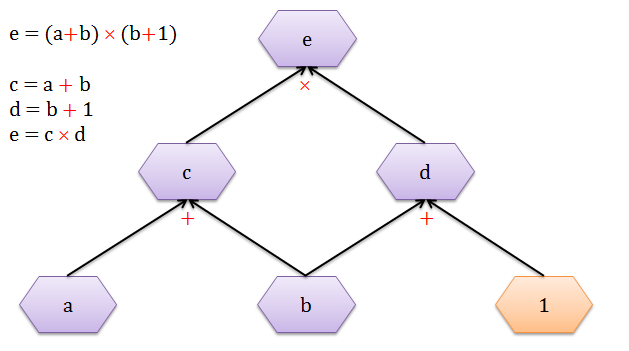
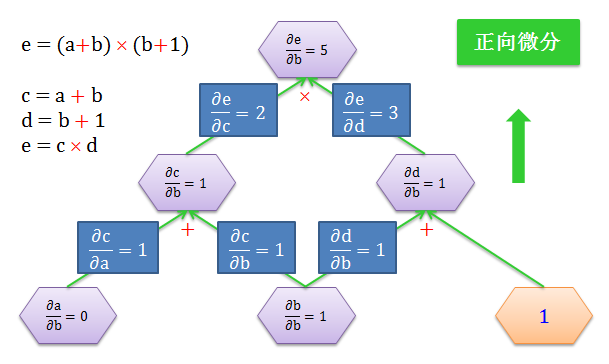
用 c = a + b，d = b + 1 的代换，画出下面的计算图 (computational graph)。图中有三个运算符：2 个加法 (+) 和 1 个乘法 (×)。紫色六边形里面的是变量，橙色六边形里面是常数。

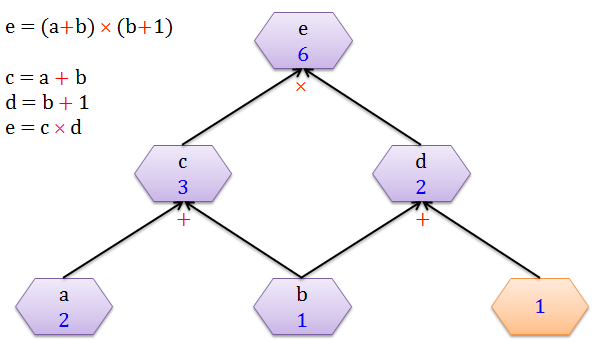
当 a = 2, b = 1 时，从下往上 (黑色箭头) 的计算出 c = 3, d = 2 以及 e = 6。整个过程就是正向传播 (forward propagation)，顾名思义就是沿着正方向做一些计算。

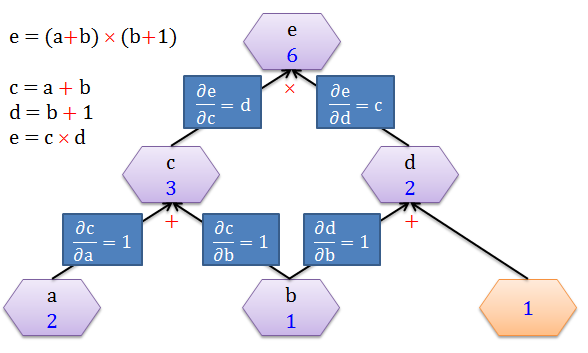
接下来要计算 e 对 a, b, c, d 的变化率，首先来看看在每条边 (edge) 的导数 (derivative)，如下图：

因为 c = a + b

 

• 当 a 变化 1 个单位，c 变化 1 个单位，∂c/∂a = 1/1 = 1

• 当 b 变化 1 个单位，c 变化 1 个单位，∂c/∂b = 1/1 = 1

因为 d = b + 1

• 当 b 变化 1 个单位，d 变化 1 个单位，∂d/∂b = 1/1 = 1
  

因为 e = c × d

• 当 c 变化 1 个单位，e 变化 d 个单位，∂e/∂c = d/1 = d

• 当 d 变化 1 个单位，e 变化 c 个单位，∂e/∂d = c/1 = c

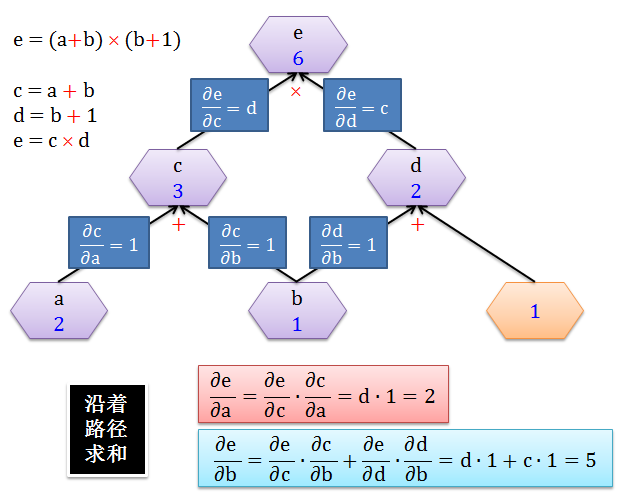
有了每条边上的导数，计算 e 对于 a 或 b 的变化率就是加总所有经过 a 或 b 的路径 (sum over path)，如下图所示：

很显然

• ∂e/∂a 只有一条路径，可以理解当 a 变化 1 个单位，则 c 变化 1 个单位，则 e 变化 2 个单位，因此 ∂e/∂a = ∂e/∂c × ∂c/∂a = 2

  
  

• ∂e/∂b 只有两条路径，可以理解当 b 变化 1 个单位
  

  
  

• c 变化 1 个单位，则 e 变化 2 个单位

• d 变化 1 个单位，则 e 变化 3 个单位

  
  

因此 ∂e/∂b = ∂e/∂c × ∂c/∂b + ∂e/∂d × ∂d/∂b = 2 + 3 = 5

在计算变化率问题上，有两种类型：

1. 从 b 开始正向往上计算所有节点上的变量对 b 的导数，该操作叫做正向微分 (forward-mode differentiation)

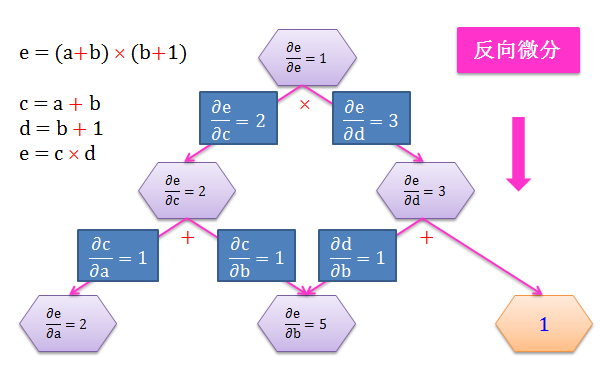
2. 从 e 开始反向往下计算 e 对所有节点上的变量的导数，该操作叫做反向微分 (backward-mode differentiation)

如下面两图所示：

在该问题中，e 是输出：

• 做一次正向微分只能得到 e 对一个输入 (比如 b) 的变化率

• 做一次反向微分却能得到 e 对所有输入 (a, b, c, d) 的变化率

在神经网络 (artificial neural network, ANN) 里面，把 e 当成代价函数，a, b, c, d 当成权重，在梯度下降求权重最优解时就需要代价函数对所有权重的偏导数 (变化率的极限说法)。那么明显反向微分是我们需要计算偏导数的方式。而反向微分这个过程在 ANN 里面的术语称为反向传播 (backward propagation, backprogapation)，顾名思义就是沿着反方向做一些计算。

第一章以极度细微的方式介绍构成 ANN 的基本元素，比如层、节点、箭头、转换函数、权重和分数，并写出 ANN 漂亮的代数和矩阵表达形式；第二章主讲正向传播和反向传播，数学符号非常繁重，但是每小节都有一个简单例子入手帮助理解后面严谨的数学推导；第三章用 Matlab 代码实现一个简单的识别手写数字的 ANN。

目录

第一章 - 前戏王

    1.1 层

    1.2 节点

    1.3 箭头

    1.4 转换函数

    1.5 权重和分数

    1.6 数学表达形式

    1.7 矩阵表达形式

    1.8 链式法则

第二章 - 理论皇

    2.1 正向传播

    2.2 梯度下降

    2.3 反向传播

第三章 - 实践狼

    3.1 问题描述

    3.2 数据解析

    3.3 正向传播

    3.4 反向传播

    3.5 梯度检验

    3.6 其他技巧

总结

第一章 - 前戏王

本节目的是弄清神经网络的里面每个概念和了解其运作，为了达到此目的，我们必须介绍一套系统的数学符号。咋一看可能会头晕目眩，但是相信我一定能给你讲明白，花点时间捋清它们是绝对值得的。

首先以极简的方式来概括神经网络，

• 神经网络是分层 (layer) 的

• 每层上是有节点 (node) 的

• 节点和节点之间是由箭头 (arrow) 连接的

• 节点上有转换函数 (transfer function) 的

• 箭头是承载着权重 (weight) 的

之后从最初输出开始，权重乘以输出加工成分数，分数通过转换函数生成输出，一层一层，生生不息，直到最后。。。

1.1

层

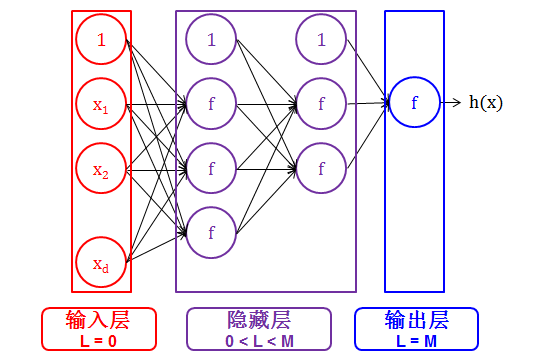
神经网络是分层 (layer) 的。

神经网络的每层用 L 表示，其中 L = 0, 1, 2, …, M.

 

• 输入层 (input layer) 严格来说不被认为是层，因此用 0 层表示

• 输出层 (output layer) 决定神经网络的最终输出

• 隐藏层 (hidden layer) 夹在输入层和输出层的中间

1.2

节点

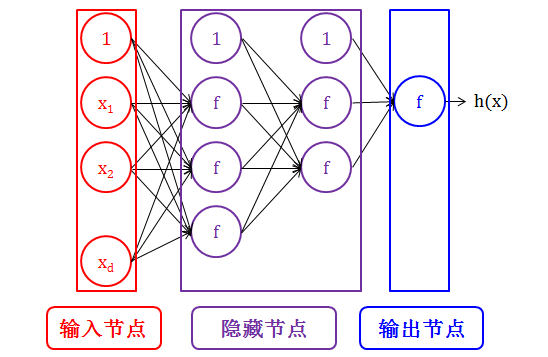
神经网络的每层上是有节点 (node) 的。节点的划分有两种方式：

节点由层的类型划分：

• 在输入层上的节点叫做输入节点 (input node)

• 在输出层上的节点叫做输出节点 (output node)

• 在隐藏层上的节点叫做隐藏节点 (hidden node)

节点由连接箭头 (connecting arrow) 的类型划分：

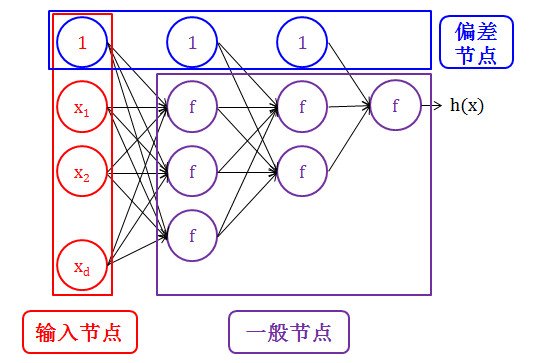
• 除输出层的每一层都有一个特殊的节点叫做偏差节点 (bias node)，该节点没有输入箭头 (incoming arrow) 只有输出箭头 (outgoing arrows)

• 输入节点 (input node) 没有输入箭头，只有输出箭头

• 一般节点 (normal node) 既有输入箭头，也有输出箭头

1.3

箭头

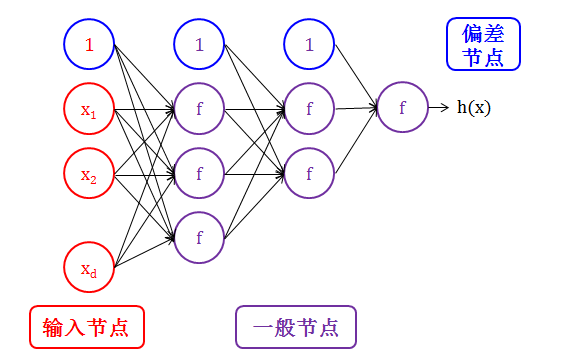
节点和节点之间是由箭头 (arrow) 连接的。

除了在输出层，每个箭头连接着上一层的节点和下一层的节点：

• 偏差节点和输入节点没有输入箭头，只有输出箭头

•  一般节点既有输入箭头，也有输出箭头

1.4

转换函数

在神经网络世界里，节点与节点之间是靠转换函数 (transfer function) 连接的，而转换函数就是一种将输入 (input) 转成输出 (output) 的函数，如下图所示：

神经网络用的最多的转换函数，分别是

1.5

权重和分数

箭头是承载着权重 (weight) 的，从上一层的输出开始，权重乘以输出加工成下一层的分数 (score)。

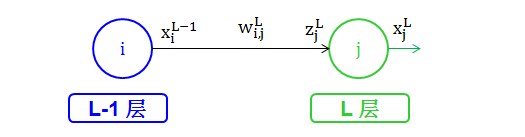
在第 L 层上，一般节点都是接受一个信号 z，又称为分数 (score) ，并发出一个信号 x

 

• 权重 wL 的上标为L，表示这它从上一层 (L-1层) 来，并走向下一层 (L 层)

• L-1 层的输出信号 xL-1 乘以权重 wL 得到分数 zL

  
  

• wLi,j 是权重，来自 L-1 层的节点 i，去向 L 层的节点 j

• zLj  是分数，也是 L 层的节点 j 的输入信号

• xLj 是 L 层的节点 j 的输出信号

1.6

数学表达形式

从 L-1 层到 L 层，给出以下数学符号定义：

• L-1 层有 dL-1+1 个节点，标注为 0,1,…,dL-1

• L 层有 dL+1 个节点，标注为 0,1,…,dL

• 偏差节点标注为 0

三种情况值得讨论：

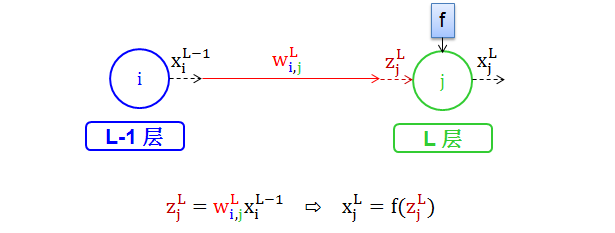
情况 1：一节点对一节点

其中

• 红色 wL 代表权重

• 蓝色下标 i 代表是权重来自第 L-1 层的节点 i

• 绿色下标 j 代表是权重走向第 L 层的节点 j

• 褐色 zLj  代表分数

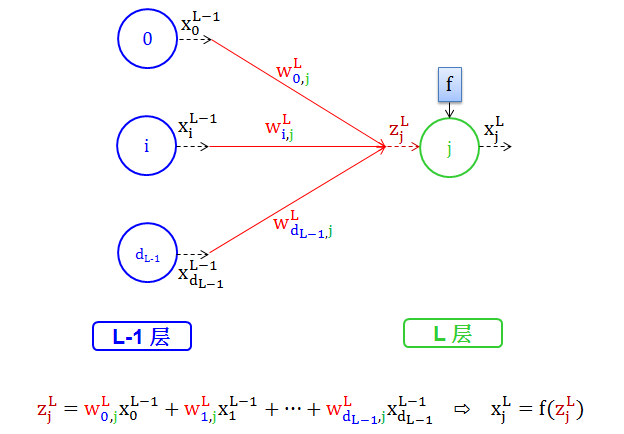
情况 2：多节点对一节点

其中

• 红色 wL 代表权重

• 蓝色下标 0,1,…,dL-1 代表是权重来自第 L-1 层的节点 0,1,…,dL-1

• 绿色下标 j 代表是权重走向第 L 层的节点 j

• 褐色 zLj  代表分数

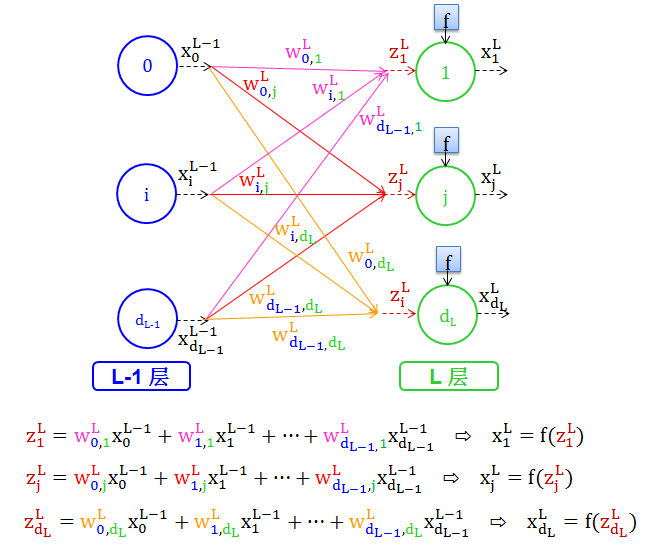
情况 3：多节点对多节点

其中

• 红色 wL 代表权重

• 蓝色下标 0,1,…,dL-1 代表是权重来自第 L-1 层的节点 0,1,…,dL-1

• 绿色下标1,2,…,dL 代表是权重走向第 L 层的节点 1,2,…,dL

• 褐色 zLj  代表分数

1.7

矩阵表达形式

能将情况 3 的数学表达式写成矩阵形式是未来弄懂整个神经网络正向后向算法的关键。定义列向量 zL 和 xL-1，矩阵 wL

其中

• xL-1 是 dL-1+1 的列向量

• wL 是 dL ∙ (dL-1+1) 的矩阵

• zL 是 dL 的列向量

• xL 是 dL+1 的列向量

我们可以轻而易举的把情况 3 里面的数学操作用矩阵来表示：

根据上面三步操作，我们已经得到了一轮从 L-1 层到 L 层的完整运算，即

1. 权重 wL 乘以 L-1 层输出 xL-1 加工成分数 zL 作为 L 层输入

2. 分数 zL 通过转换函数生成 f (zL)

3. 对 f(zL) 加入偏差项后整合成 L 层输出 xL

1.8

链式法则

情况一：y = f(x), z = g(y)，计算变动 x 对 z 的影响。

很明显变动 x 会变动 y，而变动 y 会变动 z，因此

情况二：x = f(s), y = g(s), z = h(x, y)，计算变动 s 对 z 的影响。

很明显变动 s 会变动 x 和 y，而变动 x 和 y 会变动 z，因此

第二章 - 理论皇

由于传播算法的推导需要繁重的数学符号和繁琐的微分迭代，因此在给出“复杂推导”之前，我会给出一个“简单示例”，目的就是为了让大家能抓住核心，因此数学符号可能用的不是那么严谨，无懈可击的数学符号留给“复杂推导”。

2.1

正向传播

正向传播 (forward propagation) 就是已知所有的权重和所有的转换函数，输入一组值，一层一层向前推进，最后输出一组值。

 

简单示例

 

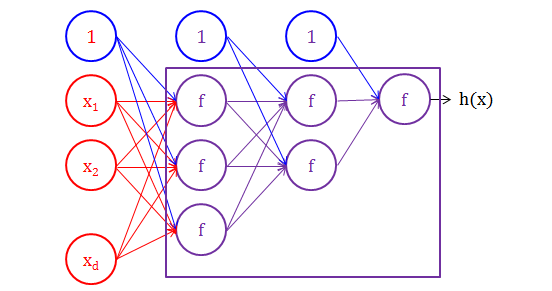
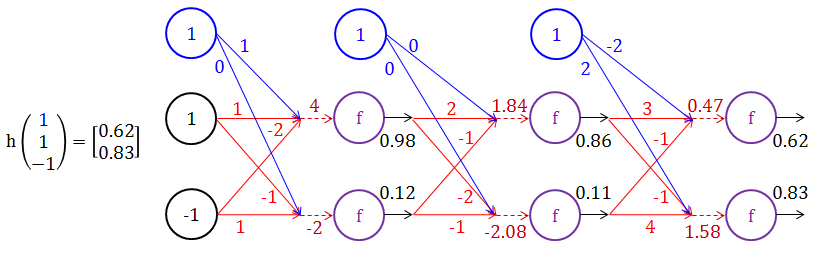
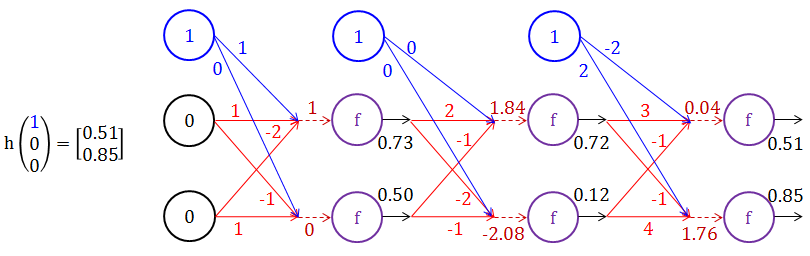
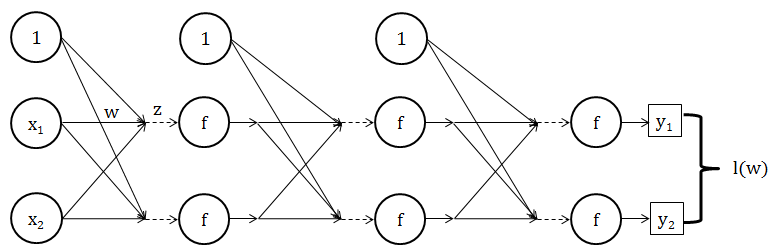
当输入为 [1 1 -1] 时，其中蓝色的 1 是偏差项，以下神经网络详细展示了如何从最初输入到最终输出。(蓝色代表偏差 x0 和其对应的权重 w0,j，红色代表权重 wi,j，褐色代表分数 z，假设转换函数 f 是 1/(1+e-s))

从输入层到第 1 层的运算如下：

从第 1 层到第 2 层的运算如下：

从第 2 层到第 3 层的运算如下：

再试试当输入为 [1 0 0] 时的计算流程?

由上可知，你就可以把整个神经网络看成是一个函数 h (它可能非常复杂)，而权重 W 就是这个函数 h 的参数。整个正向传播就是在计算 y = hW(x)，给定 100 个 x，正向传播就能算出100 个 y。

复杂推导

讲完简单例子后，我们就需要用严谨的数学符号来描述整个正向传播的流程，将一系列线性方程用矩阵形式表示，这对以后写代码都是有好处的。

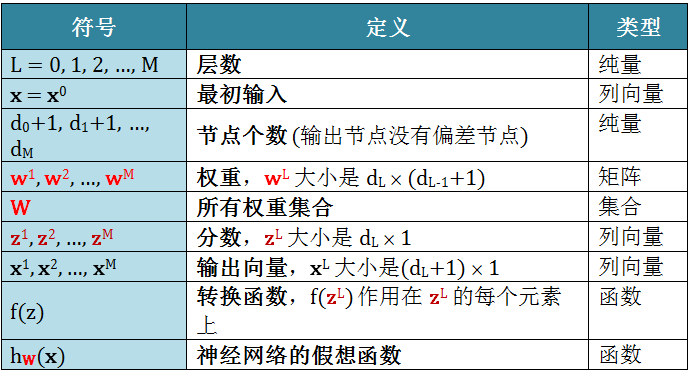
首先明确算法里需要用到的符号

定义完符号之后有没有想放弃？这么多的大小不一的矩阵和向量是如何连在一起的？继续看之前建议再看一遍小节2.7!

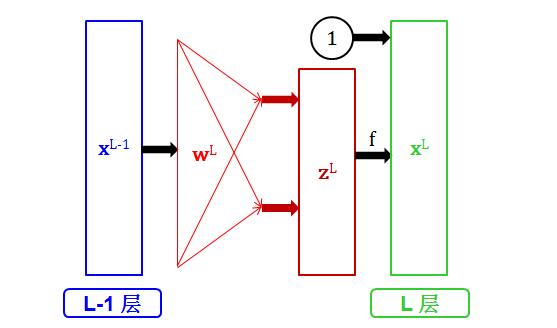
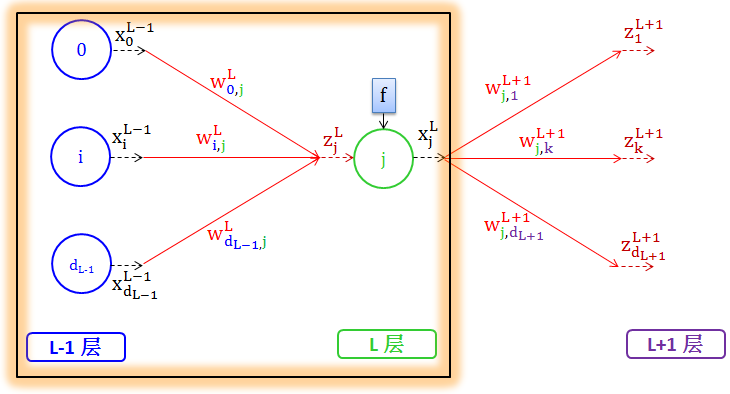
一开始写出每层的运算太麻烦，我们先把注意力放在从 L-1 层到 L 层正向传播算法，其流程图如下:

该流程图表达的意思是：

1. 权重 wL 乘以 L-1 层输出 xL-1 加工成分数 zL 作为 L 层输入

2. 分数 zL 通过转换函数生成 f (zL)

3. 对 f(zL) 加入偏差项 1 后整合成 L 层输出 xL

弄懂 L-1 层到 L 层正向传播算法之后，将 L 从 1 列举到 M 会不会？当然第 0 层就是输入层，需要做初始化；第 M 层就是输出层，是我们想要的最终结果。正向传播的算法如下：

整个正向传播的链式流程图如下:

           

现在你可以说，给我一组输入 x，给我全套权重 W，我就能算出一组输出 hW(x)。这种正向计算非常简单，只要你能摸清算法的流程，你就可以一气呵成的计算到底。你可以把 ANN 当成是个计算器或者函数 (它有自己的一套参数，即权重)，喂给它一组输入，它吐出一组输出。

2.2

梯度下降

上节用 ANN 的正向传播的计算很简单，可是实际问题只会让我们做出这样的一个正向计算么？细心的同学会说权重怎么得到？

这些同学考虑的问题很实际，实际问题就是

1. 计算出一组输出 hW(x)

2. 获取一组实际标识 y

3. 调节全套权重 W 来最小化两者的差异

给定一个样例 (xi, yi)，第 1 步用正向传播的方法得到  hW(xi) 的一个关于 W 的表达式，第 2 步直接获取 yi，第 3 步最小化  hW(xi) 和 yi 差异需要选择一个损失函数 l，以平方差类型为例定义如下：

代价函数 J 则是所有样例损失函数的加总：

在机器学习里，最小化代价函数 J 求得最佳权重 W 的数值方法都是梯度下降 (gradient descent)，算法如下：

其中 η 是学习率，∇J 是 J 对 W 的梯度。

在计算 J(W) 的梯度之前，我们先看看 W 里面到底有多少个参数

根据每个 wL 的大小是 dL ∙ (dL-1+1)，因此 W 的参数个数 Q 是

将 ∇J(W) 的每项写出来，是一个巨大的列向量，上百万个参数很常见：

用有限差分 (finite difference) 可以计算出梯度向量里面每项偏导数，但是要花费 O(Q2)，效率奇低，这时大名鼎鼎的反向传播算法 (花费只需 O(Q)) 终于要登场了。

2.3

反向传播

正向传播是按神经网络正方向走，计算每层对应的分数 z 和输出 x；与之对应的反向传播 (backpropagation) 是按神经网络反方向走，计算每层对应的偏导数 ∂J/∂W。

简单示例

 

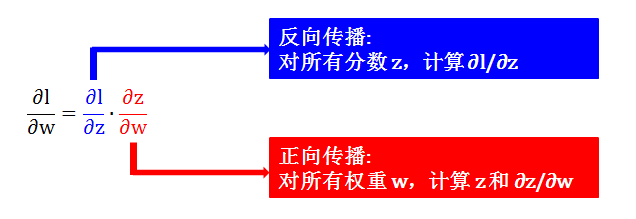
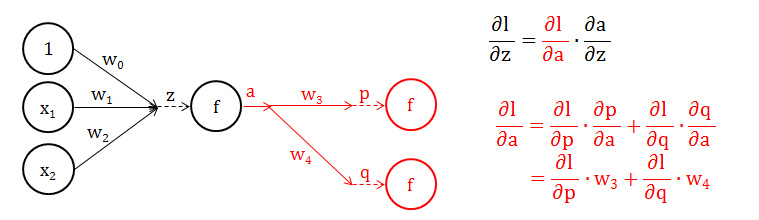
还是用正向传播里面那个简单的神经网络，假设最后损失函数是 l，我们来计算 l 对某一个权重 w 的偏导数 ∂l/∂w。

根据链式法则情况 1 (见小节1.8)，∂l/∂w 可以拆分成 ∂z/∂w 和 ∂l/∂z：

 

1. ∂z/∂w 可用正向传播计算出，因为分数 z 可被算出

2. ∂l/∂z 则需要反向传播计算

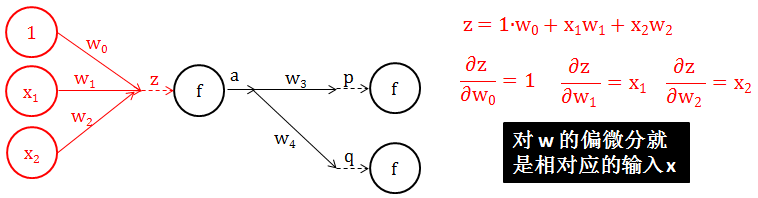
第 1 步：计算 ∂z/∂w (注意力放在下图红色部分)

 

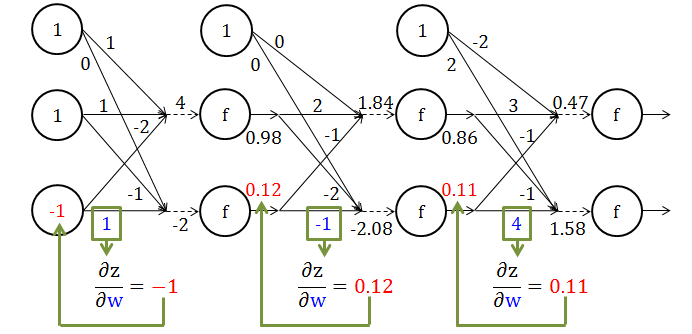
显然 z 是 w 的一个线性组合，其系数就是相对应的 x，那么 ∂z/∂w = x。下图给出一个具体计算 ∂z/∂w 例子。

 

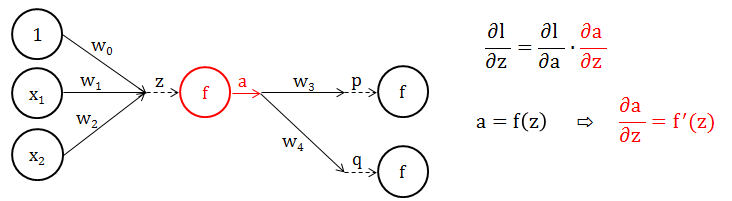
第 2 步：计算  ∂l/∂z，又根据链式法则情况 1 (见小节1.8)，∂l/∂z 可以拆分成 ∂l/∂a 和 ∂a/∂z。

 

第 2.1 步：首先解决简单的 ∂a/∂z (注意力放在下图红色部分) 

a 是什么？a 不就是分数 z 经过转换函数 f 加工出来的输出吗？因此 a = f(z)，那么 ∂a/∂z  = f’(z)

 

第 2.2 步：再尝试困难的 ∂l/∂a (注意力放在下图红色部分)

 

 

一次性得到 ∂l/∂a 的表达式真的很困难，因为从 a 开始后面每层的分数都和 a 有关，直到最后一层 l。那么我们就先只往前看一层，根据链式法则情况 2 (见小节1.8) 轻松得到上图的红色公式。

将 2.1 和 2.2 步得到结果综合便可推出下式

它最美妙的地方就是蓝色的偏导数

• ∂l/∂a 是前一层的 l 对分数 z 的偏导数

• ∂l/∂p 和 ∂l/∂q 是后一层的 l 对分数 p 和 q 的偏导数

这样递推关系就建立起来了。

 

第 3 步：再往前试一层如何？

 

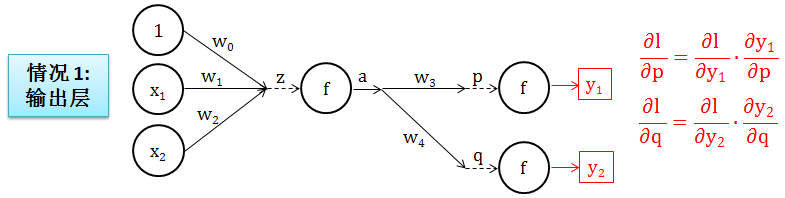
情况 1：如果到了输出层，我们就到头了，因为 ∂l/∂p 可以显性写出。而这是因为 ∂l/∂y1 可以显性写出 (试想损失函数 l 是 y 的平方差函数)，也因为 ∂y1/∂p 可以显性写出 (y1 是分数 p 经过转换函数 f 加工出来)。上述所有推理对 ∂l/∂q 也适用。如下图所示：

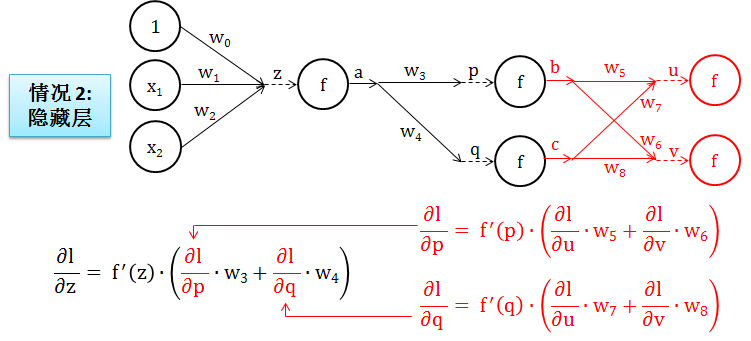
情况 2：如果还是隐藏层，再重复一遍第 2.2 步的过程，如下图所示：

好消息是：一直就像情况 2 这么递推下去，总有一次会遇到情况 1，那时就大功告成了。

复杂推导

讲完简单例子后，我们来严谨的证一遍反向传播吧。将注意力锁定在第 L 层，在严谨推导之前，让我们来热热身看看证明中需要用到的三个重要公式 E1, E2, E3。

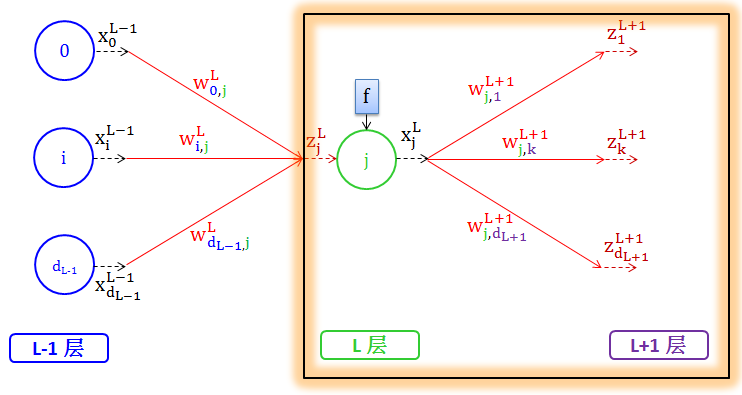
热身 1：从 L-1 层的输出到 L 层的分数，在转换成 L 层的输出，如下图橙色方框里：

E1：多变量线性函数的偏导数

E2：转换函数的导数

热身 2：从 L-1 层的输出到 L 层的分数，在转换成 L 层的输出，如下图橙色方框里：

E3：多变量线性函数的偏导数

热身完后，铭记 E1, E2, E3 这三个公式，带着它们来到反向传播的证明。

 

---

证明开始：如果你相信我的数学，你可以忽略这一段而直接用上式

第一步：明晰证明思路

第一步解释：

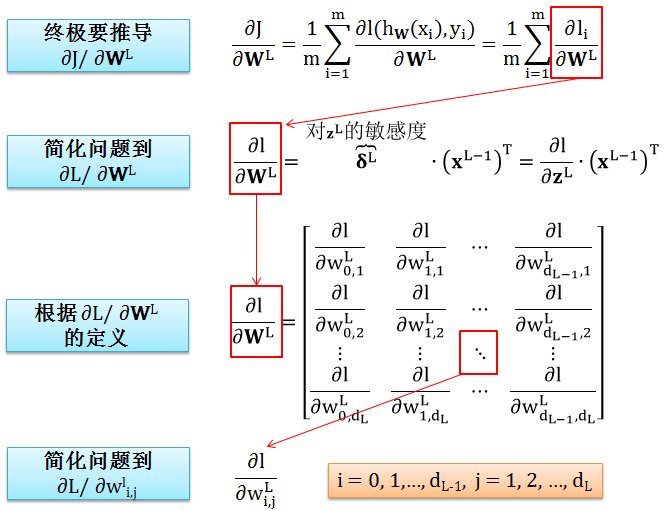
代价函数 J 是损失函数 l 的简单加总，J 对参数 WL 的偏导数可以分解成

 

 

由于累加符号里面各项对应的是各个样例，它们是完全平行，因此只需弄懂其中某项 ∂l/∂WL 即可。目标就是证明以下公式：

 

由于 ∂l/∂WL 是矩阵，将其进一步拆分成 ∂l/∂wLi,j。即一个纯量权重 wLi,j。

 

第二步：明晰核心过程

 

 

第二步解释：

 

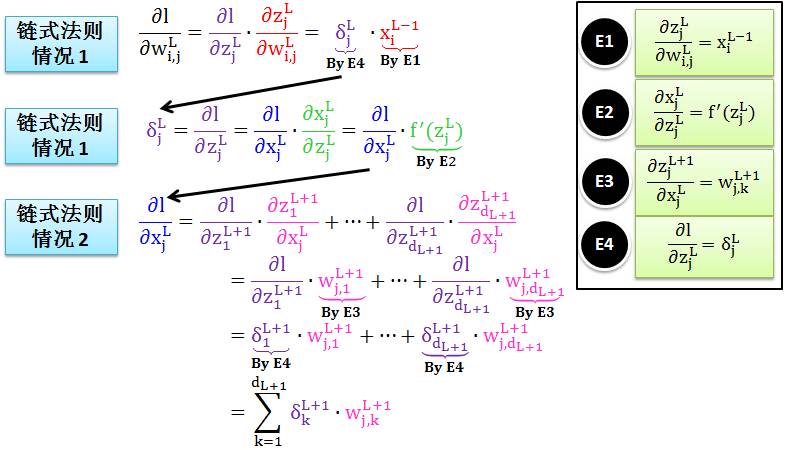
根据链式法则情况 1 则有公式 1

红色项已解决，再从紫色项敏感度定义开始，根据链式法则情况 1 则有公式 2

绿色项已解决，再从蓝色项开始，根据链式法则情况 2 则有公式 3

其中第二行根据 zkL+1 的表达式，第三行根据 δkL+1 的定义，第四行用累加符号简化表达式。

将公式 3 代入公式 2 得到 公式 4

现在看公式左右两边，我们已经建立了 L 层和 L+1 层的敏感度的关系，即用“L+1 层 dL+1 个敏感度 δkL+1”来表示“L 层 1 个敏感度 δjL”。

由于这个迭代关系是从后往前递推，因此需要一个最终条件 δjM (j = 1,2, …, dM)，称为公式 5

结合公式 4 和公式 5 得到

第三步：整理矩阵形式

将公式 4 里 δ 的纯量形式写成矩阵形式得到

将公式 5 里 δ 的纯量形式写成矩阵形式得到

有了 δ 矩阵形式，根据 ∂l/∂WL 的定义和公式 1 有

证明结束：那些忽略证明的读者可以重新上车

---

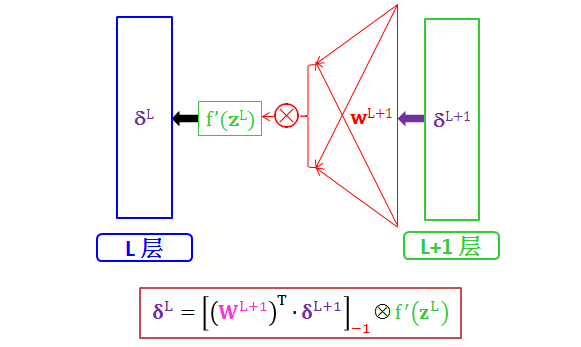
从 L+1 层到 L 层反向传播算法，其流程图如下:

该流程图表达的意思是：

1. L+1 层敏感度 δL+1 乘以L+1 层权重 WL+1 的转置，去掉第一个元素得到一个向量 V

2. 向量 V 每个元素乘以转换函数导数 f’(zL) 每个元素得到 L 层敏感度 δL

弄懂 L+1 层到 L 层反向传播算法之后，将 L 从 M-1 列举到 1 会不会？当然第 M 层就是输出层，需要做初始化。

第三章 - 实践狼

3.1

问题描述

用只带一层隐藏层的神经网络来识别黑白的手写数字 (如下)。

数据集有 5000 个示例，上图是随机打印出来其中的 100 个：

• 每一数字由 20×20 像素 (400 个像素) 组成

• 每个像素是一个实数值，代表着对应点上的灰色强度

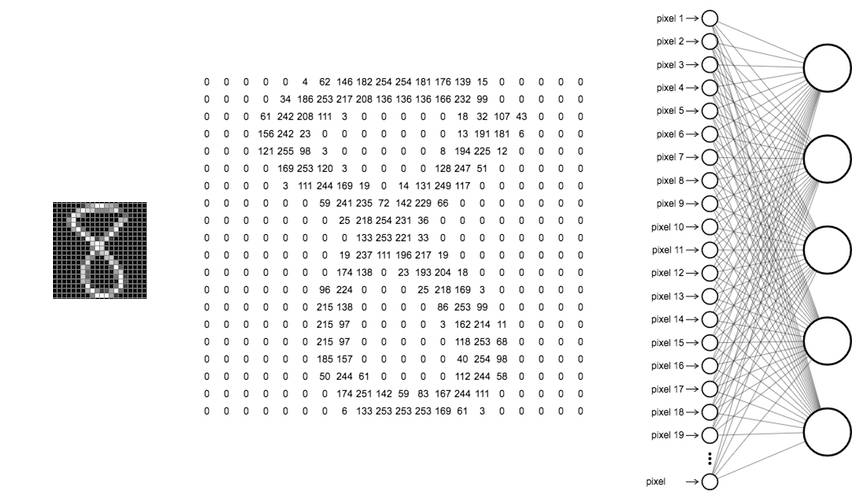
下图展示如何将数字 8 的照片分解成 400 个像素，并将这 400 个像素对应的灰色强度值作为神经网络的输入层上的 400 个节点。

3.2

数据解析

接下来，我们需要把“手写图片原始数据格式”转换成“Matlab 接收的数值格式”，在 Matlab 里：

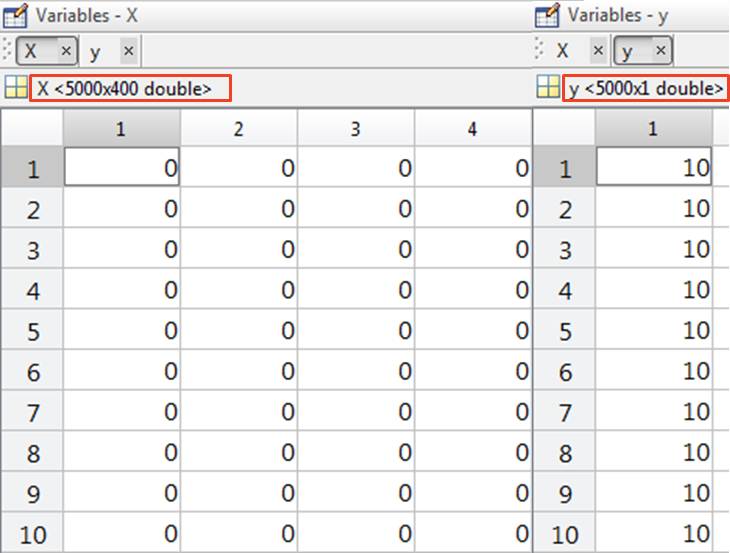
• 用矩阵 X 代表整个数据集的输入 (input)，将 20×20 像素的网格“展开”成 400 维的向量。每一个示例的输入是 X 的一行，那么 X 的大小是 5000×400

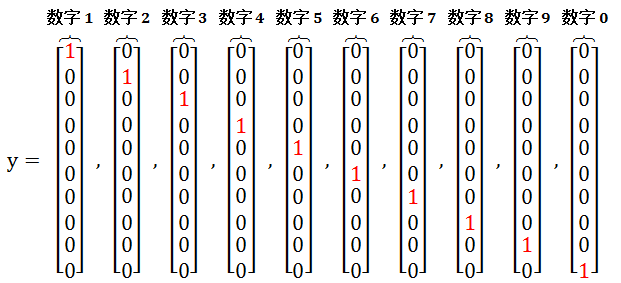
• 用列向量 y 代表整个数据集的标示 (label)，用 1 到 9 来标记“数字 1 到 9”，用 10 来“标记数字 0”。每一个示例的表示是 y 的一个，那么 y 的大小是 5000×1

X 和 y 的部分数值展示如下，主要是关注它们的大小 (红框里)

需要注意的是，将“手写图片原始数据格式”转换成“Matlab 接收的数值格式”需要一些工作，我们这里就假设有人帮我们把这些工作做好了，我们已经有现成的 X 和 y 供神经网络来把玩了。接下来我们需要编写一个函数，它的输入是 {权重，每层节点个数，图片像素，图片数字，惩罚系数}，输出是 {代价函数值，梯度}，函数如下：

    [ J, grad ] = ANN_CF( W_vec, node_size, X, y, lambda )

代价函数值 J 是由正向传播算出，而梯度 grad 是由反向传播算出。在接下来两小节，我们先不考虑正规项的惩罚系数 lambda 的问题，或先简单认为它等于 0。

3.3

正向传播

由于函数 ANN_CF 的输入变量 W_vec 是一个非常长的一维向量，为了之后运算方便，我们用 vec2cell 函数先将向量 W_vec 转换成元胞数组 W_c。

    W_c = vec2cell( W_vec, node_size );

元胞数组的意思就是 W_c 有 n 个元素，每个元素都可以是一个大小不一的矩阵。完整代码如下：

其中

• m 是图片个数 5000 个

• M 是元胞数组 W_c 的个数，也就是神经网络的层数

• vec1 是元素都为 1 的向量

 

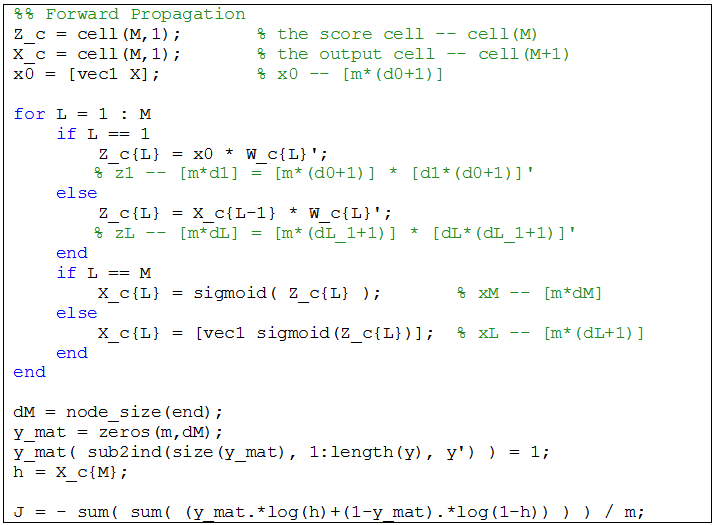
根据小节 2.1 的算法 1 ，我们在 ANN_CF 里面编写如下的正向传播代码：

上面代码的注释已经非常详细了，跟着小节 2.1 的流程图和算法看很容易看懂的。除了

 

    y_mat(sub2ind(size(y_mat), 1:length(y), y') ) = 1;

大家肯定觉得奇怪，从小节 3.1 可知 y 的大小是 5000×1 不是应该是个向量，怎么在这里变成一个矩阵了呢？原因是用独热编码 (one-hot encoding)，用 10×1 的向量代表数字 i，而该向量第 i 个元素是1，其它元素为 0。如下图所示：

而这是 y_mat 大小为 5000×10，处始值每个元素都是 0。根据上面独热编码将数字转化向量这一过程，那么应该给 y_mat 每一行 [1:length(y)] 的第 y 列 [y’] 赋值 1.  Matlab 的 sub2ind 就可以完成这样的赋值。

    y_mat(sub2ind(size(y_mat), 1:length(y), y') ) = 1;

3.4

反向传播

根据小节 2.3 的算法 2，我们在 ANN_CF 里面编写如下的反向传播代码：

上面代码的注释已经非常详细了，跟着小节 2.3 的流程图和算法看很容易看懂的。

3.5

梯度检验

用反向传播算完梯度后存储在 W_grad_c 元胞数组里，需要将它们每个变成一维向量再串联起来成为一个巨长的一维向量。代码如下：

其中 arrayfun 是将“元胞数组变成向量”这个操作应用在每个 W_grad_c 的元素上，由于该操作的 output 是大小不同的 array，因此'UniformOutput'应该设为 false。

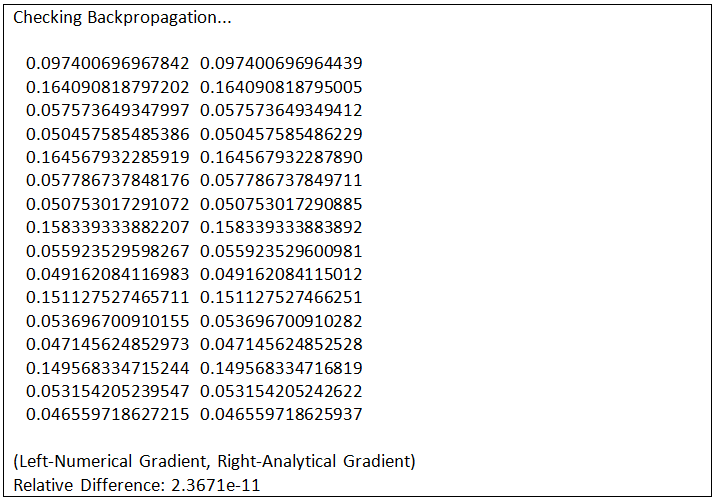
用反向传播算出梯度后，就可以用梯度下降来最优权重了。但是怎么能保证反向传播算出的梯度就是对的呢？一个有效的方法就是用有限差分 (finite difference) 来数值解的梯度 F，和反向传播算出的梯度相比。过程如下：

将上面数学表达式转成代码得到：

部分测试结果如下：

3.6

其它技巧

现在整套训练 ANN 的程序基本上大功告成，除了两个问题：

 

1. 如何给定权重 W 的初始值?

2. 如何防止神经网络过拟合？

 

第一个问题好解决，根据牛人经验，wL 初始值为

代码如下：

第二个问题需要引入正规项 (类似于岭回归和线性回归)

其中

• λ 是正规项的惩罚系数，是一个超参数 (hyper-parameter)

• 蓝色项指的是 W 里面每个元素乘以每个元素的和 (剔除偏差项)

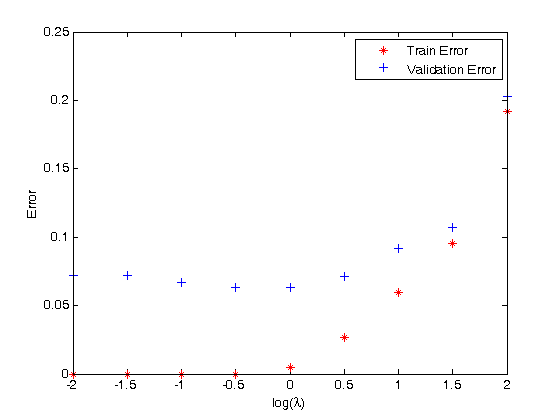
为了选择最优 λ，我们将 5000 个数据集随机分成 4 比 1，4000 个用做训练调权重，1000 个用作验证选 λ，给定一组 λ = {10-2, 10-1.5, 10-1 …,10, 101.5, 102}，画出训练误差和测试误差：

我们发现

• 训练误差随着 λ 增加而增加，在 λ 小于 1 是训练误差几乎为 0

• 验证误差随着 λ 增加先减小在增加，在 λ 等于 100.5 是最低，大概 7% 左右

这结果对于一个只有一层隐藏层的 ANN 来说，还可以。

总结

ANN 的正向传播 (forward propagation) 和反向传播 (backpropagation) 其实非常简单。

• 正向传播就是把权重当已知量从头算到尾得到输出值

• 反向传播就是把权重当未知量从尾推到头得到偏导数

 

而计算权重，或调ANN参数的过程可以看成是以下三步：

1. 用正向传播计算预测值 (以一种权重的函数形式)

2. 用反向传播计算梯度值 (用到上一步的预测值和真实值)

3. 用批量或随机梯度下降法求出最优权重

 

刚写完这篇反向传播的文章，突然看到深度学习教父 Geoffrey Hinton 要将反向传播全部抛掉重头再来。反向传播中需要给所有数据打上标签，然后通过逐层调整权重而最小化代价函数。但是 Hinton 认为

这不是大脑的工作方式，大脑显然不需要所有的数据都打上标签。为了能使神经网络更聪明，也就是更好的发展“无监督学习”，就意味着要摆脱反向传播。

哎，真是跟不上大牛的脚步啊。。。

到本篇为止，基本上监督式学习 (supervised learning) 的问题都讲完了，包括：

 

• 线性回归 (linear regression)

• 多项式回归 (polynomial regression)

• 岭回归 (ridge regression)

• 套索回归 (LASSO regression)

• 近邻回归 (nearest neighbor regression)

• 局部加权回归 (locally weighted regression)

• 对率分类 (logistic classification)

• 多项对率分类 (softmax classification)

• 高斯判别分析 (Gaussian discriminant analysis)

• 朴素贝叶斯 (naïve Bayes)

• 决策树 (decisiontree)

• 随机森林 (random forest)

• 梯度提升树 (gradient boosted tree)

• 支撑向量机 [1] [2] (support vector machine)

• 人工神经网络 (artificial neural network)

此外还讲了

• 机器学习的定义 (ML definition)

• 模型评估和选择  (model assessment and selection)

• 集成方法 (ensemble method)

• 计算学习理论 (computational learning theory)

• 4 篇 python 编程实战篇 [1] [2] [3] [4]

 

回首一看，居然写了这么多干货，下篇 (虽然不知道是何时) 开始非监督式学习(unsupervised learning) 的里程。Stay Tuned！