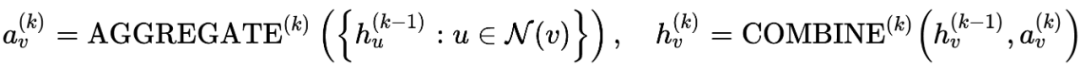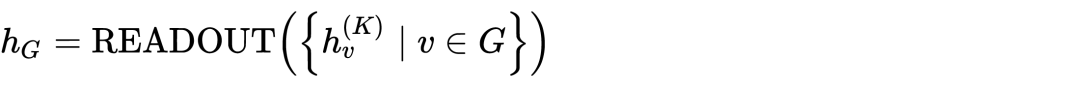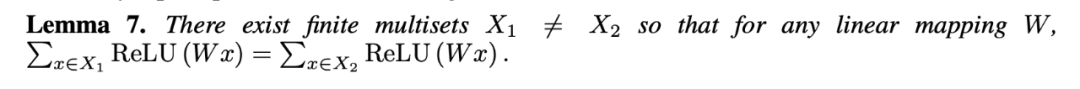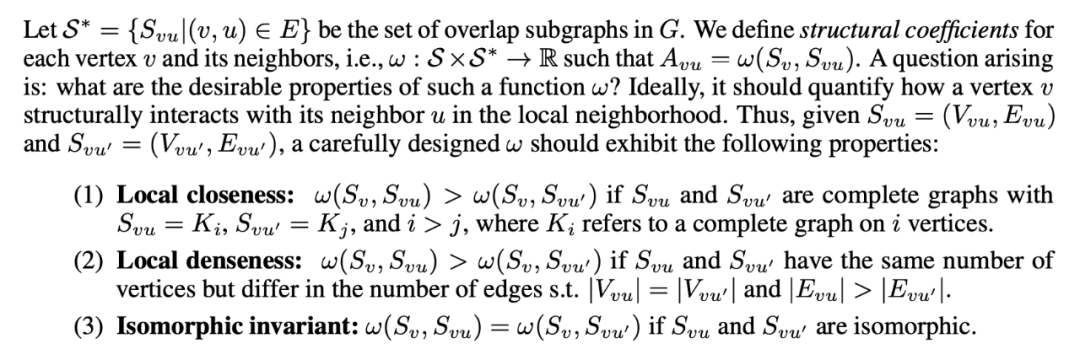从ICLR 2022看什么是好的图神经网络？

©作者 | 刘雨乐

学校 | 上海科技大学

研究方向 | 机器学习与图神经网络

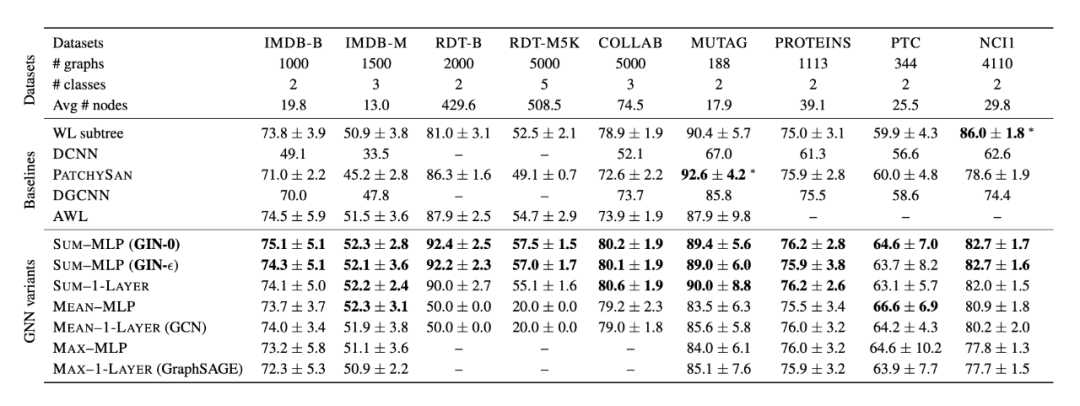
什么是好的 GNN？如果仅仅是用数据集上的测试结果，实际上是一种不太公正的结果。第一，网络可能只对某一种数据集效果好；第二，网络可能是经过玄学调参优化后对某些数据学习能力较强。实验导向的质量分析终究不如有一套理论的来的实在，Keyulu 大神基于 WL-test 给出了一套检验框架。

Xu, K., Hu, W., Leskovec, J. and Jegelka, S., 2018. How powerful are graph neural networks?. arXiv preprint arXiv:1810.00826.

所谓 WL-test 即为一种检验异构图的测试，与 GNN 相似，WL-test 也是迭代的的更新节点的特征，就像 GNN 的聚合-结合（Aggregate-Combine）的过程一样，他可以把不同的图编码为不同的 embedding，而异构图变成相同的；相反，对于一个 GNN 来说，很难把异构图映射到同一个 embedding。作者指出，一个 GNN 不可能比 WL-test 更有效也是基于此。究其根本，WL-test 得到的 embedding 是一个从原图的单射。所以我们要得到一个提取特征能力强大的 GNN，最基本要做的就是创造所谓的从图到 embedding 的单射。

但是有趣的是，ICLR 2022 的一篇新论文发现了比 WL-test 更强大的框架，有待继续看。

基本思路明确了以后，就是要开始建模了。

首先是 GNN 的基本框架，从邻居聚合（Aggregate），把聚合后的的特征与上一层的特征结合（Combine），如有需要，最后对全图进行聚合（Readout）即可。

我们所熟知的 Graph Sage 和 GCN，GAT 本质是更换函数。所谓的 Spectral 和 sptial 的观点，不过是之前没有了解清楚罢了。

其次是为了证明结果的理论框架，论文的 theorem 其实都非常直观：

1. 单射最强定理：

这里是最基本的东西，即信息传播时聚合，必须是一个单射；全图读出时，也必须是一个单射，这样就保持了 WL-test 的特性。

2. sum-单射引理

即，我们使用 sum 进行聚合是一个符合条件的单射。

3. 构造模型，基于上述符合的条件，可以构造一种特殊的 GNN，作者将其命名为  GIN（graph isomorphic network）

实际上，只要是符合条件的网络还可以构造相当多个。

关于全图的 readout，作者选择把每一层的信息都聚合连起来，是因为较前方的聚合的信息往往更有用，其实这里的设计应该是像 Resnet 一样的东西。

除了自己的模型，作者还分析了其他的模型

1. 对于 GCN 而言，聚合函数（Aggregate）选用一层的 MLP，这并不是一个单射，为什么还能达到不错的效果呢？MLP 本身就是有模拟任何函数的功能，这其实相当于近似了一个 sum，但是肉眼可见的，会有许多不能达到的情况，因此不能达到更好的表现。

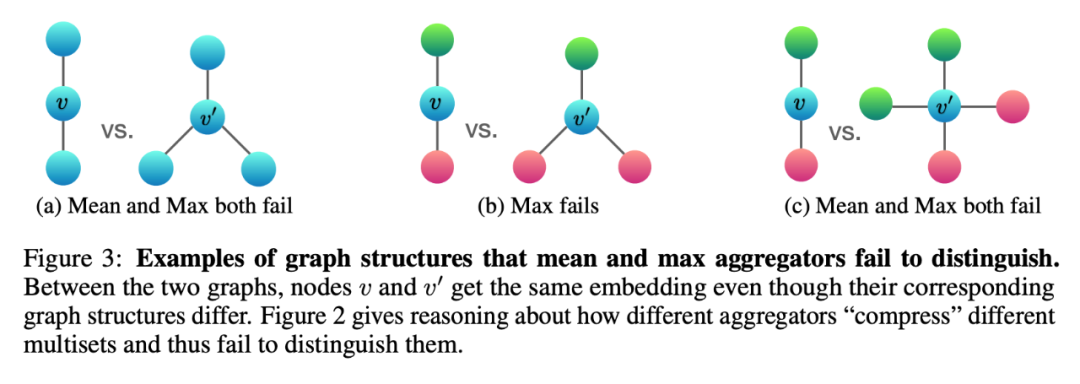
2. 关于 MEAN-aggre 和 MAX-aggre 的缺陷：

不同颜色代表不一样的特征，动手算一算就可以知道这些图用 max 或者 mean 或多或少会不能区分，因为传递到中心节点的信息是完全一样的。

3. 特别的作者还指出，mean 和 max 有他们独有的情景，这些情境中可以达到好的效果，主要是因为不会有错误出现。

如果分布不同，mean 就不会出现误判；

如果节点之间互不相同，max 就会有效。

还有其他的两个，GAT 的带权重的特征和 LSTM 的池化，作者没分析，估计是没时间了，理论上也能证出来。

理论上好的东西，简单的模型也能达到好的效果。

上一章节，说到什么是好的图神经网络，keyulu et al. 认为如果把聚合和全图读出加以修改，使得能成为一个单射的话，那么 GNN 就可以达到和 1-WL test 同等的效果。

后来的工作也大多由此为基础展开，大致分为三个方向：

1. 最朴素的想法，用 GNN 模拟更高阶的 WL-test，就好比 GCN 出来后不少人试了更高阶的切比雪夫不等式，准确率变高但是运算量却变大很多

2. 提取一些子结构如 cycles，d-regular graphs 作为新的特征进行训练

3. 增强节点的特征或者引入随机特征来分析

这些工作重要，但是并没有跳脱现有框架。

ICLR 2022 的论文 A NEW PERSPECTIVE ON"HOW GRAPH NEURAL NET-WORKS GO BEYOND WEISFEILER-LEHMAN?"

@inproceedings{
wijesinghe2022a,
title={A New Perspective on ''How Graph Neural Networks Go Beyond Weisfeiler-Lehman?''},
author={Asiri Wijesinghe and Qing Wang},
booktitle={International Conference on Learning Representations},
year={2022},
url={https://openreview.net/forum?id=uxgg9o7bI_3}
}

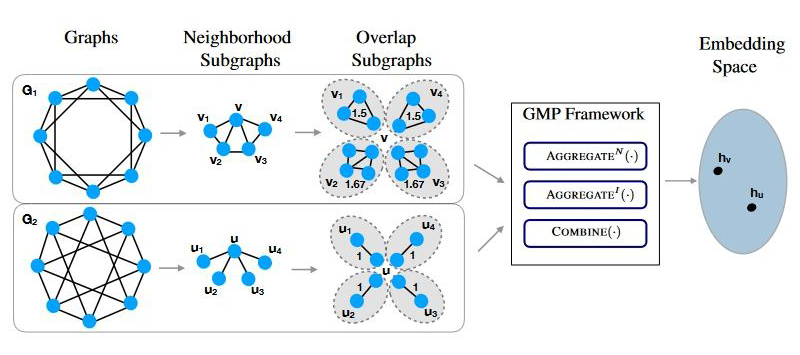
重新把很久之前的的 spectral 和 sptial 的方向作为切入点，spectral 考虑了拓扑结构，而 GAT，GIN 等一系列方法聚合时本质还是把拓扑结构上的东西扔掉了，所以作者基于此，从信息传递的框架出发，定义了关于图拓扑结构的特征进行聚合，成功把 spectral 和 sptial 两种方法考虑的出发点都融合进去了得到了现在这篇文章。

考虑 1-WL test，下图是一个其失效的例子：

邻居都一样，但是邻居之间有不同，所以简单的聚合就失效了。为了刻画这种邻居间的关系，作者引入了一套新的理论体系：

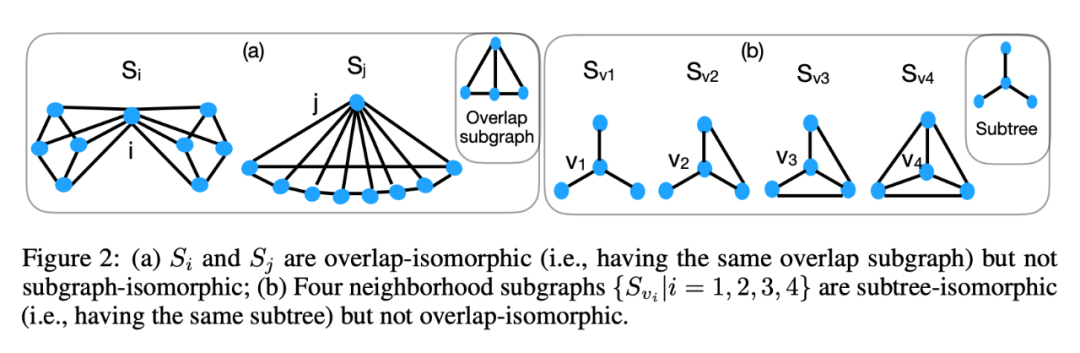
到了喜闻乐见的新定义环节，这些定义很烦，说人话就是：

邻居子图： ：一个点和他的邻居还有对应的边

重叠子图： ：两个邻居子图 and 的重叠部分

子图异构（1）：两个图完全一样（连接方式）

重叠异构（2）：重叠部分一样

子树异构（3）：接邻的节点一样，边可能不一样

下面是一个例子来验证这些定义：

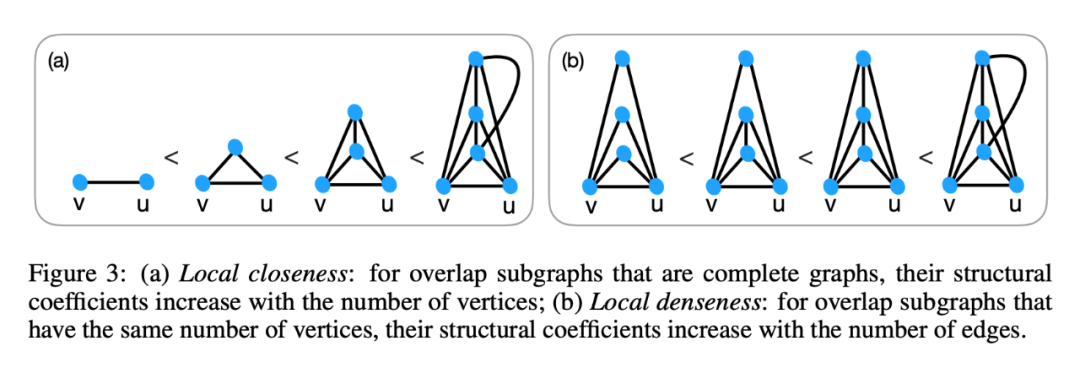
显然的，这三种异构的一个包含一个，1 最小，3 最大。

有了这些我们就有一个直观认识，量化一个节点和他邻居的关系，要考虑他们之间的紧密程度，就要从这三种异构的角度去考虑，其中重叠的子图能最好的描述节点和某一邻居的关系，自然的，我们需要引出这样的参数 omega，应该有如下的性质：

1. 重叠子图是完全图的，最强，完全图越大越强

2. 节点相同，边越多越强

3. 重叠子图一样，这两个权重也一样。以下是两个例子：

然后做聚合，这下就要把刚才定义的参量 A 拿进来，就形成这样的框架：

这里就是实践部分了，前向传播时还是为了保证单射，采用了 sum 的 combine 方法，和 GIN 还是很像的，主要创新点就是把结构信息量化并且塞进了聚合的函数。前面理解了看到这里只剩感叹这种 omega 是怎么设计出的。

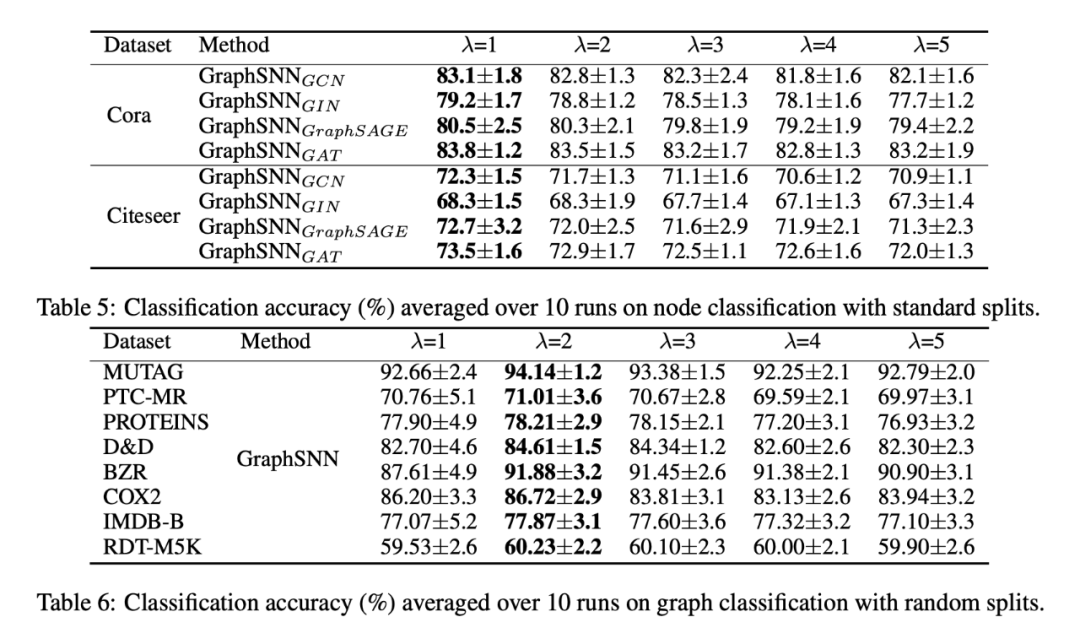
消融实验：研究了不同的 lamda 的特点，发现为 1 时，更多考虑的是不同节点的的特征，适用于节点分类；为 2 时，考虑的的时重叠图的相似度，适用于图分类。下标的意思是仅仅修改下标网络结构的聚合方式，其他的部分不变得到的结果

举个例子，具体可以到论文的附录看，这篇文章附录真的很多：

过平滑的分析：

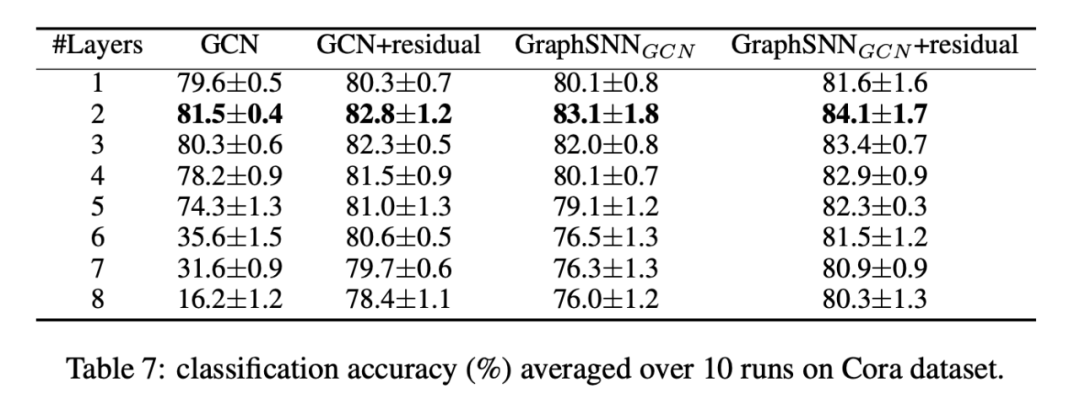
这个玩意相比 GCN 对更多的层数时更耐草，因为描述邻居连接关系的的参数 omega 本质上就是一个带有不同权重的特征，这个限制了连接紧密程度不同的的邻居流过来的信息，有效防止了过平滑。

还是那句话既有 spectral 又有 spitial，应该是两种理念第一次交融，所以效果格外的好。

插一嘴，看看 openreview 真的有用，前提是 ICLR 这种顶会：

https://openreview.net/forum?id=uxgg9o7bI_3

特别鸣谢

感谢 TCCI 天桥脑科学研究院对于 PaperWeekly 的支持。TCCI 关注大脑探知、大脑功能和大脑健康。

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·