快来看！诺贝尔经济学奖得主教你如何构建投资组合啦！

我们在之前《一文教你如何最优化投资组合》和《定量描述估计误差，让你离最优投资组合更近一步》中描述了如何拓展运用均值方差模型优化我们的投资组合。本文我们追本溯源，介绍一下均值方差模型的基本形式以及衍生形式，并说明萝卜投资如何使用均值方差模型来完成投资组合的构建。

均值方差模型——华尔街的第一次革命

经典模型

我们都知道，均值方差模型源于马科维兹于1952年发表在《Portfolio Selection》论文，论文中他引入了均值和方差的两个统计学概念，用定量的手段进行投资组合的选择。 均值和方差分别代表了投资者预期获得的收益和所承担的风险。 我们用下面这个式子来表示投资组合的选择过程：

我们称这样的最优化形式为最大化效用函数，用户需要输入他自身对风险厌恶的程度，同时在输入一些必要的约束条件，例如个股的权重界限，就可以让优化器进行求解了。

模型变形式

效用函数是均值方差模型的经典形式，不过我们可以给出另外四种形式，他们是均值方差模型的变种。 他们分别是，给定风险最大化收益、给定收益最小化风险、最大化夏普比率和最大化信息比率。

给定风险最大化收益：用户可以精确地控制他的投资组合所达到的风险水平，基本形式为

萝卜投资中均值方差模型的运用

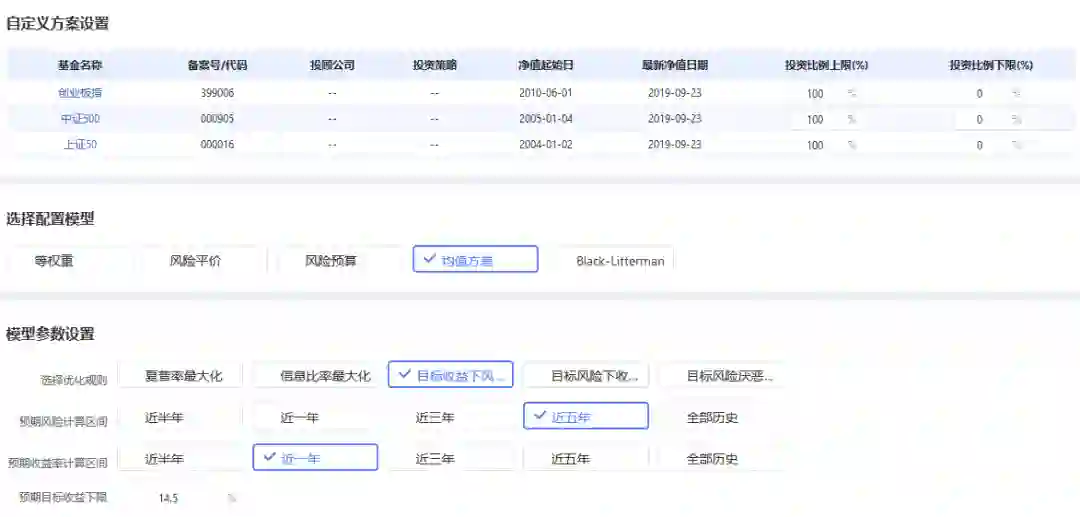
这里我们选择的资产分别是上证50、中证500和创业板指，采用均值方差模型中的目标收益下风险最小化，预期风险和预期收益率计算区间分别选择了近五年和近一年，表明使用这些标的对应时间段内的收益率数据来计算r和V，同时设置了预期目标收益下限为14.5%。

图1： 模型参数设置

来源： 萝卜投资

我们可以得到以下配置结果：

图2： 模型优化结果

来源： 萝卜投资

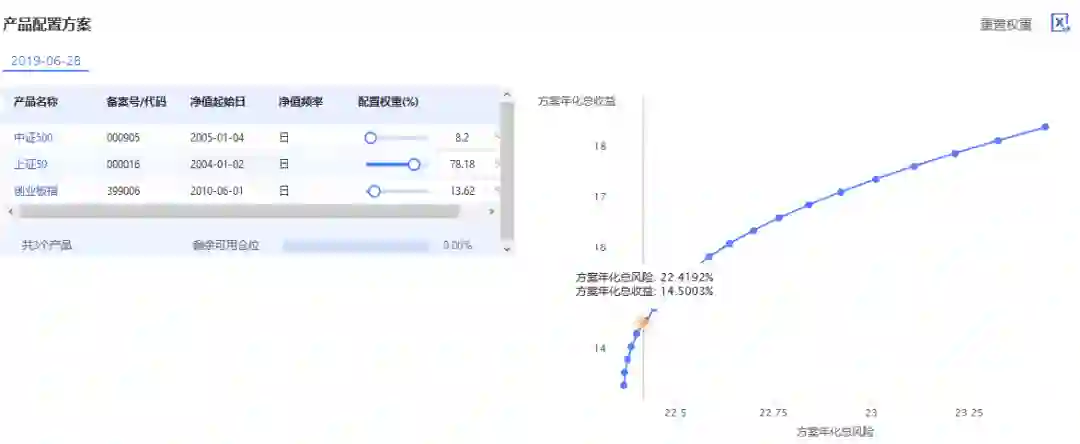
图2左边表示投资组合中各资产的权重比例，右边的黄点即为我们优化后的组合，以及它在有效前沿上的位置。 通过黄点上浮起的窗口可知，这个组合的预期年化收益14.5%，符合我们预先设置的约束条件。

对于另外四种模型，我们只需要稍微修改一下和模型相关的参数，就能使用对应的模型进行优化求解。

本文介绍了均值方差模型背后的理论方法，并且演示了如何在萝卜投资完成对应的资产配置。 随着智能投资时代的来临，人们对于科学投资提出了更高的要求，均值方差模型作为经典的定量投资方法，至今仍然活跃在学界和工业界，每年都有非常多相关的论文产出，以后有机会再一一介绍。