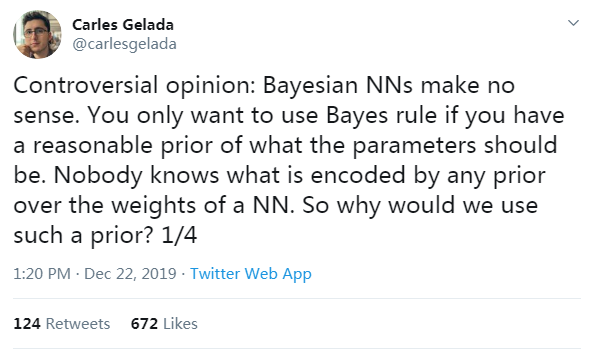
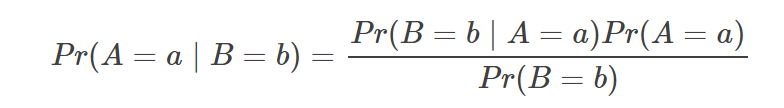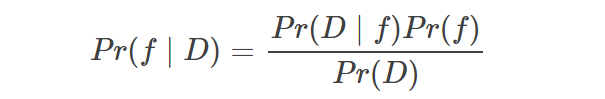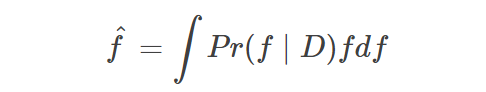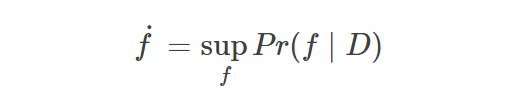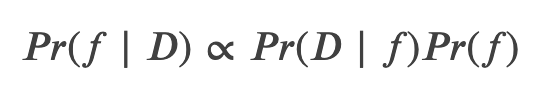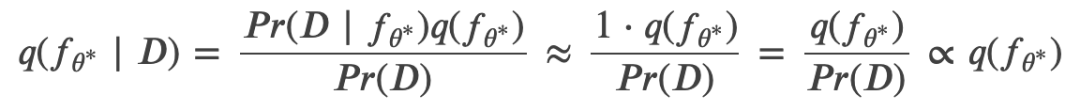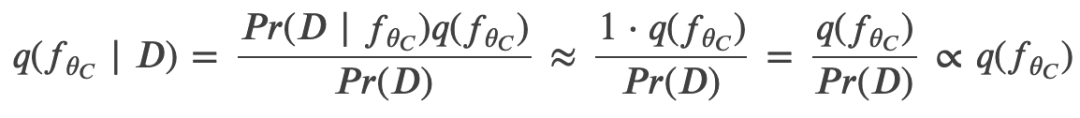纯贝叶斯神经网络没有意义？OpenAI科学家何出此言？

选自Buckman's Homepage

作者：C arles Gelada、Jacob Buckman

机器之心编译

参与：魔王

近日，OpenAI 研究科学家 Carles Gelada 发布推文，表示「贝叶斯神经网络没有意义」。一石激起千层浪，社区对此言论展开了激烈的讨论。那么贝叶斯神经网络真的没有意义吗？Carles Gelada 何出此言？我们来看这篇文章。

2019 年 12 月 22 日 Carles Gelada 发布的推文。推文链接：https://twitter.com/carlesgelada/status/1208618401729568768

Carles Gelada 和 Jacob Buckman 认为推文下面的大部分回复忽略了他们对 BNN 批评的重点，于是撰写博客，更加全面地阐述其观点。

以下是标题为《Bayesian Neural Networks Need Not Concentrate》的最新版博客内容 （原版博客标题为《A Sober Look at Bayesian Neural Networks》）：

贝叶斯神经网络的支持者经常称，训练得到的 BNN 输出分布能够捕捉认知不确定性（epistemic uncertainty）。认知不确定性对大量应用具备宝贵价值，我们认同使用贝叶斯方法的做法。但是， 我们认为 BNN 需要信息丰富的先验才能处理不确定性 。我们证明，如果先验不能区分可泛化和不可泛化的函数，则贝叶斯推断无法提供有用的不确定性。这就对标准论点提出了质疑，标准论点即：当真实先验分布未知时，「信息不足的先验」是合适的。

什么是贝叶斯推断？

在 Twitter 讨论中，很多研究者认为「贝叶斯」是「不确定性感知」（uncertainty-aware）的同义词，或者使用结果集合或分布的算法一定是贝叶斯算法。我们想要厘清一点，在我们看来，这种描述有失公允。

使用贝叶斯方法处理不确定性，需要利用贝叶斯定理将先验分布更新至后验分布中，这无疑是最流行的方法之一。但还存在其他非贝叶斯方法，例如集中不等式就是非贝叶斯方法，它们允许计算置信区间和不确定性集合。

贝叶斯定理的核心是条件概率分布之间的关系：

毫无疑问，这是非常强大且基础的关系，但任何「信念更新」（belief updating）或「可能世界分布」（distributions over possible worlds）的概念都只是后此谬误（post hoc）的解释。贝叶斯定理表示：对于任意两个非独立随机变量 A 和 B，当 B 取特殊值 b 时，随机变量 A 的分布发生改变。用标准学术语言来说，项 Pr(A=a) 即先验，Pr(B=b∣A=a) 是似然，Pr(A=a∣B=b) 是后验。该用语来源于这一事实：随机变量 A 具备原始（先验）分布，使用观测到的 b 值可提供更新分布（后验）。

我们来想一下如何使用贝叶斯框架解决分类问题。

存在输入空间 χ 和输出空间 Y，假设它们均为离散空间，存在函数族 f:χ→T 是二者之间的映射。将每个 f 看作向量 f∈Y^χ，在索引 x∈χ 处索引向量相当于估计函数 f_x=f(x)。存在我们感兴趣的真值函数 f^∗:χ→Y。用贝叶斯方法解决该问题，即在现实世界中存在随机变量 F^∗，f^∗ 是其中的一个样本。

我们将使用 Pr(F^∗=f) 表示 F^∗ 的分布。（下文用缩写形式 Pr(f) 表示 Pr(F^∗=f)）。由于输入-输出对数据集 D={(x_i,F^∗(x_i)} 不独立于 F^∗，因此我们可以使用贝叶斯定理来了解 F^∗的分布，前提是我们已经观察了数据集 D。

项 Pr(D∣f)=∏_(x,y∈D)1_f(x)=y 表示：如果 F^∗=f，则数据集包含的标签等同于 f 的输出。这一条件分布为什么这么有趣？因为如果数据集包含足够信息，则 F^∗ 的分布可能崩塌到一个点，我们可能不具备对 f^∗ 的不确定性。即使分布没有崩塌到一个点，我们仍然可以利用 Pr(f∣D) 执行一些有意思的操作。例如，我们可以通过边缘化（marginalizing）来提供估计结果：

或者找出后验估计的最大值：

但更有趣的是，我们可以利用分布来提供不确定性：特定输出 f^∗(x) 的分布。给出测试点 x，我们可以输出概率 Pr(F^∗(x)=y∣D)。这非常重要，例如在很多敏感应用中，在不确定的情况下不执行预测是十分必要的。截至此时，贝叶斯方法看起来很有吸引力。

贝叶斯神经网络的潜在问题

贝叶斯的以上所有属性均依赖于合理的后验分布，即向更有可能正确的函数分配更大的概率值。我们来仔细探查其中究竟。下式表示后验，不过由于分母 Pr(D) 只是标准化常量，对所有函数都是一样的，因此下式隐去了分母：

该式中有两个项：先验 Pr(f) 表示对特定函数的先验偏好，似然 Pr(D∣f) 将特定函数具备更强的数据兼容性这一想法进行编码。

标准的贝叶斯叙事是这样的：先验覆盖大量函数，但只有一部分函数与数据兼容，因此后验集中于一小部分函数，这些函数都有可能是合适的函数。

从这个角度来看，选择「信息不足的（uninformative）」先验是合理的做法，因为它在所有函数的集合上均匀分布。这就使得贝叶斯神经网络的基础得到保障，因为它确保先验向每个可能正确的函数分配非零概率。然后，我们只需让似然项筛除空间中的糟糕函数即可。看起来很简单吧！但是，标准贝叶斯叙事存在「隐藏条款」。

首先，我们需要注意， 不确定性估计的质量完全取决于先验的质量 。因此要想使后验分布对应可能函数的确切分布，先验必须完全正确。也就是说，采样真值函数 f^∗ 的分布必须与采样先验的分布相同。如若不然，则后验会很糟糕！

假设先验比现实更陡峭，那么很明显这是一个失败案例：后验某些区域的概率不恰当地低，导致整体不确定性被低估。当先验比现实平滑时，则失败没有那么明显，但仍会出现：对于任意固定数量的数据而言，学得的后验太宽了，导致不确定性被高估。或者说，需要更多数据才能达到特定的置信度。

其次，标准贝叶斯叙事几乎总是发生在参数不足（underparameterized）的情况下，即数据集∣D∣的规模至少与模型参数量一样。但是当我们使用神经网络时，实际设置显然并非如此。增加神经模型的规模总能帮助提升性能，因此我们总想使用过参数化机制。在思考贝叶斯深度学习时，我们需要仔细考虑该差异的含义。

不幸的是，这些事项结合到一起导致了一个重大问题：数据无法带来神经网络后验集中。

贝叶斯神经网络不需要集中

用神经网络（参数为θ）拟合数据集 D 常会导致这一常见情形，D 包含真值函数 f^∗ 生成的输入-输出对。当然，由于我们在做深度学习，因此使用过参数化机制较为稳妥：∣D∣<<∣θ∣。此外，我们假设网络足够灵活，可使真值函数 f^∗ 在它所表示的函数类别内。令神经网络函数 f_θ^∗ 逼近 f_θ^∗(x)≈f^∗(x)∀x∈χ。由于 f_θ^∗ 可以拟合每个数据点，因此它能够拟合 D 中所有点：Pr(D∣f_θ^∗)≈1。

不过，D 不是神经网络要拟合的唯一数据集。假设从同一个真值函数 f^∗ 的输入-输出对中采样得到数据集 Z={(x_i,y_i}，并损坏数据集中的部分输出，得到 Z˙={(x_i,y˙_i}，y_i≠y˙_i∀i。最终，将真实数据 D 和损坏数据 Z˙ 结合得到一个组合数据集 C。（假设∣Z˙∣较小，这样我们可以继续使用过参数化机制，即∣C∣<<∣θ∣。）Chiyuan Zhang 等人在 2017 年发表的论文《Understanding deep learning requires rethinking generalization》中证明，我们可以训练出完美拟合数据集 C 的神经网络，即 ∃θ_C s.t. f_θ_C(x)≈y,∀_x,y∈C。网络的容量不仅足以拟合正确的标签，还可以拟合任意损坏的标签！

理解 f_θ^∗ 和 f_θ_C 之间差异的直观方式是观察其泛化性。假设 D 是训练集，Z 是测试集。函数 f_θ^∗ 泛化性能优异：它在训练集上实现了不错的性能（即 Pr(D∣f_θ_C)≈1），在测试集上也取得了优秀的性能（即 Pr(Z∣f_θ_C)≈1）。而函数 f_θ_C 恰恰相反，其泛化性能并不好：它在训练集上表现不错（即 Pr(D∣f_θ_C)≈1），但在测试集上表现糟糕（即 Pr(Z∣f_θ_C)≈0）。按照经验，SGD 通常更可能找到泛化性能优异的解决方案，但是我们必须记住也存在泛化性能不好的解决方案。

现在我们已经定义了这两个函数。那么给定数据集 D，二者的相对后验概率如何呢？假设我们选择先验 q，则存在

类似地，

现在我们可以清晰地看到，为什么标准贝叶斯和神经网络结合后，问题多多了吧。f_θ^∗ 泛化性能较好，f_θ_C 泛化性能差，但我们通过后验概率无法区分二者的差异。这两个网络的相对后验似然完全由其先验似然决定。

SGD 能够拯救这一切吗？

不能。在数据集 D 上运行 SGD 不太可能找到 f_θ_C。但是这不表示它不存在。真正的贝叶斯后验是唯一一个具备我们追寻的有用属性（如不确定性信息）的对象，它并不关心 SGD 找到什么函数。令 q(f_θ_C∣D)<q(f_θ^∗∣D) 成立的唯一方式是 q(f_θ_C)<q(f_θ^∗)。

贝叶斯神经网络需要对泛化敏感的先验

现在很清楚了，正确的先验对贝叶斯深度学习而言是绝对必要的。我们所需要的是「泛化敏感」先验（generalization-sensitive prior），即仅对泛化性能优秀的函数分配先验概率。这与「泛化不可知」先验相反：对于按照上述方法构建的任意数据集 C，存在 q(f_θ^∗)≈q(f_θ_C)。如果我们的先验完全泛化不可知，则后验将对糟糕和优秀的解决方案分配同样的概率。这反过来说明，贝叶斯步骤没有收获有用的不确定性信息：每一个测试点的概率在全部可能输出中均匀分布。

一定程度上，这种现象可被解释为「过高估计不确定性」的极端案例。在标准贝叶斯叙事中，高估不确定性不影响大局，因为这不过说明我们需要添加一点数据让后验集中。但涉及过参数化机制时，「一点数据」就没用了。让后验集中所需的数据量非常庞大。（另外，即使我们能够获取那么多数据，我们也只能收获一个更大的神经网络而已，一切还是回到原点。）

目前的 BNN 对泛化敏感吗？

我们通常对 BNN 使用简单的先验，即权重的独立高斯分布。结合神经网络架构后，得到函数空间中的结构化先验。显然，该结构化先验并不简单。例如，Radford M. Neal 1995 年发表的论文《BAYESIAN LEARNING FOR NEURAL NETWORKS》证明，无限宽度单层神经网络的独立随机高斯权重对应高斯过程先验（Gaussian Process prior）。从实验的角度来看，Ulyanov (2017) 证明，CNNs + SGD 这一组合很擅长表示自然图像。我们做了一些实验来验证这一点，发现相比最小化模型在数据集 C 上的损失，最小化模型在数据集 D 上的损失能够取得更高的先验似然。

但是，这只是间接证据，并未击中问题的核心。如上所示，宣称「我的后验分布对应优秀解决方案的分布」的贝叶斯支持者实际上是在表达「我的先验对泛化敏感」。这一主张很强势，尤其是在简化当前先验的背景下。独立高斯权重真的能够编码泛化这么基础的东西吗，甚至还能考虑到网络架构？这是可能的，但对此持怀疑态度是更加明智的做法。贝叶斯社区有责任进行审慎分析和实验来充分证明此主张。

BNN 的实验成功是否证明其具备优秀先验？

不。尽管在实践中，BNN 确实泛化至测试点了，而且看起来也输出了合理的不确定性估计，但这无法直接证明它们具备泛化敏感的先验。这就要提到该难题的另一块拼图了：逼近（approximation）。计算 q(f∣D)q，即贝叶斯推断，是一个难题，因此社区中大量成员研究其易处理的近似问题。（例如，变分推断将 q(f∣D) 的计算问题形式化为优化问题。）为什么 BNN 在真实后验极其不确定的情况下也能作出一些合理的行为？计算 q(f∣D) 是关键。它们可能并没有学习任何接近真实后验的事物！

要想声称 BNN 输出的不确定性有效，贝叶斯支持者必须谨慎地证明 BNN 学到的分布类似真实后验。初始实验证明事实并非如此：我们可以轻松找到这样两个点，第一个点具备较高的先验概率和数据似然，第二个点具备较高的后验似然。如果 BNN 后验准确，就不会出现这种情况。代码地址：https://github.com/jbuckman/bnn-blog-experiments

不过，这只是初步实验，还需要更多研究。

批判地看待贝叶斯神经网络

近几十年来，贝叶斯社区输出大量有关机器学习的重要见解，通常被认为是最严谨的机器学习子社区之一。但是，我们认为贝叶斯神经网络并不符合这一看法。贝叶斯社区并未对「BNN 输出分布很好地对应真实后验」提供证明。没有该保障，则 BNN 与其他神经网络无异。因此，研究人员应该避免发表「BNN 输出分布能够编码模型不确定性」这样的观点。

此外，我们证明了好的不确定性估计必须围绕神经网络的泛化性能。要想确保 BNN 提供的不确定性有用，我们首先需要了解使特定神经网络参数取得优秀/糟糕泛化性能的原因。这是深度学习领域最重要的问题之一，但我们以及整个领域对此还没有深刻理解。神经切线核（该方法也得到贝叶斯的支持）是一种有前景的方法，有助于研究者真正地理解泛化。而只有理解了泛化，我们才能设计泛化敏感先验。

不管你是否相信我们能够找到优秀的泛化敏感先验，重点在于： 我们以及整个领域不再忽略先验在贝叶斯框架中的重要性，不要想当然地认为 BNN 是计算不确定性的好方法。 我们需要批判地思考先验，严谨地评估后验估计，不被「信息不足的先验仍然能够带来优秀的不确定性估计」这样的粗陋论点所支配。

现在，没有人去问 BNN 能否提供当前最优的不确定性估计，有的是使用 BNN 的理由（尤其是在经验驱动的领域，如深度学习）。但我们需要理解，即使有理由证明 BNN 前景广阔，但也有清晰的理论可以证明 BNN 或许不能作为研究方向。本文希望强调这些潜在的问题，从而引导 BNN 研究走在更好的方向上。

原文链接：https://jacobbuckman.com/2020-01-22-bayesian-neural-networks-need-not-concentrate/

原版博客链接：https://jacobbuckman.com/2020-01-17-a-sober-look-at-bayesian-neural-networks/

本文为机器之心编译，转载请联系本公众号获得授权。

✄------------------------------------------------

加入机器之心（全职记者 / 实习生）：hr@jiqizhixin.com

投稿或寻求报道：content @jiqizhixin.com

广告 & 商务合作：bd@jiqizhixin.com