面向深度学习研究者的*概率分布*基础教程（附代码）

导读

本文介绍由Github用户graykode发布的概率分布基础教程，包括伯努利分布、高斯分布、狄利克雷分布等13种概率分布介绍与代码，主要针对用Python库进行深度学习研究的人员。

作者 | graykode

编译 | Xiaowen

深度学习中的概率分布关系一览

https://github.com/graykode/distribution-is-all-you-need

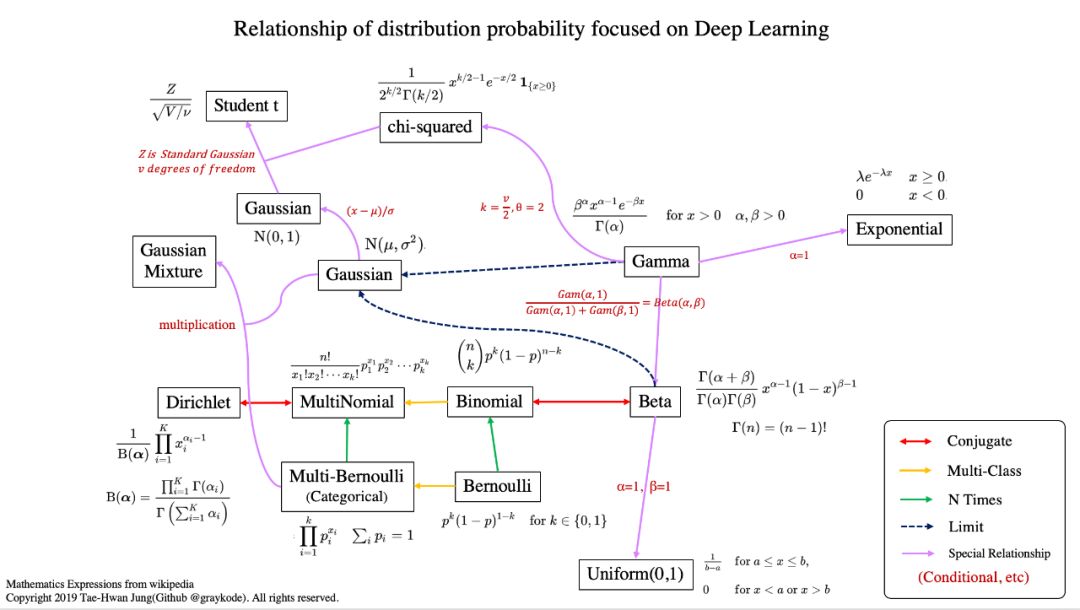
• conjugate 表示共轭分布关系

在贝叶斯概率理论中，如果后验分布p(n|x)与先验概率分布p(n)处于相同的概率分布家族中，则先验和后验被称为共轭分布，而在似然函数之前，先验被称为共 轭先验。

• Multi-Class 表示随机变量大于2
• N Times 表示我们还考虑先验概率P(X)
• 学习更多概率相关知识，推荐阅读[pattern recognition and machine learning, Bishop 2006]

分布概率与特征

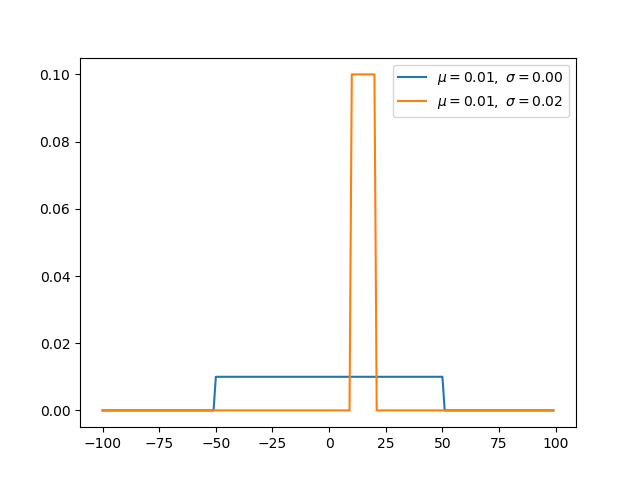
• 均匀分布（连续）
• 均匀分布在[a，b]上具有相同的概率值
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/uniform.py

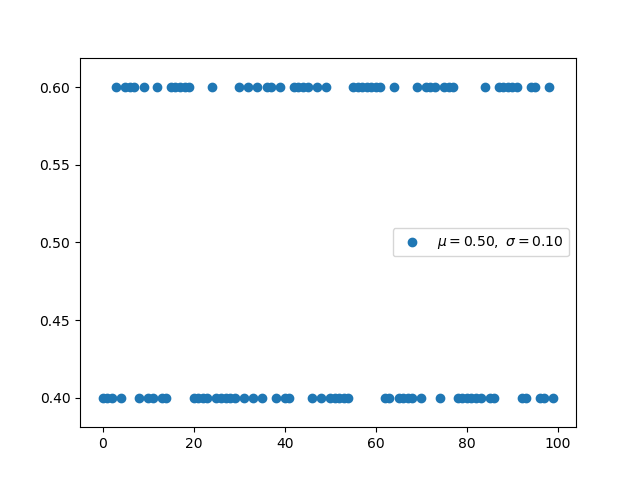
• 伯努利分布（离散）
• 不考虑先验概率p(x)的伯努利分布。因此，如果我们优化到最大似然，将容易过拟合
• 利用二值交叉熵对二值分类进行分类。它的形式类似于取伯努利分布的负对数
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/bernoulli.py

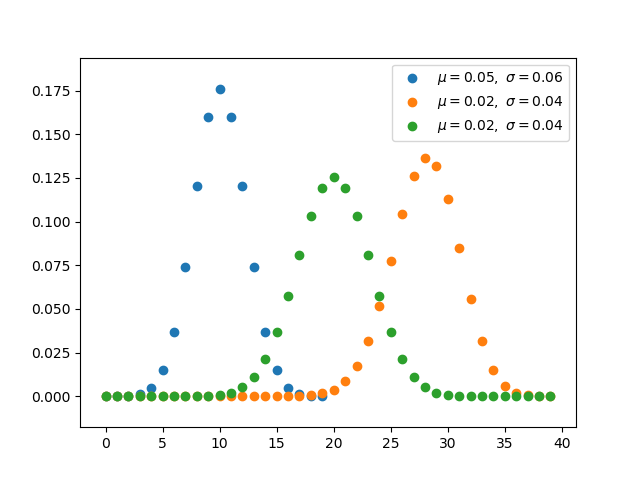
• 二项分布（离散）
• 参数n和p的二项分布是n个独立实验序列中成功次数的离散概率分布。
• 二项分布是通过指定预先选择的数目来考虑先验概率的分布
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/binomial.py

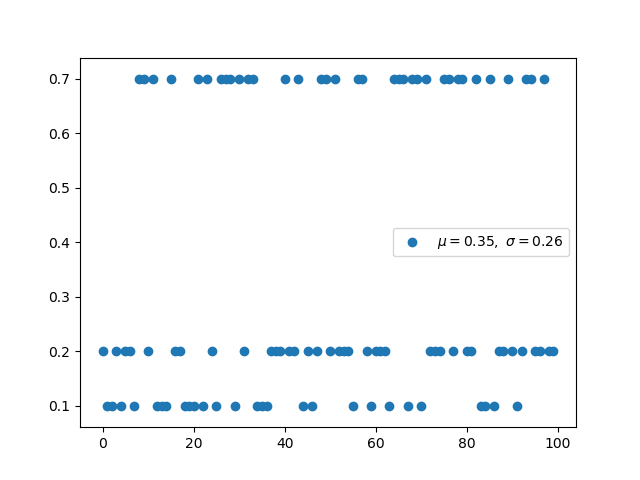
• Multi-伯努利分布，分类分布（离散）
• 多伯努利分布称为分类分布，是一个大于2的概率
• 交叉熵具有相同的形式，就像取多个伯努利分布的负对数
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/categorical.py

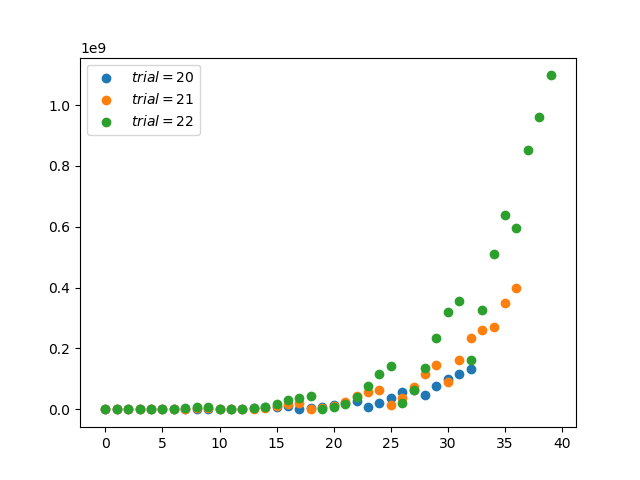
• 多项式分布（离散）
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/multinomial.py
  

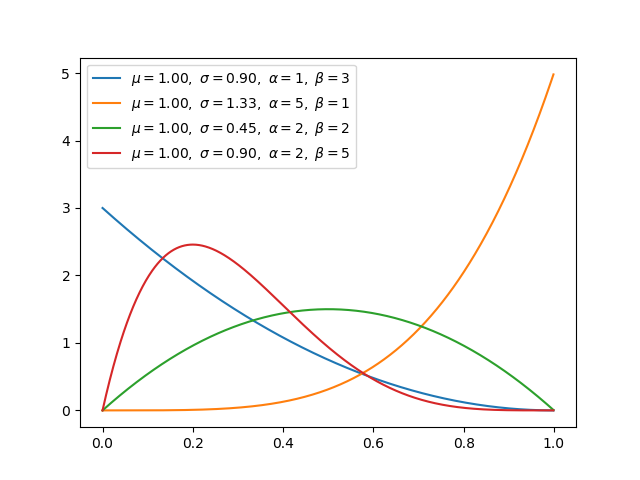
• Beta分布（连续）
• Beta分布与二项分布和伯努利分布是共轭的
• 利用共轭性，我们可以更容易地利用我们所知道的先验分布来获得后验分布
• 当Beta分布满足特殊情况（alpha=1，Beta=1）时，与均匀分布相同。
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/beta.py

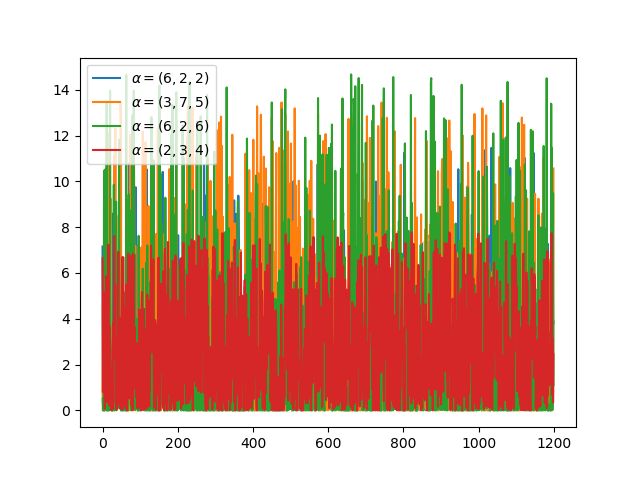
• 狄利克雷分布（连续）
• 狄利克雷分布与多项分布共轭
• 如果K=2，变为Beta分布
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/dirichlet.py

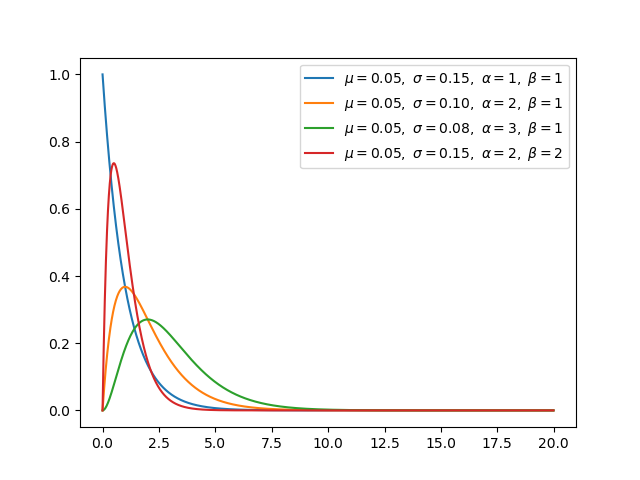
• Gamma分布（连续）
• 如果Gamma(a，1)/Gamma(a，1)+Gamma(b，1)与β(a，b)相同，则Gamma分布为β分布
•  指数分布和卡方分布是Gamma分布的特例
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/gamma.py

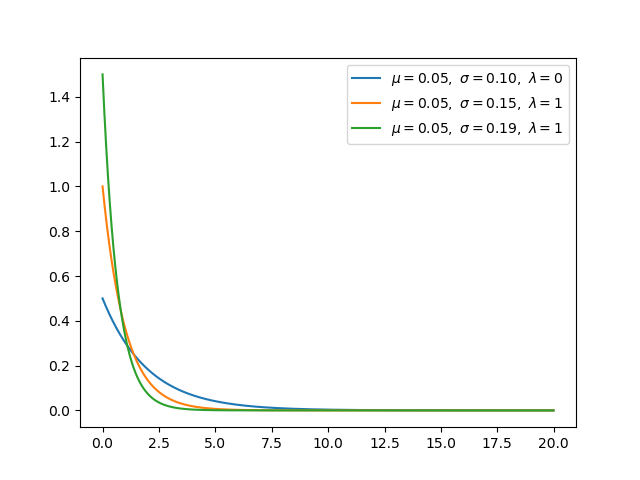
• 指数分布（连续）
• 指数分布是在Alpha为1时的Gamma分布的特殊情况
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/exponential.py

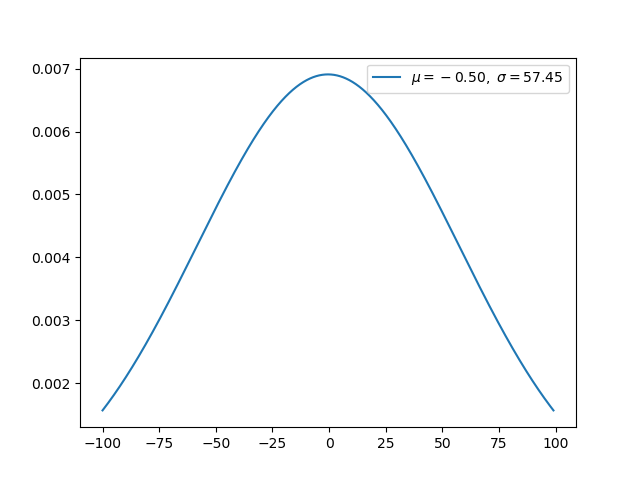
• 高斯分布（连续）
• 高斯分布是非常常用的连续值概率分布
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/gaussian.py

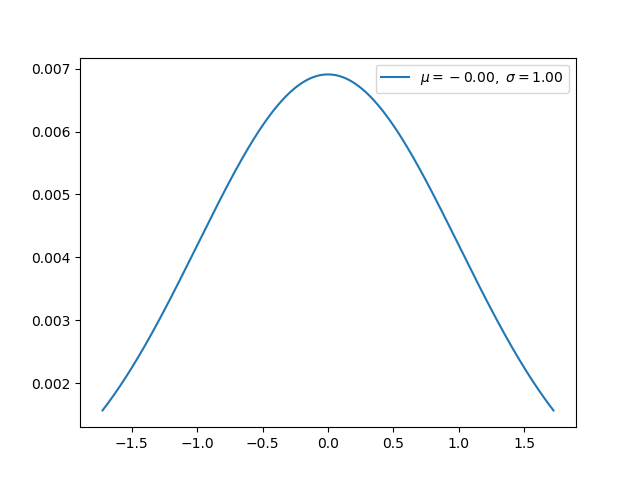
• 正态分布（连续）
• 正态分布是标准高斯分布，均值=0，方差=1
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/normal.py

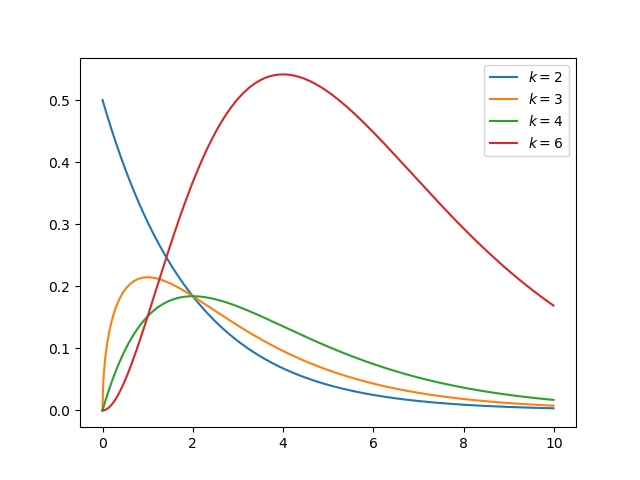
• 卡方分布（连续）
• 具有k自由度的卡方分布是k个独立标准正态随机变量平方和的分布
• 卡方分布是Beta分布的特例
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/chi-squared.py

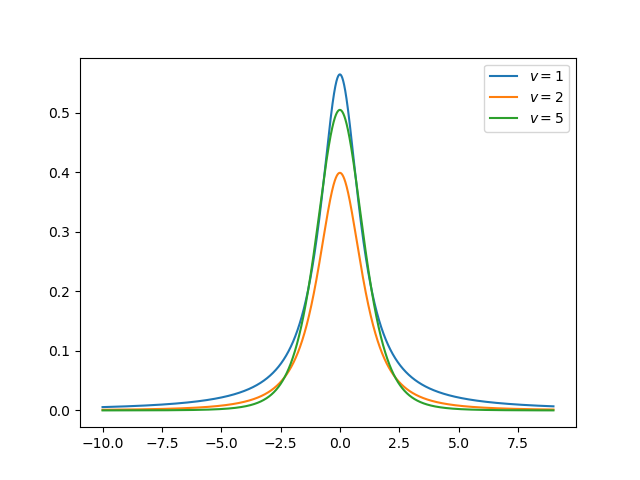
• Student-t 分布（连续）
• T型分布是对称的、钟形的，如正态分布，但具有较重的尾部，这意味着更容易产生远离其平均值的值
• 代码：https://github.com/graykode/distribution-is-all-you-need/blob/master/student-t.py

作者信息：

• Tae Hwan Jung @graykode, Kyung Hee Univ CE(Undergraduate).
• Author Email : nlkey2022@gmail.com

-END-

专 · 知

专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎登录www.zhuanzhi.ai，注册登录专知，获取更多AI知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程视频资料和与专家交流咨询！

请加专知小助手微信（扫一扫如下二维码添加），加入专知人工智能主题群，咨询技术商务合作~

专知《深度学习:算法到实战》课程全部完成！560+位同学在学习，现在报名，限时优惠！网易云课堂人工智能畅销榜首位！

点击“阅读原文”，了解报名专知《深度学习:算法到实战》课