用手机导致飞机失事，比遭雷劈概率还低

点击上方“腾讯科技”，选择“置顶公众号”

关键时刻，第一时间送达

来源 / 量子学派（ID：quantumschool）

内容经授权转载发布

一、飞机上关闭手机科学吗？

作为一个搞了近10年无线通信的老兵。

每次坐飞机被要求关手机时，心里总觉得这规定非常上古时代。

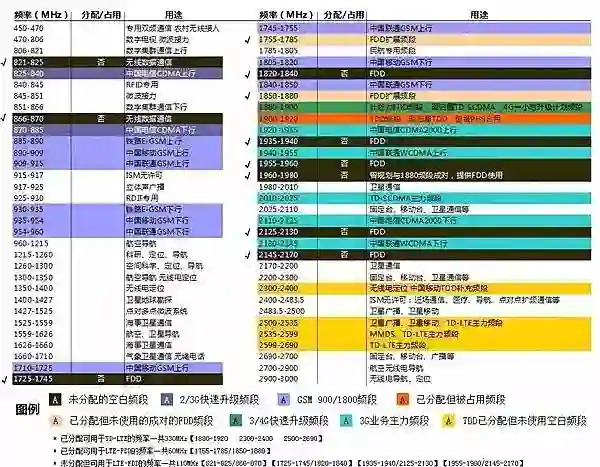
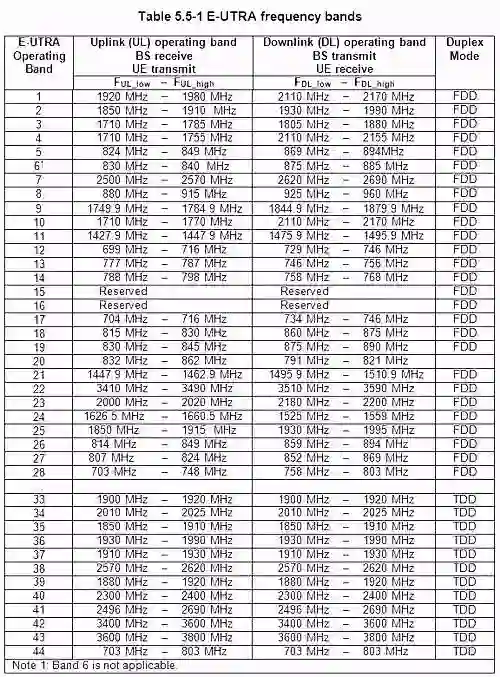
大部分人使用的手机是3G和4G信号（工作频率为3GHz和4GHz），完全不影响飞机通讯的vhf频率和vor信标。而飞机上不允许使用手机，是上世纪90年代欧美国家执行的，当时手机频率800MHz和900MHz，和机载设备的确有重叠！

但我仍然和大多数遵纪守法的中国公民一样，将手机关机然后阅读最讨厌的那份报纸，没有过于拒绝这种上古行为，因为处于开机状态的手机在起飞和降落阶段，搜索信号的频率和飞机与塔基联系的频率有相近区域，但信号强弱差太多，干扰基本不可能。

那么问题来了。

有人说，飞机和手机完全不在一个频率，相当于两个平行世界，怎么可能干扰？

这个很有道理。

又有人说有一种干扰叫杂散和交调，就像数学里的蝴蝶定理，怎么可能没干扰。

这个同样有道理。

有人说，难道中国的波音737和美国的波音737不一样，他们为什么可以玩手机。

马上有人反对，你看中国的航空安全指数这么高，不就是因为规定更严格吗？

…………

飞机上能不能玩手机这不是一个新命题，就像转基因一样，早被撕逼过多少次。

不管怎么说，从来没有哪一次航空事故被认定是因为手机通讯而造成的。一向保守的民航局飞标司敢出来说把决定权交给航空公司，当然也是因为有航空大数据的支持，谁不珍惜自己的乌纱帽。

所以仅仅从科学角度来说，这已经不是一个科学问题，而是一个心理学难题。

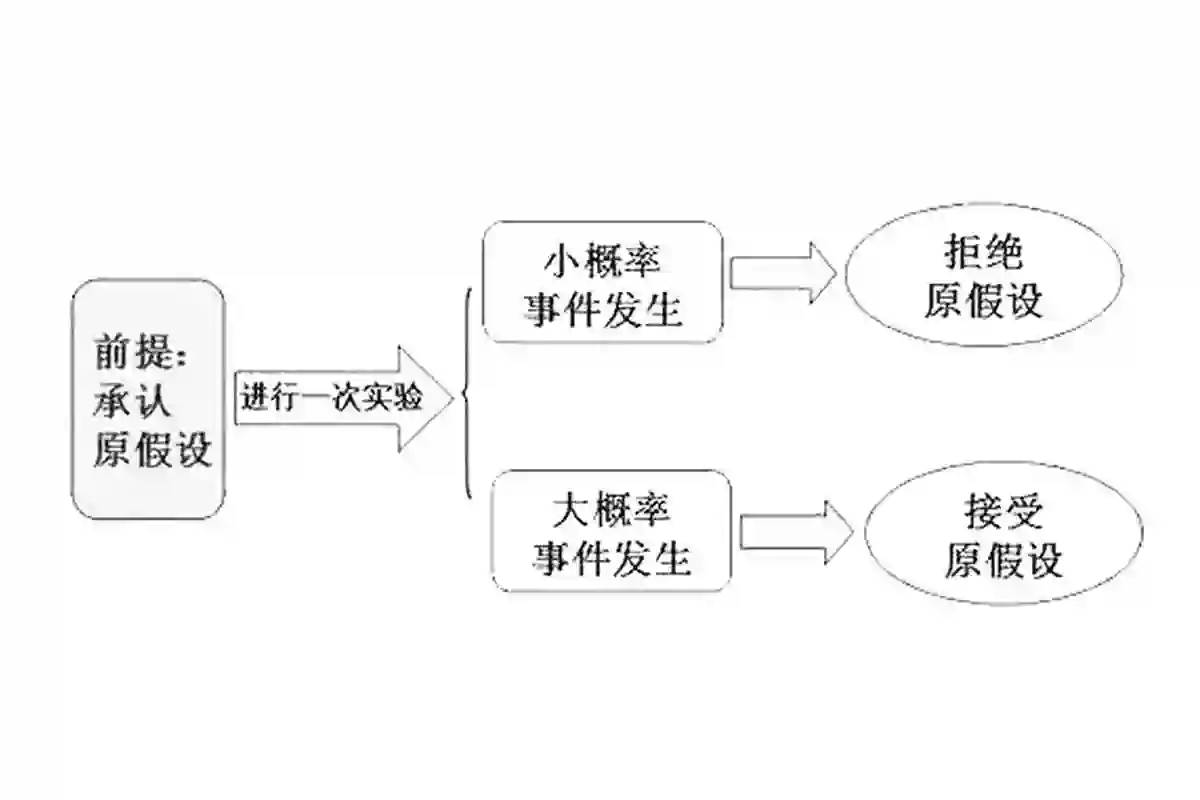
但当科学和心理学纠缠不清时，我们可以从另一个维度切入，将这个问题交给小概率原理，用概率论来反证这种规定的合理或者不合理。

二、将死亡概率分解的美国征兵文案

要讨论飞机上是否能玩手机的问题，首先要解决的是坐飞机是否安全的问题。

关手机这个动作不过是为了给自己一个心理暗示：嗯，这样安全多了。本质上是飞机的安全问题。

那为什么大家特别在意飞机上玩手机这件事，因为这直接涉及到自己生还是死，当它与你性命攸关时，很多时候你就不在意它的科学或者不科学了。

这与被征兵入伍的心态特别近似。

我们来看一则美国的征兵方案，它是如何通过概率来降低准士兵的死亡心理的：

来当兵吧！当兵其实并不可怕。

应征入伍后你无非有两种可能：有战争或者没有战争，没有战争有啥可怕的？

有战争后又有两种可能：上前线或者不上前线，不上前线有啥可怕的？

上前线后又有两种可能：受伤或者不受伤，不受伤又有啥可怕的？

受伤后又有两种可能：轻伤和重伤，轻伤有啥可怕的？

重伤后又有两种可能：可以治好和治不好，可治好有啥可怕的？

治不好更不可怕，因为你已经死了。

这个方案在美国家喻户晓、人人皆知。作为一个普通人，就算没有非常明确的具体数据，他也可以大概评估下风险指数。

有战争的可能性约为20%

打仗上前线的可能性约是25%

上前线受伤的可能性是20%

受伤后重伤的可能性约为20%

重伤后治不好的可能性是30%

根据概率乘法的一般定理，用条件概率的乘法公式计算，入伍上前线受重伤而死亡的概率仅为0.06%，毫无疑问这只是一个小概率事件，其发生的可能性微乎其微。

这则幽默又智慧的文案，是从隶属于科学的概率论出发，为大家陈述了一个朴素原理，当兵其实性价比挺高的。不得不说，对最坏结果的相当实事求是的风趣陈述，往往更易让人接受。

三、小概率原理，坐飞机有那么可怕吗？

我们回归到坐飞机是否安全的这个问题上，与战争不一样，战争的危险指数可以被Y纵向分解，而坐飞机的危险指数属于横向X指数，不容易被分解，但可以通过横向进行比较。我们从生活的危险概率来对比坐飞机的危险概率。

心脏病突然发作：（35岁以后）危险概率是1/77

在家中受伤：危险概率是1/80

受到致命武器的攻击：危险概率是1/260

死于心脏病：危险概率是1/340

家庭成员死于突发事件：危险概率是1/700

死于中风：危险概率是1/1700

乳腺癌（女性）：危险概率是1/2500

遭到强奸（女性）：危险概率是1/2500

死于突发事件：危险概率是1/2900

死于火灾：危险概率是1/5000

溺水而死：危险概率是1/5000

死于车祸：危险概率是1/5000

染上艾滋病：危险概率是1/5700

被谋杀：危险概率是1/11000

死于怀孕或生产（女性）：危险概率是1/14000

自杀：危险概率分别是1/20000（女性）和1/5000（男性）

那飞机的危险概率是多少：按每百万次飞行发生的有人员死亡的空难事故次数计算，1991年是1.7次，1999年首次降到1次以下，2000年再次下降到0.85次。按2000年的概率算，也就是117.65万次飞行才发生一次死亡性空难。按照2013年概率算，也就是310.21万次飞行发生一次死亡性空难。换句话说，如果有人每天坐一次飞机，要7223年才遇上一次空难。

从这个小概率来看，坐飞机可能只是比“喝水可能会噎死，吃饭会撑死”的风险指数稍大，如果真中了这样的彩头，只能归结为死神来了。

所以有些专业人士说民航这么多年来，为了一个莫须有的安全隐患，不研究，不取证，不测试……禁止用手机连一个科学证据都拿不出来，居然靠道听途说或者莫须有来搪塞，这是一种懒政行为也不是完全没有道理。

我觉得在飞机看某某时报引发的暴戾指数比手机干扰要危险得多。

四、相信概率论，不怕被雷劈。

当然，有人会反驳，你上文不是说了手机信号在飞机起降时的确会干扰吗？这点你为什么不加上去。好吧，这里又涉及到概率论：

2001年，NASA实验所证明“一旦存在与飞机组件工作频率相同的杂波，就会对飞行系统造成干扰”，可是，信号干扰的影响概率非常的小，甚至比出门被雷劈的概率还要小。也就是说，到目前为止都没有十足的证据能支持“飞行过程中未关机的手机会对飞机安全造成威胁”这一说法。

而且这还是2001年的数据，时间到了2017年，现在通讯都数字化了，民用通讯设备这么小的功率要干扰飞机通讯难度很高，萤火之光想要与太阳争辉，其实不过是飞蛾扑火。这是原来模拟通讯遗留下来的问题，数字时代飞机上的设置信号已经与民用信号中间差了3个数量级。

很多时候是一种“不怕一万，只怕万一”的心态在主导，与我们见神就拜没有什么两样，反正拜了总没有错，但这样的思维不是科学思维。

这有点像为了禁止强奸率，晚上禁止市民出门。重点不在这里，重点在于整个社会的正常治理。要保证飞机的安全，而是整个航空体系的系统管理，这才是安全最大的保证。

五、关手机有什么不好，你有那么忙吗？

手机到底能不能翻身作主人，相信争论还会延续。

但作为一个经常坐飞机的人，虽然从专业层面我觉得这属于小概率，但还是建议不要解封的好。好不容易在飞机上休息下，你这一解封，领导马上安排任务。

还有，好不容易能安静几分钟，你这一解封飞机上肯定热闹，肯定有人扯着嗓子喊：“我在北京去纽约的路上，飞机上信号不好……”一想到这些我都会疯掉，幸好高空没有信号。

你有那么忙？能不能好好坐个飞机，俯瞰祖国的高山流水。