CS224W 7.1 Graph Representation Learning

自Deepwalk开始,图表示学习已经成为图挖掘领域最热门的方向之一. 现在火热的图神经网络可以说是图表示学习2.0

这里我们一起重温下经典的图表示学习算法.

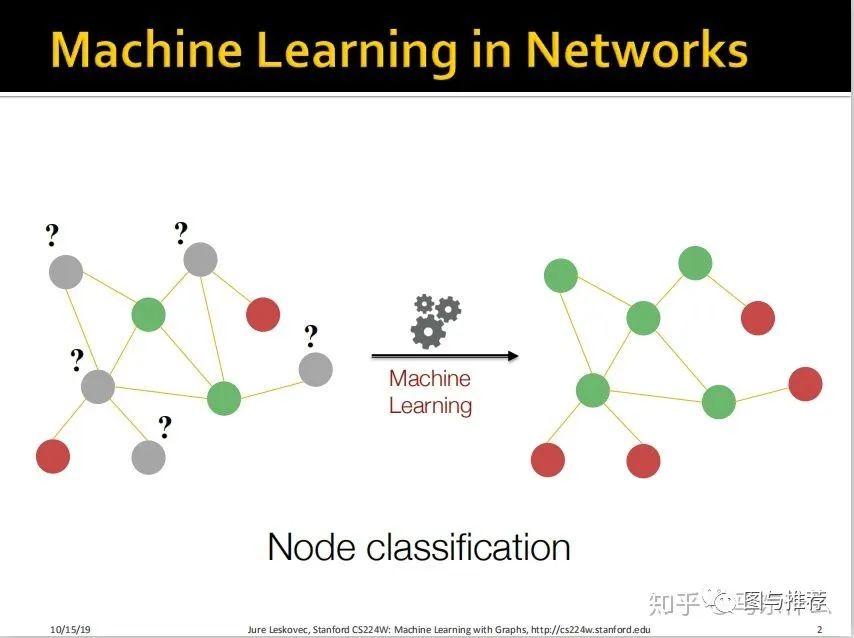
我们要解决的问题就是如何在已知部分标签的情况下，通过图数据本身的特点去预测无标签的样本；

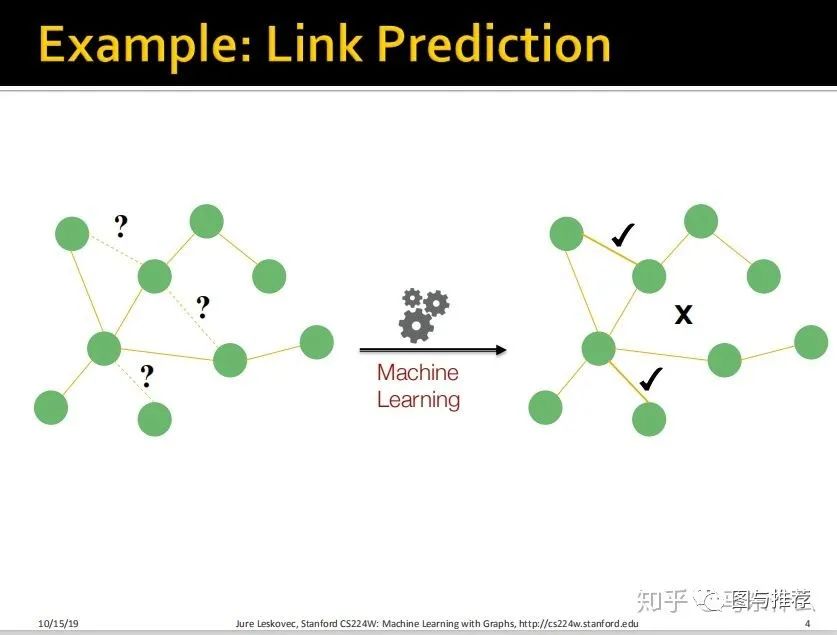
除此之外，还有一个典型的场景是我们需要去预测edge——这被称为link prediction。

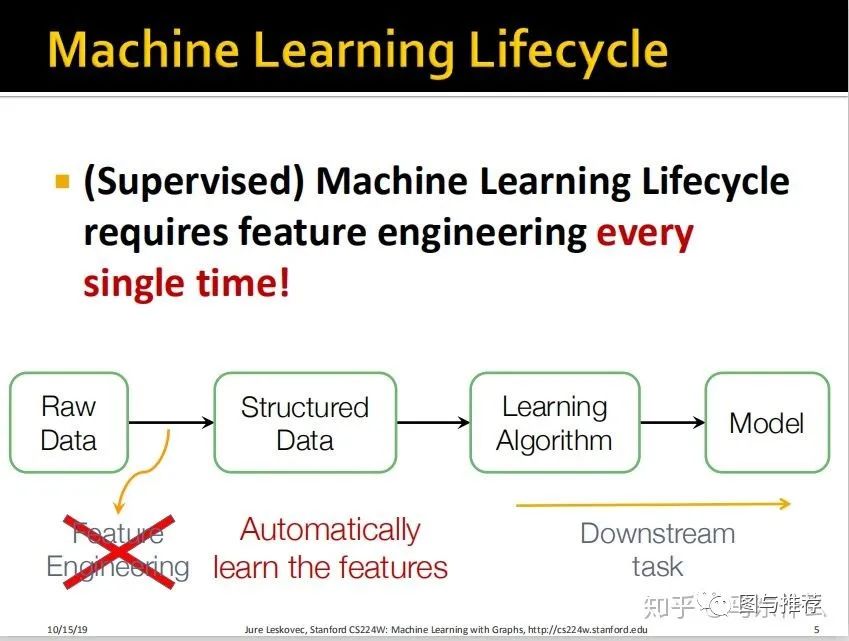
介绍了普通的有监督学习的流程，基本上都是讲烂的东西这里就不翻了，因为常规的feature engineering非常耗时耗力而且也不一定能够将原始数据中潜在的一些规律表示出来，所以希望借助神经网络来自动抽取潜在的特征并且以特征矩阵的形式展现。

这里把针对分类、回归、聚类等不同目标的模型训练与应用称之为 下游任务，而特征工程则属于上游任务。

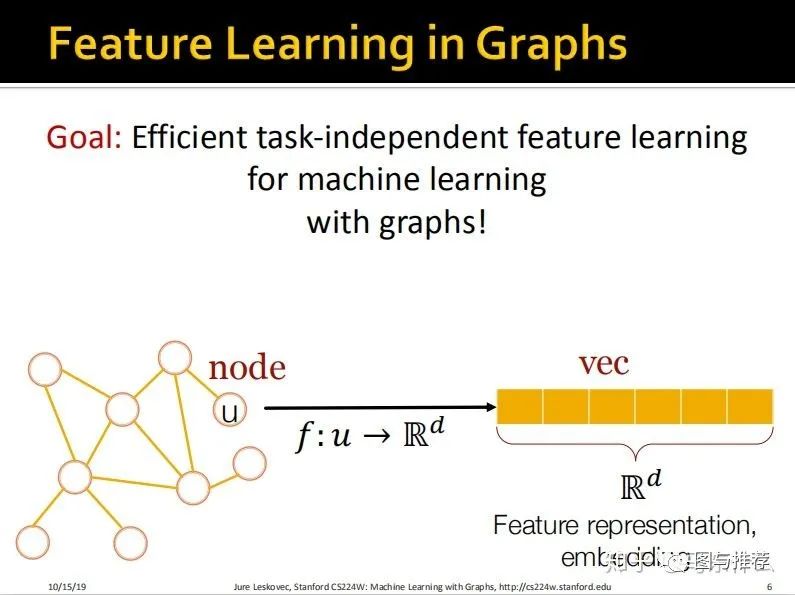
目标：我们希望图数据的特征工程能够作为独立的上游任务进行，通过一些方法在特征工程阶段对特征进行抽取，然后将得到的最终的特征矩阵用于下游的各种任务，比如使用gbdt分类、kmeans进行聚类分析等等。

具体的形式就是将每一个节点表示成一个d维的向量；

如果熟悉word2cec的其实对这种思路应该是非常熟悉的，这和文本中将没有给单词embedding成一个词向量几乎是一样的思路。

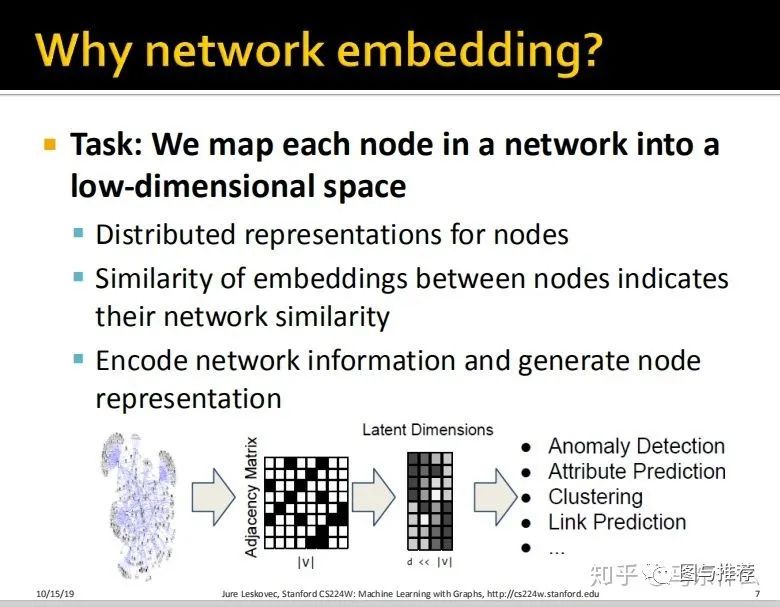
说老实话，这一段的描述和文本的发展历程是非常相似的，文本早期最简单也最麻烦的是词袋模型，而图数据对应的简单而麻烦的是adjacency matrix——即领接矩阵：baike.baidu.com/item/%E

词袋和邻接矩阵都有类似的问题：

1、高维稀疏，这对于gbdt或者是knn、kmeans之类的算法来说是非常麻烦gbdt太容易过拟合，knn这类base on 距离计算的算法受到高维诅咒的问题影响效果很差；

2、丢失了空间结构的信息，词袋丢失了上下文的关系信息，邻接矩阵丢失了二度、三度。。等结构信息，实际上是一种损失信息的特征转换的方式；

3、etc；

而对于embedding的方式二者也是非常类似的，文本有矩阵分解、lsi、lda这类的向量化方法，也有word2vec这类基于神经网络结构的embedding方式，以及自编码器这样的自监督的方式，而图也有node2vec这类基于统计方法的embedding方式，基于gnn的embedidng方式以及graph 自编码器这样的方式。可以说，对照文本来类比学习，很多图上的概念就能很好的切身体会；

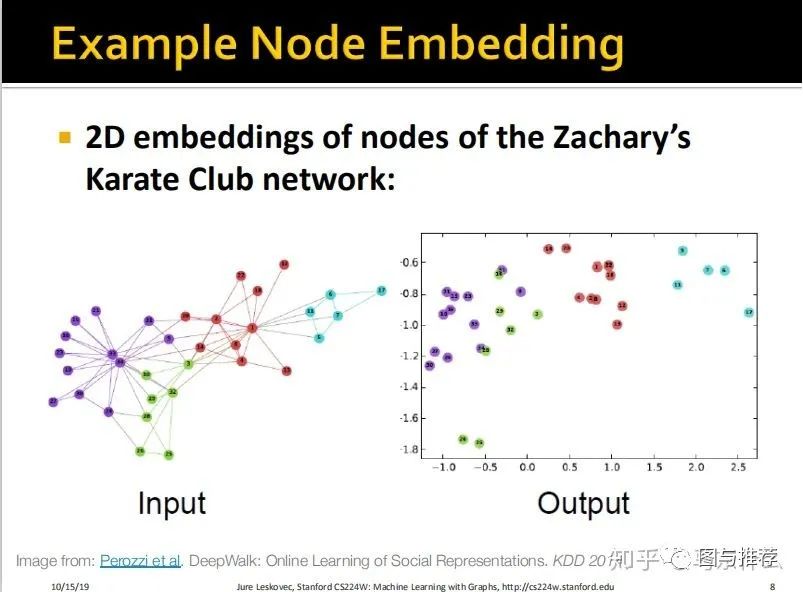
是不是很类似于：

word2vec之后的二维可视化的图？

我们平常熟悉的CNN和RNN可以处理的数据，这里统称为“grid”网格结构，如上图所示，例如一张图片中的每一个像素点都是一个节点，一段语音波形也可以表示成一个一维的有序列关系的节点，

这里实际上是把图像、音频（其实也有包括文本和传统的tabular数据）都当作了图数据的一种。

对于无序的tabular数据，即没有图像的规律的空间结构（比如某一个局部是一个鼻子，那么这些鼻子上的像素点相互之间是有空间关联关系的；比如一段有顺序的文本中，单词是有先后顺序关系的，而tabular数据就是一个一个完全独立的节点，不同的节点（样本）之间是没有任何关联的，而每一个样本的特征就是节点对应的属性（property））

然而：

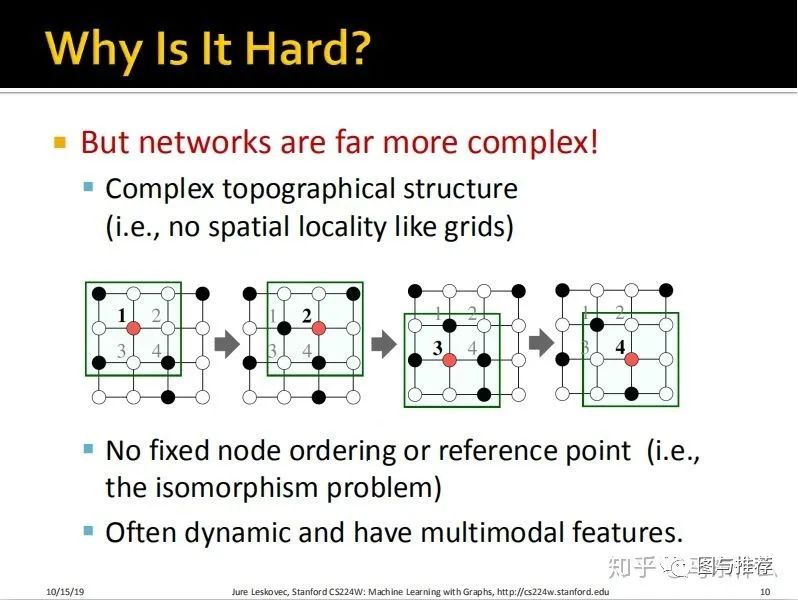
实际中，我们遇到的问题更加复杂：

1、不像grid数据那样有规律性；

2、没有固定的节点顺序或者参考点（一个典型的图数据结构对齐进行左右、上下翻转等不会改变图数据本身的含义）

3、 图数据常常是动态（例如节点不是固定的，可能会随着时间消失或出现，比如新的社交关系的生成，而对于图像、文本和表格数据，这些是相对固定）的并且具有多模态特征（例如edge可以代表节点之间的社交关系，也可以代表节点之间的主次关系）。

现在我们假设一个简单的场景，我们有一个图G，V是G的顶点集，A是G的领接矩阵的表示，假设是一个binary的邻接矩阵（也就是节点之间是一度关系，不考虑更复杂的多度关系的情况）并且我们不考虑节点的属性（特征矩阵）或者是其它的额外的信息。

当然也有将节点属性考虑进去的embedding方法，但是这节课不做介绍。

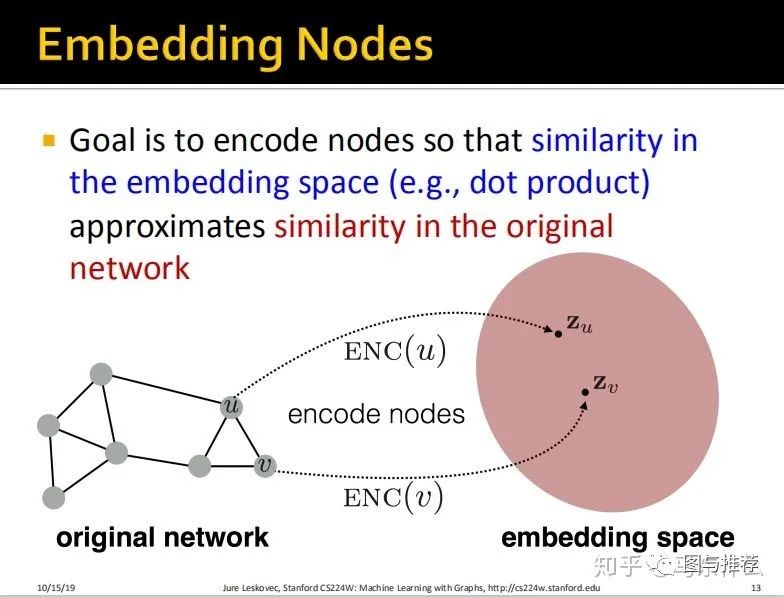
我们的目标就是将所有节点都映射到一个新的特征空间，并且在原始的图结构上相近的节点，在新的特征空间中也是具有强相似性的（和word2vec的思路是一样的）；

但是这个时候就有一个比较重要的地方了，我们要使得原始图结构中，节点之间的相似性度量的结果和embedding之后的节点之间的相似度度量的结构是接近的（这里对于embedding之后的特征空间的相似性度量方式定义如下图，就是简单的dot product 点积）

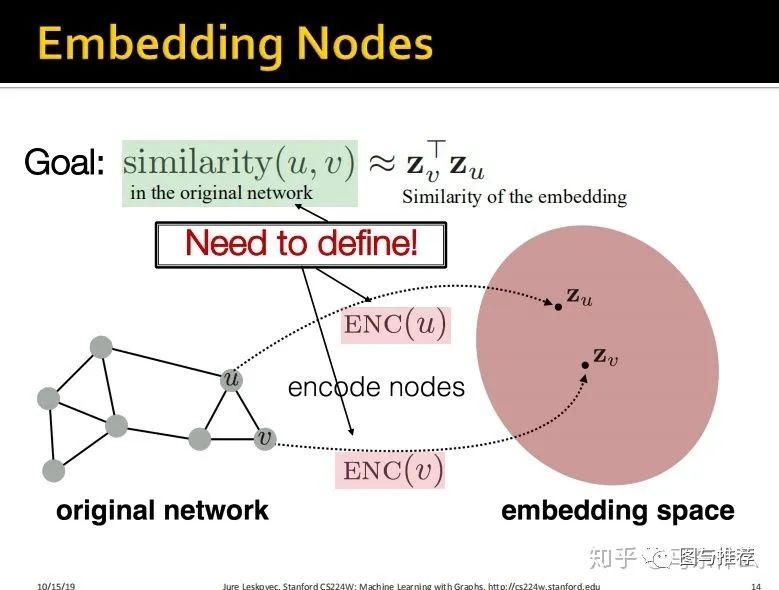
这里给的相似性定义的例子如上，就是两个向量的dot product（点积）。

这里给node embedding的思路如上：

1、首先我们要定义一个encoder，也就是node 到 embedding的编码器（映射函数）；

2、然后我们要定义相似性函数（例如，在原始的图结构上的相似性的度量函数）

3、优化encoder的参数使得节点在原始的图结构和embedding空间中的相似度接近，说白了就是A和B在embedding前是靠近的，A和B在embedding之后还得是靠近的。

所以这里就有两个需要解决的问题：

1、encoder如何定义；

2、原始的图结构中的similarity function如何定义（embedding空间的similarity直接使用dot product定义，当然这只是一种最长使用的embedding空间的similarity的定义方式，我们可以根据自己的需要去定义别的度量方式，不过这里没深入介绍了）；

（学生问题，我们前面仅仅是针对相似节点embedding之后也要相似的问题进行优化，那么如果原始的图结构里两个不相似的节点在embedding之后却相似了该怎么办？答案是在我们的优化目标中加入不同节点之间的相似性度量，这样模型能够同时优化“相同节点相似”和“不同节点不相似" 两个目标，后面会详细介绍）

现在进入第一个问题，encoder如何定义，首先介绍了最简单的一种encoder的方法：

浅层编码，如下图：

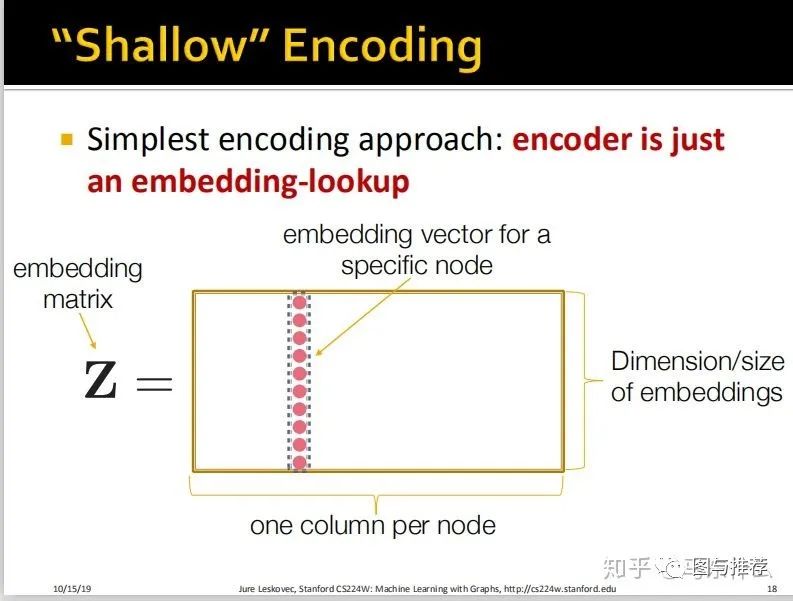
这实际上和nlp里的embedding的形式是几乎一样的；

对所有节点做onehot展开，然后通过lookup的方式来查询每一个node在node embedding 矩阵中其对应的embedding向量；

常见的这类shallow浅层的embedding方法有：

（node2vec是deepwalk的一种扩展方法，以及一种知识图谱嵌入的方法TransE。

我们选择哪一种embedding的方法取决于我们如何在原始的图结构中定义相似性，是互相连接的节点具有相似性？还是具有相同的邻居的节点具有相似性？还是具有相同结构作用的节点具有相似性？等等，这部分的定义取决于你要解决的问题的形式。比如说如果在反欺诈的场景中，欺诈分子之间的connect特别强，典型的团伙作案模式，那么我们就把similairy定义为connected similarity。

不同的相似性定义决定了我们如何去选择不同的embedding的方法。

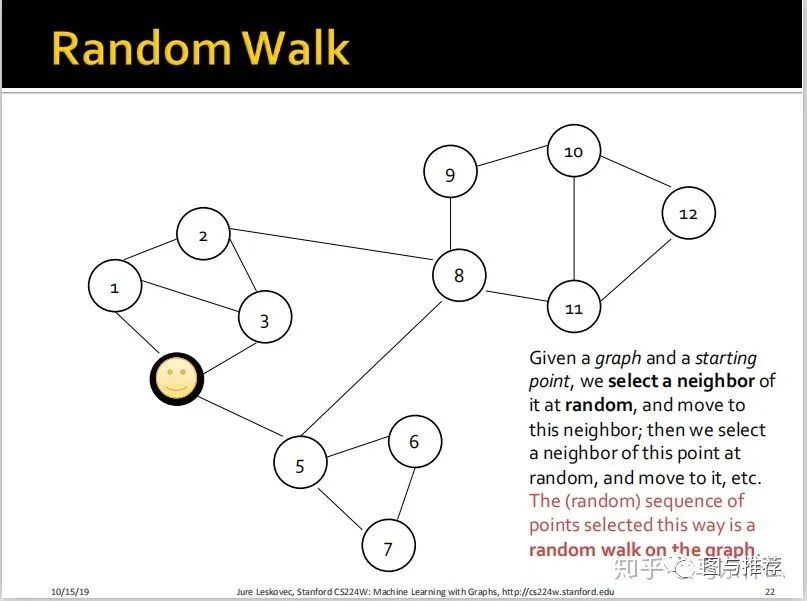
首先是random walk的定义；

给定一个图G和一个起点A，我们随机选择A的一个邻节点B，并且移动到这个邻节点B，然后我们在点B上再随机选择一个B的邻节点C，然后移动到这个邻节点C，依此类推。这样，我们最终得到的一个随机的序列A—>B—>C—>。。。。即为图G上的一个随机游走产生的序列。

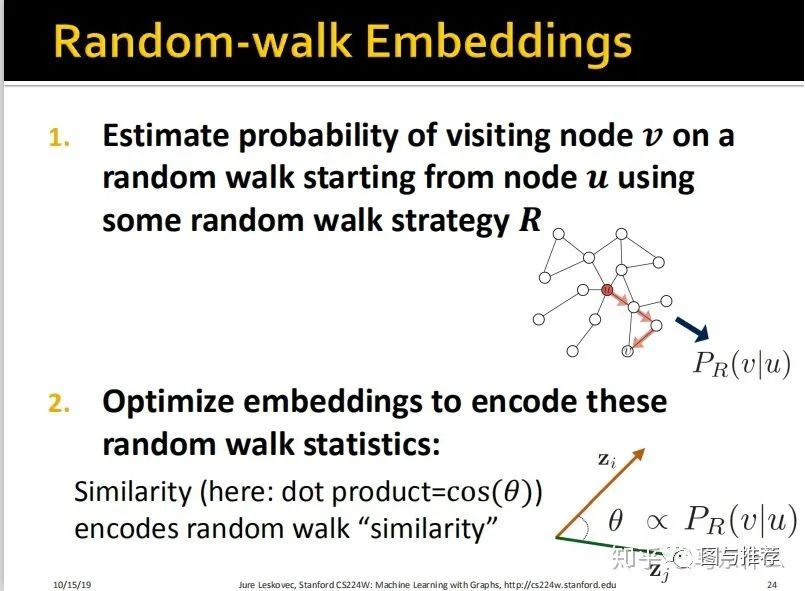
1、使用某种随机游走策略R估计从节点u开始的随机游走过程中访问到节点v的概率；

2、优化embedding矩阵以将random walk的统计信息encode进来。

为什么要使用random walk的策略？

1、强大的表达能力：通过随机游走的方式灵活的定义了节点的相似性，充分考虑了本地和高阶的邻域信息；

2、 高效：训练时不需要考虑所有节点对；只需要考虑在随机游走中”共现“的节点对；

可以看到random walk的过程中没有应用到任何的标签，属于一种无监督的特征学习的方法（个人感觉用自监督的representation learning描述更合适。。）

直觉：找到一个d维的embedding的空间，这个空间中可以保持原始的图结构中的节点之间的相似性；

方法：学习node embedding使得在原始的图结构中靠近的节点在互相接近；

那么给定一个节点u，我们如何来定义其邻域的节点们呢？

方法是通过某种策略R来得到u的邻节点的一些特定的信息Nr（u）；

（学生问，如果一个节点其邻节点的数量非常大，random walk的效率是不是就会降低很多，答案是，对的，因此不会使用一个节点的所有邻节点进行random walk而会采取一些优化措施，例如像word2vec一样定义一个windows，只取一部分上下文进行word embedding的训练）

下面开始正式进入算法原理讲解环节：

给定图G=(V,E)，我们的目标是学习到一个映射函数Z，可以将u映射到一个d维空间；

我们的目标函数就是最大化对数似然函数；

看到这里可能会有点懵，没事儿，继续往下看，后面会给出详细的解释和具体的例子。

random walk优化的流程：

1、在一个完整的图上，我们使用某个策略R为每一个node跑一个固定长度的短的random walk；

2、为每一个node——u，保存以u为starting node的random walk产生的序列数据；

3、根据最大对数似然函数对embedding进行参数更新；

看的时候比较懵逼，找到了一些大佬的笔记是2014年的关于deep walk的论文，然后才看明白了。

rhaegar：生动详解deepwalk算法（graph embedding） zhuanlan.zhihu.com浅梦：【Graph Embedding】DeepWalk：算法原理，实现和应用 zhuanlan.zhihu.com

这里所说的deepwalk就是我们前面说的通过 random walk来对节点embedding。

思路看起来非常简单自然，

DeepWalk的思想类似word2vec，使用 图中节点与节点的共现关系来学习节点的向量表示。那么关键的问题就是如何来描述节点与节点的共现关系，DeepWalk给出的方法是使用随机游走(RandomWalk)的方式在图中进行节点采样。

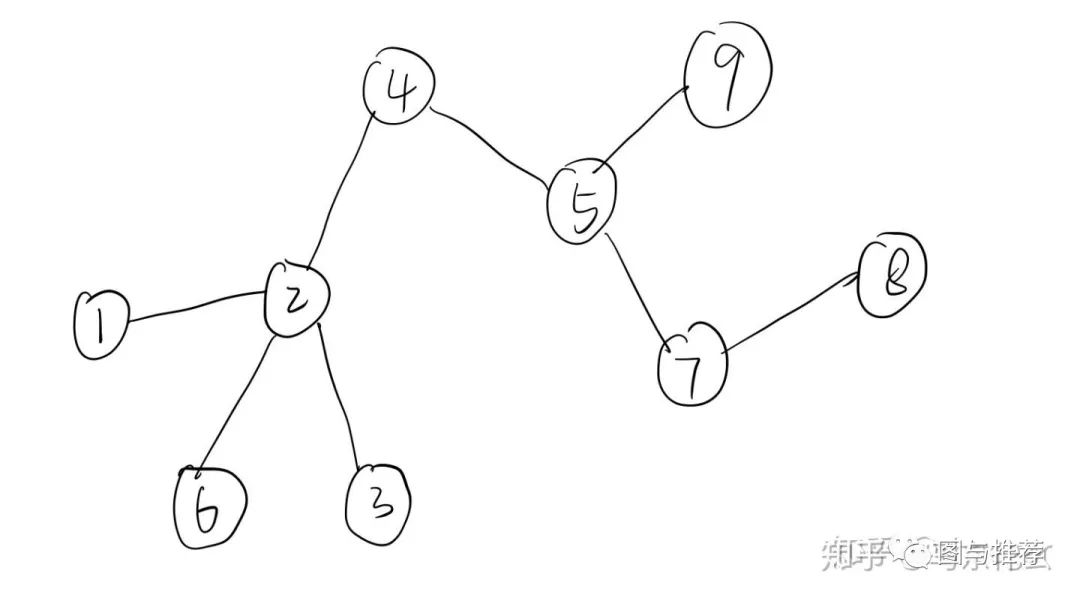
例如这是一个完整的网络图，如果我们以节点3为starting point，进行一次固定长度为3的短序列，那么我们可以得到:

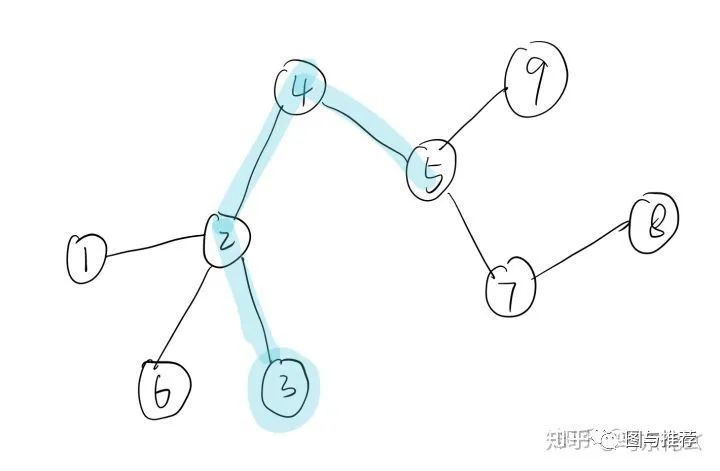
然后开始借鉴NLP思想，这条路径上临近点与点之间必然联系密切 有共同特征。现在将3-2-4-5当作一个句子，各个顶点为句子中单词

这样，3-2-4-5就是word2vec中的一个句子，3，2，4，5分别对应的是一个单词。

然后就是word2vec的求解过程了。。。。

---

这样，后面猝不及防的公式就都迎刃而解了：

对比一下word2vec的损失函数：

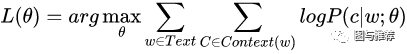
经过softmax之后：

简直和ppt上的公式一毛一样

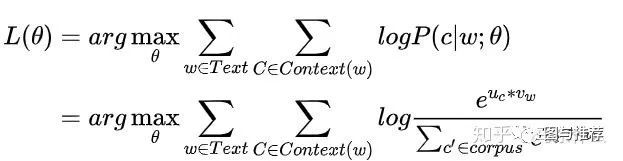
这里我们对word2vec的损失函数取负数转换为极小化问题，其形式就非常相似了，V代表所有random walk出来的序列，Nr（u）代表了以u为start point而random walk出来的一条序列，v代表了这条序列上的与u”共现“的所有的节点；

显然，random walk出来的序列u对应了text里的每个句子w，而u里的每个节点v就是句子中的每个词语C。w；θ 对应的就是Zu的变换关系。

自然而然的，在早期版本的word2vec中我们使用的是softmax来处理P，softmax函数后面对应的输出是所有单词，这里也是一样，使用softmax，输出对应的是所有节点。

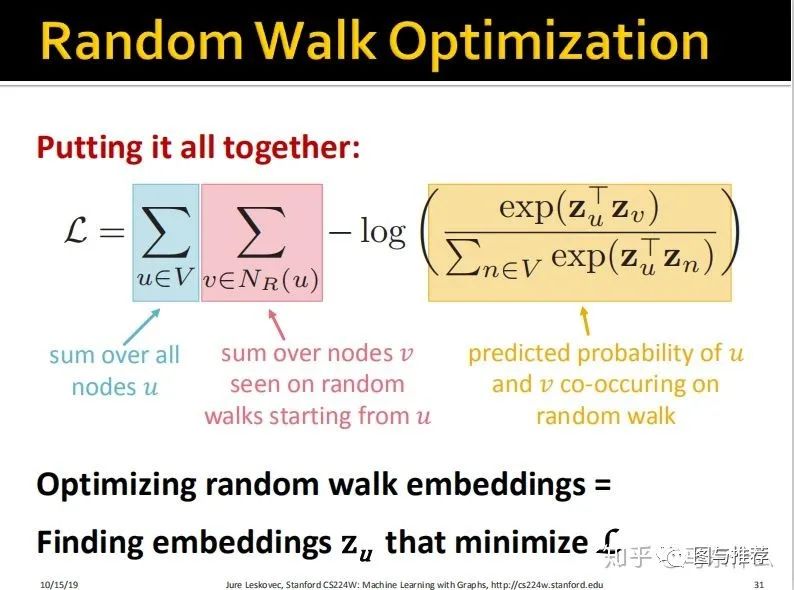
那么，如果熟悉word2vec，那么接下来的一切就很顺畅了，上面的问题早期的word2vec也面临着一样的问题，因为我们的softmax后面借的是所有的词或者所有的节点，所以无论是前向和反向都要算到死，因此后来的大佬们想出了一些替代的，近似的方法。一个是把softmax变成分层softmax，通过霍夫曼树的方式来构建，关于技术细节，后续整理representation learning的时候再讨论吧。另一个更常见的方式是使用negtive samplin。

（上面绿色的部分对应的论文介绍了为什么这种近似的方法是有效的）

另外主要注意两点，k越大则对于embedding的计算越鲁棒然而越大的k也意味着对于少数样本的估计偏差越大（因为一个node所在random walk序列的与其共现的节点数量相对于全部节点来说是很稀少的，所以我们仅仅在不与其共现的节点中抽取一部分出来参与embedding的训练）。

这里的negtive sampling的概念和word2vec里的是一样的，所以就不详细介绍了。

需要注意的是，这里的negtive sampling和我们在不均衡学习中所说的负采样不一样，（当然二者都能缓解不均衡问题）我们在unbalanced learning中提到的负采样使用的均匀采样，而word2vec和deepwalk的负采样都是根据词或者节点出现的频率来采样的，简单说，出现的频率越大其被采样到的次数越多，否则越少，关于negtive sampling以及另外一种 分层softmax，这一节课没有详细介绍，感兴趣的百度即可，挺多人讨论过这两种优化方法的了。

那么，我们应该怎么random walk？

实际上前面的deepwalk就是一种比较多见的思路了，就是每一个节点走随机random walk。。。

然而，这种方式定义的相似性太过局限。

1、deepwalk无法应用于有权图，因为使用word2vec的思路是没有考虑边的概念的，因为词与词之间也没有所谓边的概念（补充）；

2、更重要的是，我们前面说过如何定义原始的图数据上 的相似性的问题：

显然，deepwalk的方法只能定义 connected和neighbor的相似性，也就是只能捕捉到node和node之间相互连接以及share the same nodes这种相似性；但是假设有两个节点node a和node b，其graph structure是一摸一样的，但是二者的距离很远，显然deepwalk是无法捕捉到这种相似性的。具体的例子后面的ppt有详细介绍