【斯坦福谷歌】最新《图机器学习》综述论文，38页pdf阐述最新图表示学习进展

近年来，人们对学习图结构数据表示的兴趣大增。基于标记数据的可用性，图表示学习方法一般分为三大类。第一种是网络嵌入(如浅层图嵌入或图自动编码器)，它侧重于学习关系结构的无监督表示。第二种是图正则化神经网络，它利用图来增加半监督学习的正则化目标的神经网络损失。第三种是图神经网络，目的是学习具有任意结构的离散拓扑上的可微函数。然而，尽管这些领域很受欢迎，但在统一这三种范式方面的工作却少得惊人。在这里，我们的目标是弥合图神经网络、网络嵌入和图正则化模型之间的差距。我们提出了图结构数据表示学习方法的一个综合分类，旨在统一几个不同的工作主体。具体来说，我们提出了一个图编码解码器模型(GRAPHEDM)，它将目前流行的图半监督学习算法(如GraphSage、Graph Convolutional Networks、Graph Attention Networks)和图表示的非监督学习(如DeepWalk、node2vec等)归纳为一个统一的方法。为了说明这种方法的一般性，我们将30多个现有方法放入这个框架中。我们相信，这种统一的观点既为理解这些方法背后的直觉提供了坚实的基础，也使该领域的未来研究成为可能。

概述

学习复杂结构化数据的表示是一项具有挑战性的任务。在过去的十年中，针对特定类型的结构化数据开发了许多成功的模型，包括定义在离散欧几里德域上的数据。例如，序列数据，如文本或视频，可以通过递归神经网络建模，它可以捕捉序列信息，产生高效的表示，如机器翻译和语音识别任务。还有卷积神经网络(convolutional neural networks, CNNs)，它根据移位不变性等结构先验参数化神经网络，在图像分类或语音识别等模式识别任务中取得了前所未有的表现。这些主要的成功仅限于具有简单关系结构的特定类型的数据(例如，顺序数据或遵循规则模式的数据)。

在许多设置中，数据几乎不是规则的: 通常会出现复杂的关系结构，从该结构中提取信息是理解对象之间如何交互的关键。图是一种通用的数据结构，它可以表示复杂的关系数据(由节点和边组成)，并出现在多个领域，如社交网络、计算化学[41]、生物学[105]、推荐系统[64]、半监督学习[39]等。对于图结构的数据来说，将CNNs泛化为图并非易事，定义具有强结构先验的网络是一项挑战，因为结构可以是任意的，并且可以在不同的图甚至同一图中的不同节点之间发生显著变化。特别是，像卷积这样的操作不能直接应用于不规则的图域。例如，在图像中，每个像素具有相同的邻域结构，允许在图像中的多个位置应用相同的过滤器权重。然而，在图中，我们不能定义节点的顺序，因为每个节点可能具有不同的邻域结构(图1)。此外，欧几里德卷积强烈依赖于几何先验(如移位不变性)，这些先验不能推广到非欧几里德域(如平移可能甚至不能在非欧几里德域上定义)。

这些挑战导致了几何深度学习(GDL)研究的发展，旨在将深度学习技术应用于非欧几里德数据。特别是，考虑到图在现实世界应用中的广泛流行，人们对将机器学习方法应用于图结构数据的兴趣激增。其中，图表示学习(GRL)方法旨在学习图结构数据的低维连续向量表示，也称为嵌入。

广义上讲，GRL可以分为两类学习问题，非监督GRL和监督(或半监督)GRL。第一个系列的目标是学习保持输入图结构的低维欧几里德表示。第二系列也学习低维欧几里德表示，但为一个特定的下游预测任务，如节点或图分类。与非监督设置不同，在非监督设置中输入通常是图结构，监督设置中的输入通常由图上定义的不同信号组成，通常称为节点特征。此外，底层的离散图域可以是固定的，这是直推学习设置(例如，预测一个大型社交网络中的用户属性)，但也可以在归纳性学习设置中发生变化(例如，预测分子属性，其中每个分子都是一个图)。最后，请注意，虽然大多数有监督和无监督的方法学习欧几里德向量空间中的表示，最近有兴趣的非欧几里德表示学习，其目的是学习非欧几里德嵌入空间，如双曲空间或球面空间。这项工作的主要动机是使用一个连续的嵌入空间，它类似于它试图嵌入的输入数据的底层离散结构(例如，双曲空间是树的连续版本[99])。

鉴于图表示学习领域的发展速度令人印象深刻，我们认为在一个统一的、可理解的框架中总结和描述所有方法是很重要的。本次综述的目的是为图结构数据的表示学习方法提供一个统一的视图，以便更好地理解在深度学习模型中利用图结构的不同方法。

目前已有大量的图表示学习综述。首先，有一些研究覆盖了浅层网络嵌入和自动编码技术，我们参考[18,24,46,51,122]这些方法的详细概述。其次，Bronstein等人的[15]也给出了非欧几里德数据(如图或流形)的深度学习模型的广泛概述。第三，最近的一些研究[8,116,124,126]涵盖了将深度学习应用到图数据的方法，包括图数据神经网络。这些调查大多集中在图形表示学习的一个特定子领域，而没有在每个子领域之间建立联系。

在这项工作中，我们扩展了Hamilton等人提出的编码-解码器框架，并介绍了一个通用的框架，图编码解码器模型(GRAPHEDM)，它允许我们将现有的工作分为四大类: (i)浅嵌入方法，(ii)自动编码方法，(iii) 图正则化方法，和(iv) 图神经网络(GNNs)。此外，我们还介绍了一个图卷积框架(GCF)，专门用于描述基于卷积的GNN，该框架在广泛的应用中实现了最先进的性能。这使我们能够分析和比较各种GNN，从在Graph Fourier域中操作的方法到将self-attention作为邻域聚合函数的方法[111]。我们希望这种近期工作的统一形式将帮助读者深入了解图的各种学习方法，从而推断出相似性、差异性，并指出潜在的扩展和限制。尽管如此，我们对前几次综述的贡献有三个方面

• 我们介绍了一个通用的框架，即GRAPHEDM，来描述一系列广泛的有监督和无监督的方法，这些方法对图形结构数据进行操作，即浅层嵌入方法、图形正则化方法、图形自动编码方法和图形神经网络。

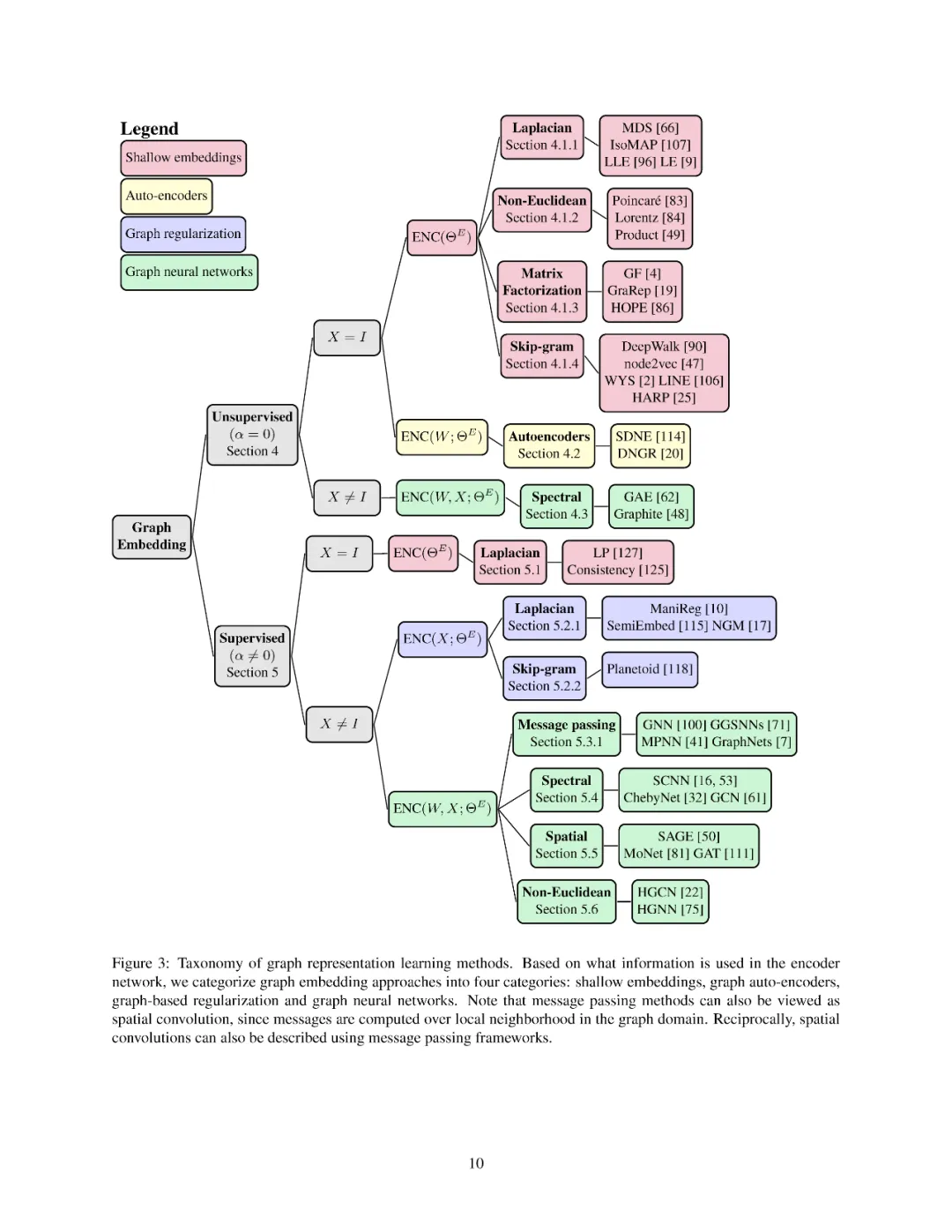
• 我们的综述是第一次尝试从同一角度统一和查看这些不同的工作线，我们提供了一个通用分类(图3)来理解这些方法之间的差异和相似之处。特别是，这种分类封装了30多个现有的GRL方法。在一个全面的分类中描述这些方法，可以让我们了解这些方法究竟有何不同。

• 我们为GRL发布了一个开源库，其中包括最先进的GRL方法和重要的图形应用程序，包括节点分类和链接预测。我们的实现可以在https://github.com/google/gcnn-survey-paper上找到。