积分梯度：一种归因分析方法

↑ 点击 蓝字  关注极市平台

作者丨科技猛兽

编辑丨极市平台

极市导读

 

积分梯度 (Integral Gradient) 本质上是一种归因分析 (Attribution Analysis) 方法。这一小节里面我们对归因分析方法做个总结，并推导积分梯度方法。 >>加入极市CV技术交流群，走在计算机视觉的最前沿

本文目录

积分梯度：一种归因分析方法
0 归因分析方法总结
1 预测概率对输入的梯度
2 预测概率对输入的梯度与输入的点乘
3 预测概率对输入的积分梯度 (Integrated Gradients)

0 归因分析方法总结

积分梯度 (Integral Gradient) 本质上是一种归因分析 (Attribution Analysis) 方法。这一小节里面我们对归因分析方法做个总结，并推导积分梯度方法。

基于分类问题归因分析中，一种重要的方法是Integrated Gradient(积分梯度)。这一小节我们做个汇总。

[1] How to Explain Individual Classification Decisions (The Journal of Machine Learning Research)
[2] Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps (ICLR 2014)
[3] Axiomatic attribution for deep networks (ICML 2017)
[4] Gradients of Counterfactuals

给定输入图片 和模型 ，模型是分类模型。归因分析 (Attribution Analysis) 方法会给出一张**归因图 (Attribution Map)**，这张图 对应模型 ，它与输入图片 的尺寸是一致的，代表了每个像素对最终输出的 "贡献度大小"。对于分类网络，这通常是每个特定的类别的贡献度。所谓归因，简单来说就是对于给定的输入图片 和模型 ，我们想办法指出 的哪些分量对模型的决策有重要影响，或者说对 的各个分量的重要性做个排序，用专业的话术来说那就是 "归因"。一个朴素的思路是直接使用 "预测概率对输入 的梯度 (Gradient w.r.t. )" 来作为 的各个分量的重要性指标，而积分梯度是对它的改进。

下面简单介绍下分类模型中几种计算归因图 (Attribution Map) 的方法。

1 预测概率对输入的梯度

该方法采用预测概率对输入 的梯度：

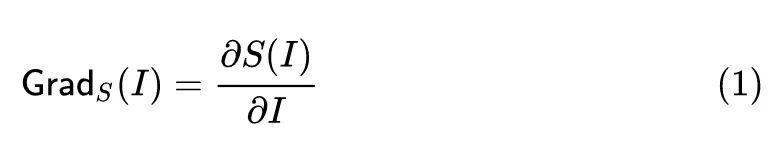
衡量了模型对输入的第 个分量变化的敏感程度，但是这种普通的计算预测概率对输入 的梯度的方法存在饱和问题 (典型的就是 ReLU 函数的负半轴)，即：梯度就为0了，那就揭示不出什么有效信息了。输入 发生一点点的变化将不会改变输出的概率。对于超分模型，饱和问题依旧存在。

2 预测概率对输入的梯度与输入的点乘

这种方法是为了解决上面的饱和问题：

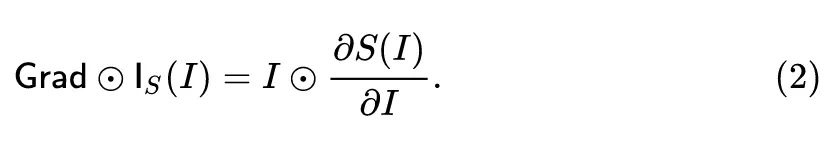
衡量了模型对输入的第 个分量变化的敏感程度。

3 预测概率对输入的积分梯度 (Integrated Gradients)

很多介绍积分梯度方法的文章 (包括原论文)，都过于生硬，没有很好地突出积分梯度方法是怎么推导过来的。本文试图用我自己的思路推导一下积分梯度方法的来龙去脉。

原论文认为归因分析 (Attribution Analysis) 方法应该首先满足两条基本的公理：

公理1：敏感性 (Sensitivity)

敏感性 (Sensitivity) 是指：任意的输入图片和基线图片，当其差值的某一部分发生了变化，导致模型的预测结果也发生变化时，归因图结果也应该能够表达出这种变化。

第1小节的方法1很显然是违背这个公理的。一个很直观的例子是 。假设 baseline 是 ，输入是 。当输入从 ，输出从0变化到1。但是因为输出自打 变化到1时就已经平了，没梯度了，所以归因图结果不发生变化。所以方法1显然丧失了敏感性。实际上，灵敏度的缺乏导致梯度集中在不相关的特征上。

公理2：实现不变性 (Implementation Invariance)

如果两个网络，尽管它们的实现方式非常不同，但是其输出对所有输入都相等，则这两个网络在功能上是等效的。举个例子：

• 网络1：
• 网络2：

其中， 

，

网络 和 就是功能相同的，即其输出对所有输入都相等，但是实现方式却不一致。

归因分析方法需要满足实现不变性 (Implementation Invariance)，即：对于两个功能相同的网络，尽管结构可能不一样，但是归因图的结果应该是相同的。

下面我们给大家从头推导积分梯度 (Integrated Gradients) 的方法。

在高等数学定积分章节里面，有下面的求解一元函数定积分的方法 (这个公式来自同济大学高等数学教材第七版)：

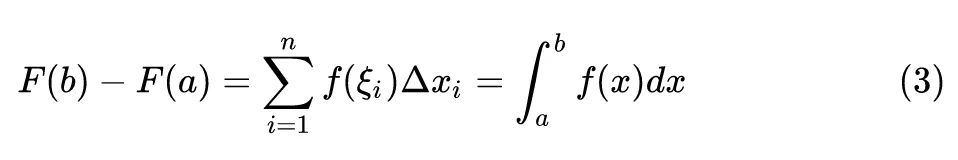
其中，第2项到第3项是通过令 得到的。这里的 都是标量。

如果把 换成矢量，则有下面的求解多元函数定积分的方法：

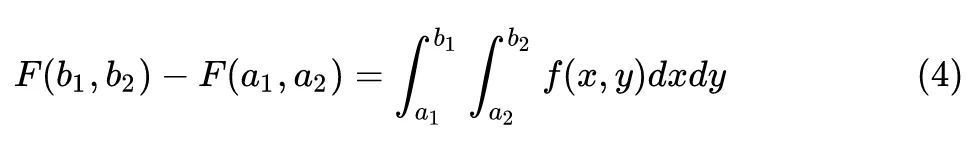
式中，函数 是个多元函数，其输入就可以看做是矢量了。这样一来和神经网络的联系就明朗了。

现在，我们把上式这个高等数学的表达换成神经网络的表达，就变成了：

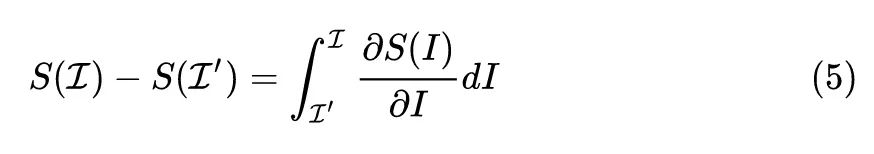
式中， 是介于 和 的一个中间变量。 相当于4式的多元函数 ， 和 则相当于是矢量输入。5式其实是个多重积分，因为自变量 是多元矢量： 。

把这个多重积分写成易于理解的展开式形式就是：

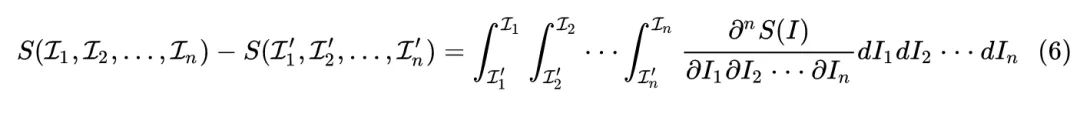
注意到 ，或者写成 就是当输入图片从 变化到 ，神经网络输出结果的变化量，是个标量。那么这个东西是没办法作为归因结果的，因为归因图必须是 维大小的。

接下来我们把6式变化一下：

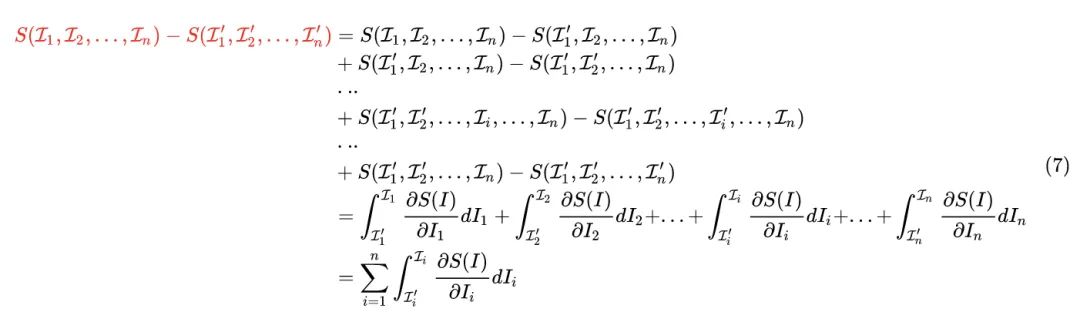
根据7式，我们看到：神经网络输出结果的变化量 其实是 个分量累加得到的，而这每个分量

恰好是第 个分量对输出变化的贡献。

所以积分梯度把

作为衡量了模型对输入的第 个分量的敏感程度。

我们假设 代表连接 和 的一条曲线，其中： 。那么 就可以表示为 。我们就把它代入7式，有：

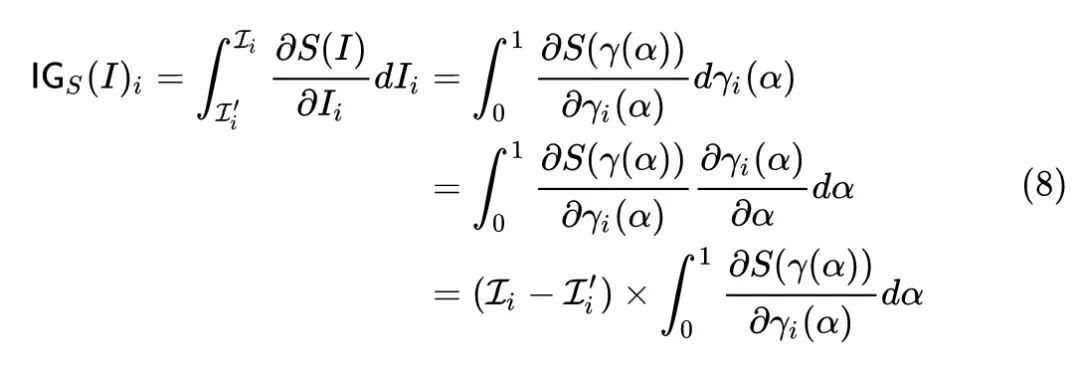
其中， 代表路径函数，最简单地可以取 ，代表连接 和 的一条直线。

衡量了模型对输入的第 个分量的敏感程度。下面我们把8式的下角标 去掉，依然将输入记为 ，Baseline 记为 ，积分梯度法的归因图 (Attribution Map) 的定义如下：

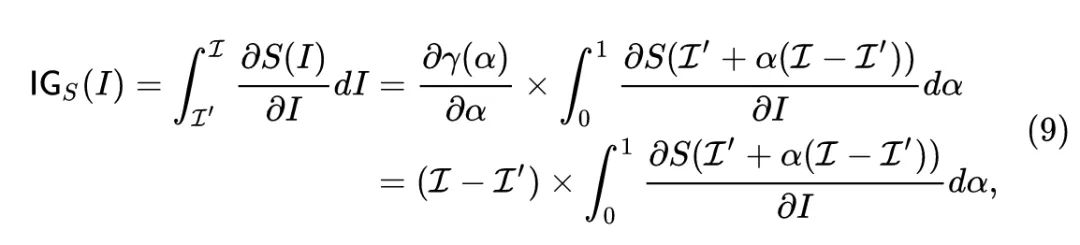
式中， 是插值参数。

根据7式，积分梯度满足：

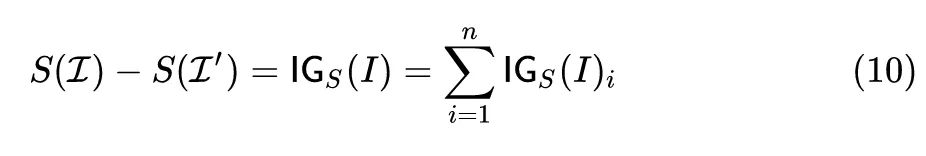
总结

积分梯度是一种神经网络归因分析的工具，能够很好地解决直接使用梯度进行归因分析时的 Gradient Saturation 问题。本文是我个人的一个思路推导。

公众号后台回复“数据集”获取火焰和烟雾图像数据集下载～

△点击卡片关注极市平台，获取 最新CV干货

极市干货

数据集资源汇总： 10个开源工业检测数据集汇总 ｜ 21个深度学习开源数据集分类汇总

算法trick ： 目标检测比赛中的tricks集锦 ｜ 从39个kaggle竞赛中总结出来的图像分割的Tips和Tricks

技术综述： 一文弄懂各种loss function ｜ 工业图像异常检测最新研究总结（2019-2020）

# 极市平台签约作者#

科技猛兽

知乎：科技猛兽

清华大学自动化系19级硕士

研究领域：AI边缘计算 (Efficient AI with Tiny Resource)：专注模型压缩，搜索，量化，加速，加法网络，以及它们与其他任务的结合，更好地服务于端侧设备。

作品精选

搞懂 Vision Transformer 原理和代码，看这篇技术综述就够了

用Pytorch轻松实现28个视觉Transformer，开源库 timm 了解一下！（附代码解读）

轻量高效！清华智能计算实验室开源基于PyTorch的视频 (图片) 去模糊框架SimDeblur

投稿方式：

添加小编微信Fengcall（微信号：fengcall19），备注：姓名-投稿

△长按添加极市平台小编

觉得有用麻烦给个在看啦~