【ICML2021】元学习的分布依赖分析

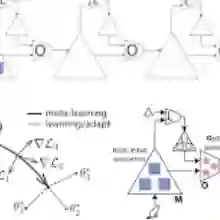
元学习理论的一个关键问题是如何理解任务分布对迁移风险的影响，即从未知任务分布中得出的元学习器对新任务的预期错误。本文针对高斯噪声和高斯任务(或参数)分布的固定设计线性回归问题，给出了任意算法的分布相关的迁移风险下界，同时给出了一种新的，所谓的偏置正则化回归方法的加权版本能够将这些下界匹配到一个固定的常数因子。值得注意的是，权重是由高斯任务分布的协方差得到的。总之，我们的结果提供了在这种高斯设置下元学习的困难的精确表征。虽然这个问题设置可能看起来很简单，但我们证明它足够丰富，可以统一元学习的“参数共享”和“表示学习”流; 特别地，表示学习是作为任务分布的协方差矩阵未知的特殊情况得到的。在这种情况下，我们提出采用EM方法，这在我们的情况下显示了有效的更新。本文通过对EM的实证研究完成，实验结果表明，EM算法可以随着任务数量的增加而达到下界，同时在表示学习环境中，该算法也能成功地与其他算法相媲美。

https://icml.cc/Conferences/2021/Schedule?showEvent=10047