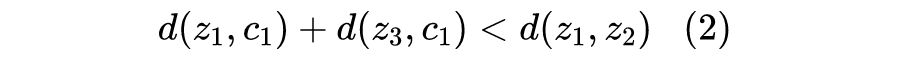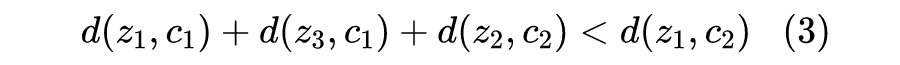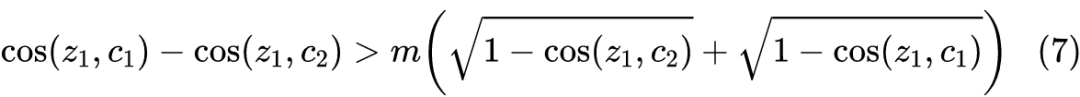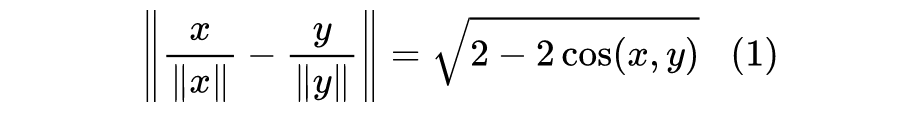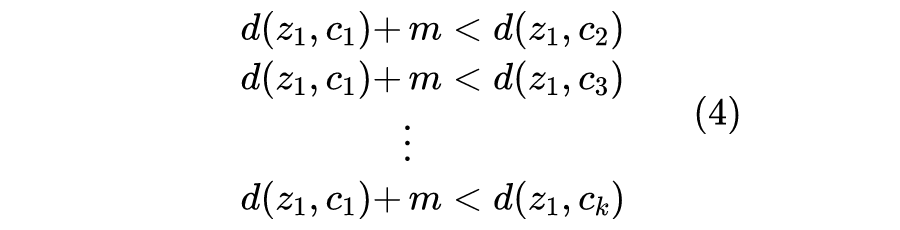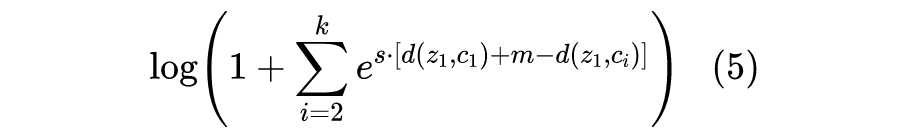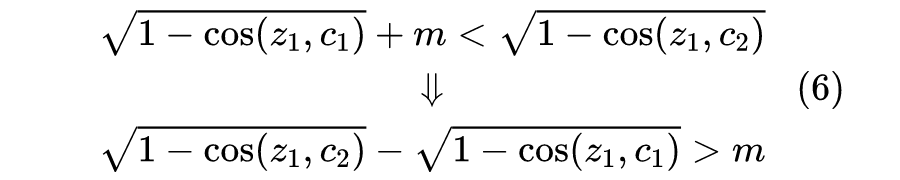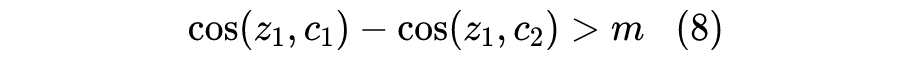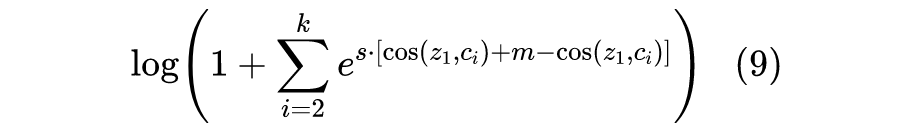从三角不等式到Margin Softmax

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 追一科技

研究方向 | NLP、神经网络

在《基于 GRU 和 am-softmax 的句子相似度模型》中我们介绍了 AM-Softmax，它是一种带 margin 的 softmax，通常用于用分类做检索的场景。当时通过图示的方式简单说了一下引入 margin 是因为“分类与排序的不等价性”，但没有比较定量地解释这种不等价性的来源。

在这篇文章里，我们来重提这个话题，从距离的三角不等式的角度来推导和理解 margin 的必要性。

三角不等式

平时，我们说的距离一般指比较直观的“欧氏距离”，但在数学上距离，距离又叫“度量”，它有公理化的定义，是指定义在某个集合上的二元函数 ，满足：

1. 非负性： ；

2. 同一性： ；

3. 对称性： ；

4. 三角不等式： 。

顾名思义，距离是用来度量 之间的差异程度的。理论上来说，只要满足前两点要求，就可以用来度量差异了，比如概率里边常用的 KL 散度，就仅仅满足前两点。第 3、4 点的加入，本质上来说是为了使得这样定义出来的距离与我们常见的欧氏距离更加接近，比如对称性是“距离没有方向”的体现，而三角不等式是“两点之间直线最短”的体现，这些类似有利于我们通过欧氏距离的类比来思考更一般的距离。

从这个定义来看，深度学习其实比较少碰到符合上述 4 点要求的距离，比如通常的分类是直接用内积加 softmax，而内积只满足第三点；余弦距离 也只满足前 3 点，不满足第 4 点。不过，某些函数我们可以微调一下定义，使得它成为一个距离，比如我们知道欧氏距离是满足三角不等式的，所以

必然也满足三角不等式。所以，余弦距离 是不满足三角不等式的，但是改为 就满足了。

分类与排序

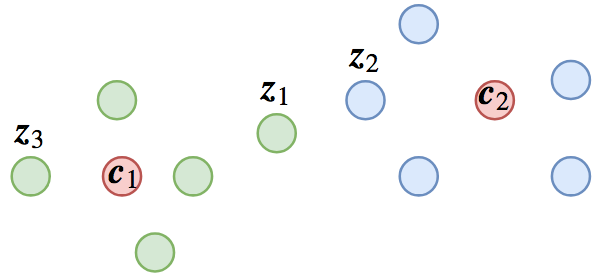
像人脸识别或者句子相似度等场景，在预测阶段我们是拿特征去排序的，我们自然希望随便拿一个样本，就能够检索出所有同类样本，这就要求“类内差距小于类间差距”；但是，如果我们将其作为分类任务训练的话，则未必能达到这个目的，因为分类任务的目标是“最靠近所属类的中心”。具体例子可以参考下图：

▲ 一种可能的分类结果，其中红色点代表类别中心，其他点代表样本

在该图中， 属于类 输于类 ，从分类角度来看 ，因此分类都是正确的，但是 ，所以用 去检索的话，找到的是不同类的 ，而不是同类的 。

我们可以通过三角不等式更加定量地描述这种不等关系：我们希望达到 ，根据三角不等式有 ，所以一个充分的条件是

两端加上 ，并利用三角不等式 ，我们得到上式的一个充分条件是

要注意的是，分类任务只要求对于 来说有 ，而上式多出了 ，多出来的一项就是 margin 项。

注意到 分别是样本 到其所属类中心的距离，所以我们可以认为 是“类平均直径”，它应该接近一个常数 ，我们可以将它作为超参数调整。如果要自适应调整的话，可以考虑先 训练一段时间，然后估计“类平均直径”作为 再训练，然后再重新估计 并训练，等等。

AM-Softmax

通过上面的推导，我们知道为了保证分类模型的特征可以用于排序，那么每个样本不仅仅要最靠近类中心，而且是距离加上 之后还要最靠近类中心，即如果 属于类 的话，那么就要求：

根据《将“softmax+交叉熵”推广到多标签分类问题》里边的思路：只要我们希望 ，就可以往 里边加入 来构造 loss。所以我们就可以构造如下的 loss：

这便是带加性 margin 的交叉熵，其中 是缩放比例，相当于 softmax 的温度参数。

不过别忘了，上述推导都是基于 满足三角不等式，而我们平常用的打分函数并不满足三角不等式。对于训练检索模型来说，我们通常用余弦距离来打分，前面说了余弦距离可以通过开根号来满足三角不等式，所以对应的要求变为（以 为例）：

两边乘以 得到

显然右端是有上界的，所以适当调整 ，可以使得

成为一个充分条件，这时候对应的 margin 交叉熵是

这就是 AM-Softmax。

回顾与小结

本文从三角不等式的角度推导了用分类模型做排序任务时 margin 的必要性，假定所用的打分函数满足三角不等式的前提下，能比较自然地导出相关结果。

特别鸣谢

感谢 TCCI 天桥脑科学研究院对于 PaperWeekly 的支持。TCCI 关注大脑探知、大脑功能和大脑健康。

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·