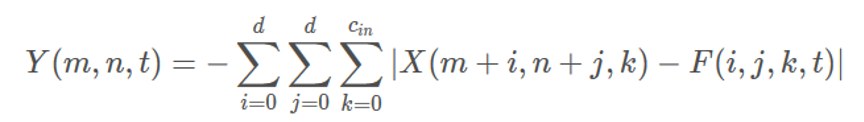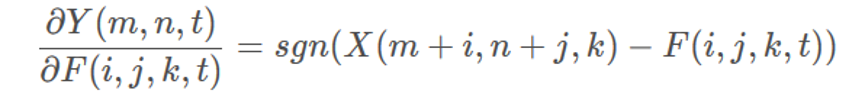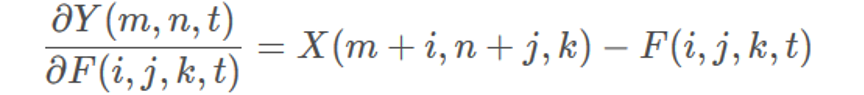给卷积神经网络动动刀：加法网络探究

2020 年 7 月 26 日 AI科技评论

卷积神经网络（CNN）在计算机视觉任务中有着广泛的应用，然而它的运算量非常巨大，这使得我们很难将CNN直接运用到计算资源受限的移动设备上。为了减少CNN的计算代价，许多模型压缩和加速的方法被提出。

其中AdderNet就是一种从新角度对模型进行加速的方法，以往的模型加速方法通过减少CNN的参数，AdderNet通过重新定义卷积计算，将卷积中的乘法替换为了加法。我们知道，乘法的计算代价要远远大于加法，AdderNet通过这种方式减少了计算量。

图1 加法和乘法计算量对比

CNN卷积计算：

AdderNet计算：

代码解读

AdderNet的训练代码已经在github上开源（https://github.com/huawei-noah/AdderNet），接下来我们对代码进行分析和解读。

AdderNet的训练代码主要分为几个文件：

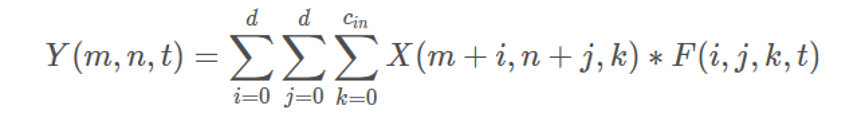
adder.py
main.py
resnet20.py
resnet50.py
test.py

其中adder.py定义了AdderNet的基础算子，main.py是训练AdderNet的文件，test.py是测试文件，resnet20.py和resnet50.py定义了网络结构。

由于训练和测试的代码以及网络结构的代码和正常的卷积神经网络一样，这里我们不对它们做解析，我们主要解读定义adder算子的adder.py文件。

adder.py中共含有两个类和一个函数，两个类分别是adder2d和adder，一个函数为adder2d_function。我们首先来看adder2d这个类。

class adder2d(nn.Module): def __init__(self, input_channels, output_channels, kernel_size, stride=1, padding=0, bias=False): super(adder2d, self).__init__() self.stride = stride self.padding = padding self.input_channel=output_channel self.kernel_size=kernel_size self.adder=torch.nn.Parameter(nn.init.normal_(torch.randn(output_channel,input_channel,kernel_size,kernel_size))) self.bias=bias if bias: self.b = torch.nn.Parameter(nn.init.uniform_(torch.zeros(output_channel))) def forward(self, x): output = adder2d_function(x,self.adder, self.stride, self.padding) if self.bias: output += self.b.unsqueeze(0).unsqueeze(2).unsqueeze(3) return output

可以看到，adder2d这个类定义了adder算子，是继承于nn.module的，所以在网络定义时可以直接使用adder2d来定义一个adder层。例如resnet20.py中就如下定义一个3*3 kernel大小的adder层：

def conv3x3(in_planes, out_planes, stride=1): " 3x3 convolution with padding " return adder.adder2d(in_planes, out_planes, kernel_size=3, stride=stride, padding=1, bias=False)

可以看到adder2d的使用方式和nn.Conv2d基本完全一样。

接下来我们进一步解读adder2d包含的属性，和卷积算子相同，adder算子包括几个属性：stride，padding，input_channel，output_channel和kernel_size，给定这几个属性后，adder2d就会根据这些属性定义adder filter和bias

self.adder= torch.nn.Parameter(nn.init.normal_(torch.randn(output_channel,input_channel,kernel_size,kernel_size))) self.b = torch.nn.Parameter(nn.init.uniform_(torch.zeros(output_channel)))

最后对前向传播使用函数adder2d_function来得到结果

output= adder2d_function(x,self.adder, self.stride, self.padding)

所以接下来我们进一步分析adder2d_function这个函数是如何进行adder算子的运算的：

def adder2d_function(X, W, stride=1, padding=0): n_filters, d_filter, h_filter, w_filter = W.size() n_x, d_x, h_x, w_x = X.size() h_out = (h_x - h_filter + 2 * padding) / stride + 1 w_out = (w_x - w_filter + 2 * padding) / stride + 1 h_out, w_out = int(h_out), int(w_out) X_col = torch.nn.functional.unfold(X.view(1, -1, h_x, w_x), h_filter, dilation=1, padding=padding, stride=stride).view(n_x, -1, h_out*w_out) X_col = X_col.permute(1,2,0).contiguous().view(X_col.size(1),-1) W_col = W.view(n_filters, -1) out = adder.apply(W_col,X_col) out = out.view(n_filters, h_out, w_out, n_x) out = out.permute(3, 0, 1, 2).contiguous() return out:

可以看到，adder2d_function将输入X和卷积核W先进行了一系列变换，变换为W_col和X_col两个矩阵后再进行计算，这和卷积的计算十分类似，在卷积中，我们通常将输入图片通过im2col变换变为矩阵，将卷积核reshape成矩阵，将卷积计算转换为矩阵乘法运算进行。这里adder的计算也是同样的：

X_col = torch.nn.functional.unfold(X.view(1, -1, h_x, w_x), h_filter, dilation=1, padding=padding, stride=stride).view(n_x, -1, h_out*w_out) X_col = X_col.permute(1,2,0).contiguous().view(X_col.size(1),-1)

上面两行代码就是将输入的X进行im2col变成二维矩阵

W_col = W.view(n_filters, -1)

同样的W也reshape成二维矩阵。

接下来如果我们要进行卷积，就将这两个矩阵进行矩阵乘法的运算。然而我们现在进行的是adder运算，相当于将卷积中的乘法改为加法，所以需要重新定义这个矩阵运算：

out = adder.apply(W_col,X_col)

可以看到adder.apply就是重新定义的对应加法神经网络的矩阵运算。

out = out.view(n_filters, h_out, w_out, n_x) out = out.permute(3, 0, 1, 2).contiguous()

最后得到的output矩阵同样通过reshape变回4维。

接下来我们仔细分析这个adder运算是如何实现的。

class adder(Function): @staticmethod def forward(ctx, W_col, X_col): ctx.save_for_backward(W_col,X_col) output = -(W_col.unsqueeze(2)-X_col.unsqueeze(0)).abs().sum(1) return output @staticmethod def backward(ctx,grad_output): W_col,X_col = ctx.saved_tensors grad_W_col = ((X_col.unsqueeze(0)-W_col.unsqueeze(2))*grad_output.unsqueeze(1)).sum(2) grad_W_col = grad_W_col/grad_W_col.norm(p=2).clamp(min=1e-12)*math.sqrt(W_col.size(1)*W_col.size(0))/5 grad_X_col = (-(X_col.unsqueeze(0)-W_col.unsqueeze(2)).clamp(-1,1)*grad_output.unsqueeze(1)).sum(0) return grad_W_col, grad_X_col

这个adder运算分为两部分：前向传播和反向传播。

我们先来看前向传播的部分，只用了很简单的一句代码来实现：

output = -(W_col.unsqueeze(2)-X_col.unsqueeze(0)).abs().sum(1)

实际上这个代码就是将矩阵乘法中的乘法运算用减法和绝对值来代替，我们回顾矩阵乘法，其实就是将两个矩阵的中间维度进行对应点的相乘后再相加，假设是m*n的矩阵A和n*k的矩阵B相乘，可以将A在第三个维度复制k份，将B在第零个维度复制m份，得到m*n*k大小的矩阵A和B，将这两个矩阵每个点相乘，最后再第二个维度求和，就得到了m*k的矩阵，也就是矩阵乘法的输出结果，这其实就是上面代码的实现过程，将W在第三个维度扩充，将X在第一个维度扩充，然后相减取绝对值，在第二个维度求和，就得到了adder的矩阵运算结果。

我们知道，在pytorch如果你定义好前向传播，pytorch是会对它进行自动求导的，然而在AdderNet里，反向传播的梯度和真实梯度不一样，所以我们要自己定义这个反向传播的梯度。

AdderNet中真实梯度为：

梯度被修改为：

和

所以，和上面前向传播类似的矩阵计算方法，可以用以下代码计算反向传播的值，再乘上链式法则中输出的梯度，就得到了W和X的梯度。

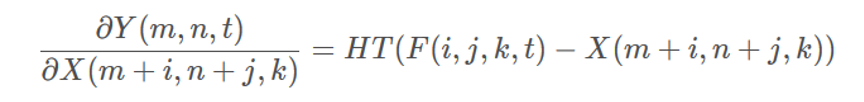
grad_W_col= ((X_col.unsqueeze(0)-W_col.unsqueeze(2))*grad_output.unsqueeze(1)).sum(2) grad_X_col = (-(X_col.unsqueeze(0)-W_col.unsqueeze(2)).clamp(-1,1)*grad_output.unsqueeze(1)).sum(0)

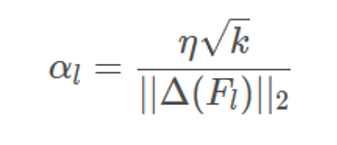
最后再加上论文中提到的adaptive learning rate：

代码可以表示为：

grad_W_col=grad_W_col/grad_W_col.norm(p=2).clamp(min=1e-12)*math.sqrt(W_col.size(1)*W_col.size(0))/5

以上就是对AdderNet开源代码的完整解读。

结果

我们最后来看看AdderNet的实验结果。

可以发现，AdderNet在CIFAR-10和ImageNet数据集上都取得了和CNN相似准确率的结果，并且基本不需要任何乘法，使用github开源的代码就可以复现以上的结果。

当然，目前AdderNet的训练还是十分慢的，作者说这是因为AdderNet没有cuda实现加速，主要的运行速度在于adder这个矩阵计算函数。我们在这里提供一个简单的思路来实现cuda加速，我们先参考矩阵乘法的cuda实现https://github.com/NVIDIA/cuda-samples/blob/master/Samples/matrixMul/matrixMul.cu，将矩阵乘法中的乘改为减法和绝对值就可以了，最后，我们可以通过pytorch自带的cuda extension来编译cuda代码（https://pytorch.org/tutorials/advanced/cpp_extension.html），就可以完成AdderNet的cuda加速了。

该论文已被CVPR 2020接收。

论文一作：

陈汉亭，北京大学智能科学系硕博连读三年级在读，同济大学学士，师从北京大学许超教授，在华为诺亚方舟实验室实习。研究兴趣主要包括计算机视觉、机器学习和深度学习。在 ICCV,AAAI,CVPR 等会议发表论文数篇，目前主要研究方向为神经网络模型小型化。

论文二作：

王云鹤，在华为诺亚方舟实验室从事边缘计算领域的算法开发和工程落地，研究领域包含深度神经网络的模型裁剪、量化、蒸馏和自动搜索等。王云鹤博士毕业于北京大学，在相关领域发表学术论文40余篇，包含NeurIPS、ICML、CVPR、ICCV、TPAMI、AAAI、IJCAI等。