卷积神经网络四种卷积类型

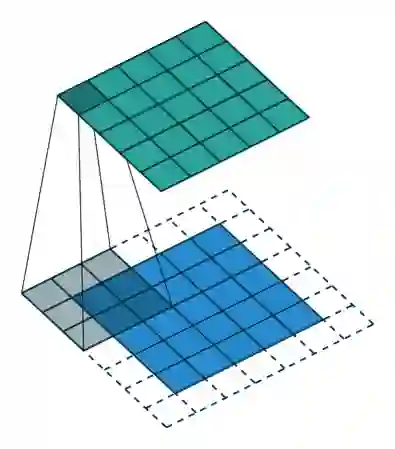
使用内核大小为3，步长为1和填充的2D卷积

一般卷积

首先，我们需要就定义卷积层的一些参数达成一致。

卷积核大小（Kernel Size）：卷积核定义了卷积的大小范围，二维卷积核最常见的就是 3*3 的卷积核。

步长（Stride）：步长定义了当卷积核在图像上面进行卷积操作的时候，每次卷积跨越的长度。在默认情况下，步长通常为 1，但我们也可以采用步长是 2 的下采样过程，类似于 MaxPooling 操作。

填充（Padding）：卷积层采用一定数量的输入通道（I），并且设计特定数量的输出通道（O）。每一层所需的参数可以通过 I*O*K 来进行计算，其中 K 等于卷积核的数量。

输入和输出管道（Input & Output Channels）：卷积层采用一定数量的输入通道

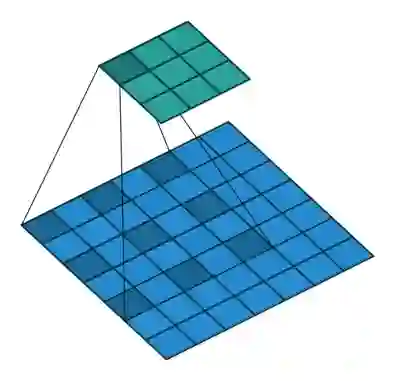
扩张的卷积

使用3内核进行2D卷积，扩展率为2且无填充

扩张的卷积为卷积层引入另一个参数，称为扩张率。这定义了卷积核中值之间的间距。扩张率为2的3x3内核与5x5内核具有相同的视野，而仅使用9个参数。想象一下，获取一个5x5内核并删除每一个第二列和第二行（间隔删除），就是我们介绍的卷积。

这以相同的计算成本提供了更宽的视野。扩张卷积在实时分割领域中特别受欢迎。如果您需要广泛的视野并且无法承受多个卷积或更大的核，请使用它们。

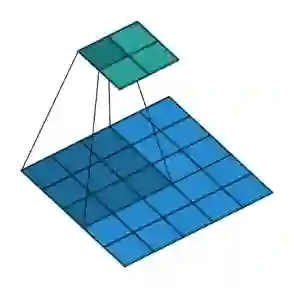
转置卷积

（又称解卷积或分数跨度卷积）

有些消息来源使用名称deconvolution，这是不合适的，因为它不是解卷积。为了使事情更糟，确实存在解卷积，但它们在深度学习领域并不常见。实际的反卷积会使卷积过程恢复。想象一下，将图像输入到单个卷积层中。现在取出输出，将它扔进一个黑盒子里然后再出现原始图像。这个黑盒子进行反卷积。它是卷积层的数学逆。

转置卷积有点类似，因为它产生与假设的反卷积层相同的空间分辨率。但是，对值执行的实际数学运算是不同的。转置卷积层执行常规卷积，但恢复其空间变换。

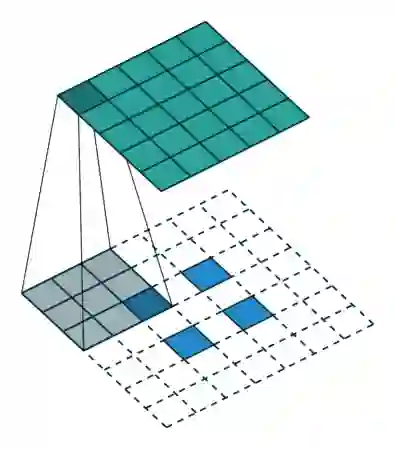
2D卷积，没有填充，步幅为2，内核为3

此时你应该很困惑，让我们看一个具体的例子。将5×5的图像送入卷积层。步幅设置为2，填充停用，内核为3x3。这导致2x2图像。

如果我们想要反转这个过程，我们需要逆数学运算，以便从我们输入的每个像素生成9个值。然后，我们以2的步幅遍历输出图像。这将是反卷积。

转换2D卷积，没有填充，步幅为2，内核为3

转置卷积不会这样做。的共同点是它保证输出也是5x5图像，同时仍然执行正常的卷积操作。为此，我们需要在输入上执行一些花哨的填充。

正如您现在可以想象的那样，此步骤不会从上面颠倒过程。至少不涉及数值。

它只是从之前重建空间分辨率并执行卷积。这可能不是数学逆，但对于编码器 - 解码器架构，它仍然非常有用。这样我们就可以将图像的升级与卷积相结合，而不是进行两个单独的处理。

可分离的卷积

在可分离的卷积中，我们可以将内核操作分成多个步骤。让我们将卷积表示为y = conv（x，k），其中y是输出图像，x是输入图像，k是核。简单。接下来，假设k可以通过以下公式计算：k = k1.dot（k2）。这将使它成为可分离的卷积，因为我们可以通过用k1和k2进行2个1D卷积来得到相同的结果，而不是用k进行2D卷积。

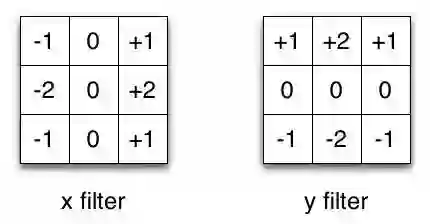
Sobel X和Y滤镜

以Sobel内核为例，它通常用于图像处理。你可以通过乘以向量[1,0，-1]和[1,2,1] .T得到相同的内核。在执行相同操作时，这将需要6个而不是9个参数。上面的例子显示了所谓的空间可分卷积，据我所知，它不用于深度学习。

编辑：实际上，通过堆叠1xN和Nx1内核层，可以创建与空间可分离卷积非常相似的东西。这最近在一个名为EffNet的架构中使用，显示了有希望的结果。

在神经网络中，我们通常使用称为深度可分离卷积的东西。这将执行空间卷积，同时保持通道分离，然后进行深度卷积。在我看来，通过一个例子可以较好地理解它。

假设我们在16个输入通道和32个输出通道上有一个3x3卷积层。详细情况是，32个3x3核遍历16个通道中的每个通道，产生512（16x32）个特征映射。接下来，我们通过添加它们来合并每个输入通道中的1个特征图。由于我们可以做32次，我们得到了我们想要的32个输出通道。

对于同一示例中的深度可分离卷积，我们遍历16个通道，每个通道有1个3x3内核，为我们提供了16个特征映射。现在，在合并任何东西之前，我们遍历这16个特征映射，每个特征映射有32个1x1卷积，然后才开始将它们加在一起。这导致656（16x3x3 + 16x32x1x1）参数与上面的4608（16x32x3x3）参数相反。

该示例是深度可分离卷积的特定实现，其中所谓的深度乘数为1.这是迄今为止这种层的最常见设置。我们这样做是因为空间和深度信息可以解耦的假设。看一下Xception模型的表现，这个理论似乎有效。由于其有效使用参数，深度可分离卷积也用于移动设备。

声明：本文版权归原作者所有，文章收集于网络，为传播信息而发，如有侵权，请联系小编及时处理，谢谢！

文章来源：今日头条

《机器读心术之神经网络与深度学习》通过学习熟悉神经网络技术和深度学习，懂得怎样运用到自己的实际工作，设计有一定规模的学习系统，智能化地解决某些场景的实际问题。个人技术能力和数据分析能力，知识见解有明显增长。点击下方二维码报名课程