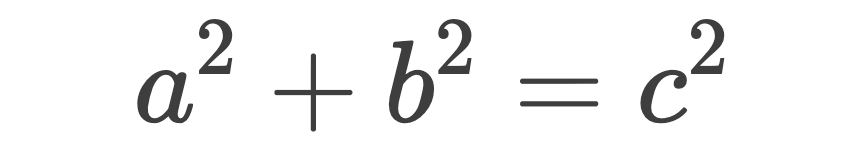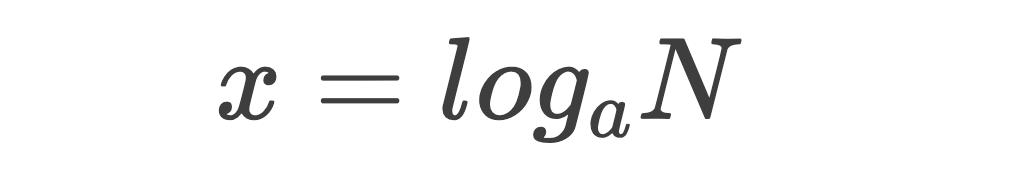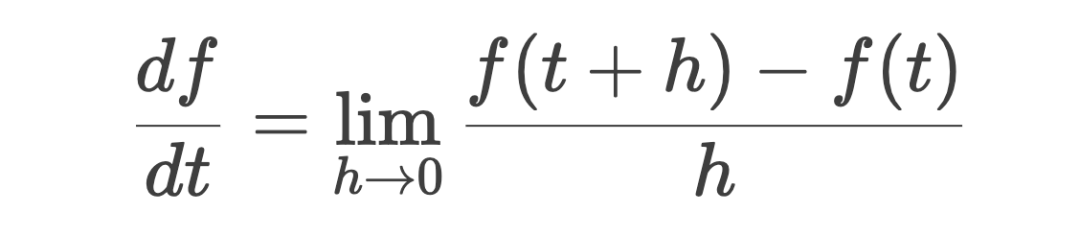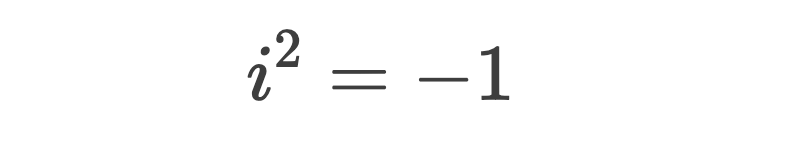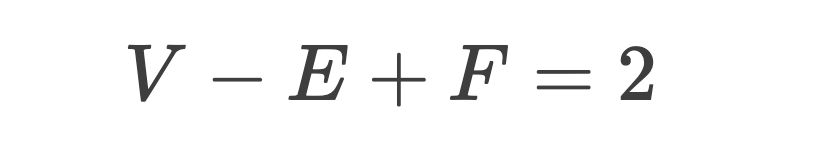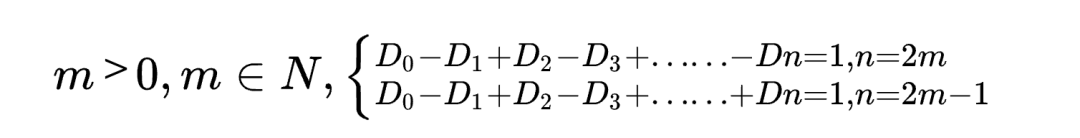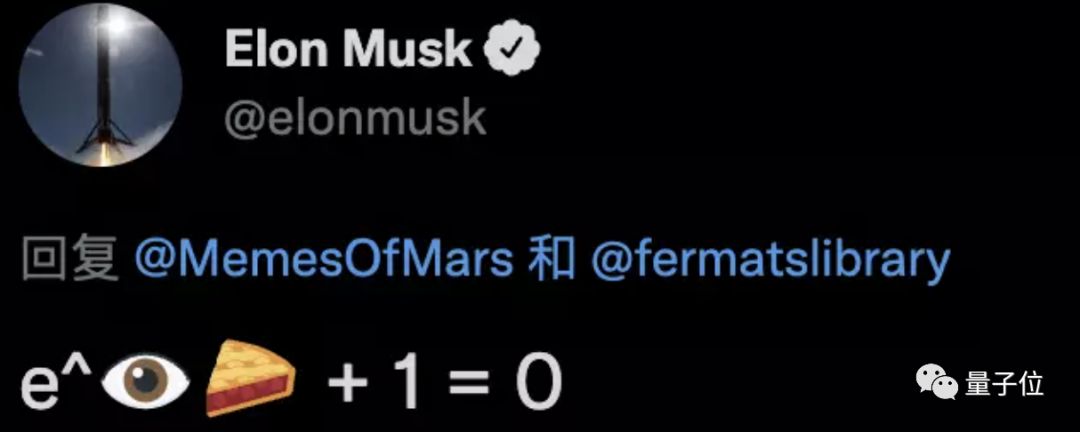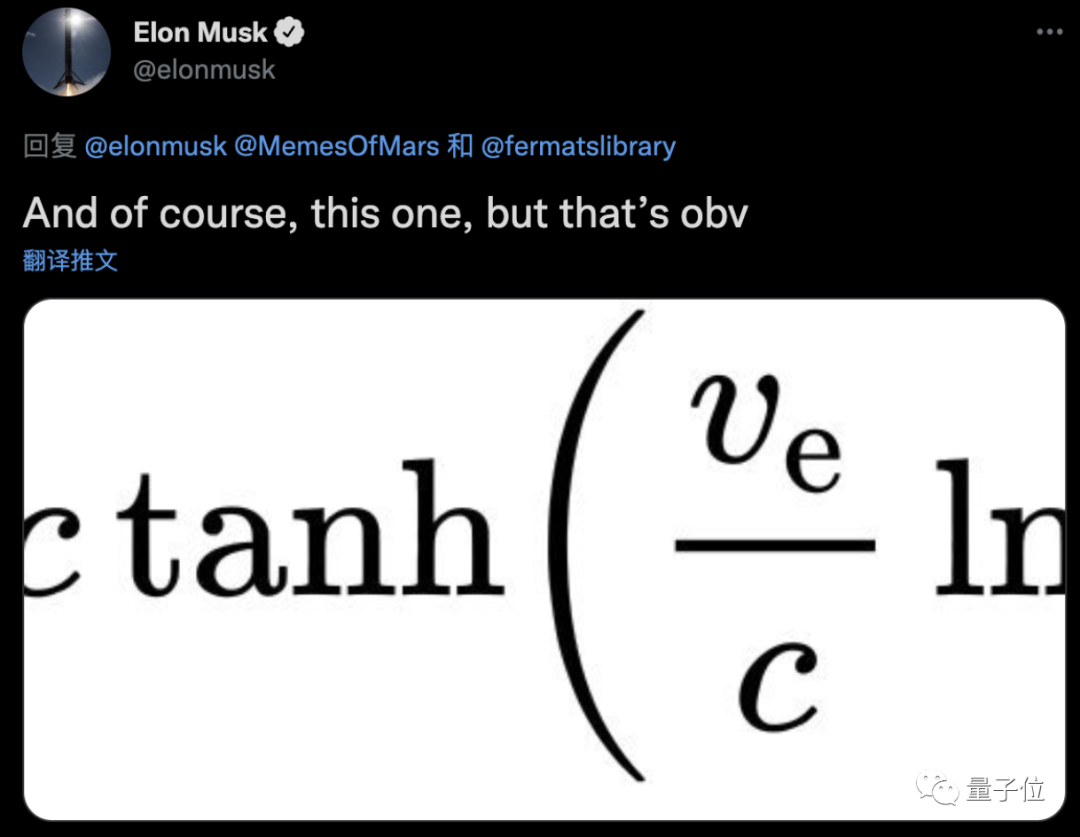17个改变世界的数学公式，马斯克点赞

金磊 发自 凹非寺
量子位 | 公众号 QbitAI

到底是什么样的公式，能让“钢铁侠”马斯克下场点赞？

答：

它们改变了世界。

被给予如此高度评价的公式，一共包含17个：

而且这位博主发布推文才短短数小时，便揽获了19000个“点赞”，火爆程度可见一斑。

那么这些公式，到底是如何改变了世界？

以及马斯克又pick了哪个呢？（文末揭晓答案）

1、勾股定理

英文：

Pythagoras’ Theorem

公式：

定义：

在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。

这个基本几何定理，在公元前11世纪，数学家商高（西周初年人）就提出“勾三、股四、弦五”。

而在西方，希腊数学家毕达哥拉斯在公元前6世纪证明了勾股定理，因而西方人都习惯地称这个定理为毕达哥拉斯定理（Pythagoras’ Theorem）。

（“老毕”还证明过黄金分割线，他创办的毕达哥斯拉学派是古希腊四大门派之一。）

勾股定理被认为是论证几何的发端，它是历史上第一个把数与形联系起来的定理，也是历史上第一个给出了完全解答的不定方程。

这条定理不仅在几何学中是一颗光彩夺目的明珠，更是被誉为“几何学的基石”。

2、对数

英文：

Logarithms

公式：

定义：

如果a的x次方等于N（a>0，且a≠1），那么数x叫做以a为底N的对数。

对数方法是由数学家约翰·皮纳尔在1614年发明。

但这个方法无论是放在当时还是现在，都具有重要意义，它的出现让许多繁难的计算成为了可能。

也正因如此，在计算器和计算机出现之前，它持久地被用于测量、航海以及其他实用数学分支中。

3、微积分

英文：

Calculus

公式：

此处给出的公式，是微积分中导数的定义。

其实微积分是高等数学中研究函数的微分（Differentiation）、积分（Integration）以及有关概念和应用的数学分支。

微分学包括求导数的运算，是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。

而积分学，包括求积分的运算，为定义和计算面积、体积等提供一套通用的方法。

冯·诺依曼曾经这样评价微积分：

它是现代数学的第一个成就，而且怎样评价它的重要性都不为过。

我认为，微积分比其他任何事物都更清楚地表明了现代数学的发端；而且，作为其逻辑发展的数学分析体系仍然构成了精密思维中最伟大的技术进展。

许多初等数学无法解决的问题，微积分往往都可以迎刃而解，而且许多自然现象也可以通过建立微分方程来描述。

也正因如此，微积分广泛地被应用于运动学、天文学、经济学、社会学、化学、生物学等。

4、万有引力定律

英文：

Law of Gravity

公式：

定义：

任何两个质点都存在通过其连心线方向上的相互吸引的力：

该引力大小与它们质量的乘积成正比与它们距离的平方成反比，与两物体的化学组成和其间介质种类无关。

其中，F表示两个物体之间的引力；G表示万有引力常量；m₁和m₂分别表示物体1和物体2的质量；r则是两个物体之间的距离（大小）。

万有引力定律是牛顿于1687年在《自然哲学的数学原理》上所发表，可以说是17世纪自然科学最伟大的成果之一。

他用万有引力定律证明了开普勒定律、月球绕地球的运动、潮汐的成因和地球两极较扁等自然现象。

因此，牛顿的万有引力定律是天体力学的基础。人造卫星、月球和行星探测器的轨道，都是以这个定律为基础来计算的。

5、-1的平方根

英文：

The square root of -1

公式：

数学家们一直在对数字的概念做着拓展工作，例如从自然数到负数、分数，再到实数。

而在16世纪，意大利米兰学者卡当首次引入了复数的概念。

经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，这个概念逐渐被数学家接受。

从数学角度来看，复数可以说是极其优雅，任何方程都有一个复数解，但这种情况在实数却不成立。

例如，对于x² + 4 = 0，就是没有实数解的，而放眼复数，解就是-4或2i。

而微积分也是可以拓展到复数，数学家们由此还发现了一些数所具备的对称性和性质。

这些特性便使得复数在电子学和信号处理中起到了重要的作用。

6、多面体欧拉定理

英文：

Euler’s Polyhedra Formula

公式：

定义：

对于n维空间中的简单多面体，其零维对象数（即顶点数）D₀、一维对象数（即边数）D₁、二维对象数（即面数）D₂、三维对象数（即体数）D₃、……、n维对象数D_n：

其中符号为正负号交替出现，等式一边是各维对象数的重复加减，等式另一边是1。

一般以V（Vertex）表示零维对象（即顶点）数D₀，以E（Edge）表示一维对象（即边、棱）数D₁，以F（Flat surface）表示二维对象（即面）数D₂，以S（Solid）表示三维对象（即体）数D₃，以P表示四维对象数D₄。

对于一般的三维空间，该公式表达为：V - E + F - S= 1。

由于对于一个三维物体，其体数S总是1，因此就得到上述的那个公式。

欧拉的这项观察，现在被视为拓扑不变性的最早的例子之一。

连同他对柯尼斯堡桥问题的解决，可以说是为拓扑学的发展铺平了道路，使其成为现代物理学必不可少的一个数学分支。

……

由于篇幅原因，其它公式便不一一展开，感兴趣的友友们可以访问文末链接查看详情。

马斯克pick了哪个公式？

最后，揭晓开头的答案。

马斯克喜欢的公式是：

翻译过来就是——e^iπ + 1 = 0，即被称为史上最美公式的欧拉公式。

除此之外，马斯克还表示喜欢下面这个公式：

……

总而言之，许多网友在看完这份公式列表之后，纷纷发出了如下的感慨：

那么你最喜欢的公式是哪个呢？欢迎在评论区留言分享

参考链接：

[1]https://www.businessinsider.com/17-equations-that-changed-the-world-2014-3#1-the-pythagorean-theorem-1
[2]https://twitter.com/gunsnrosesgirl3/status/1500925968956993540

— 完 —

「人工智能」、「智能汽车」微信社群邀你加入！

欢迎关注人工智能、智能汽车的小伙伴们加入我们，与AI从业者交流、切磋，不错过最新行业发展&技术进展。

ps.加好友请务必备注您的姓名-公司-职位哦~

点这里👇关注我，记得标星哦～

一键三连「分享」、「点赞」和「在看」

科技前沿进展日日相见~