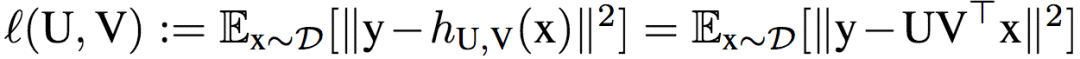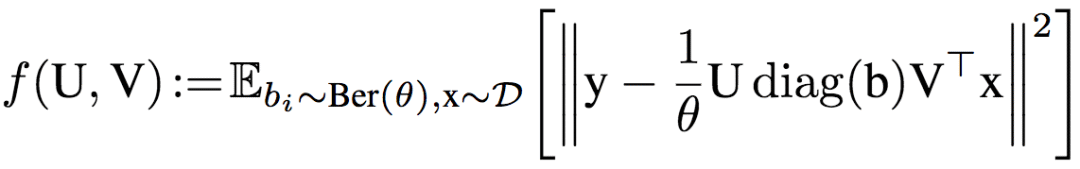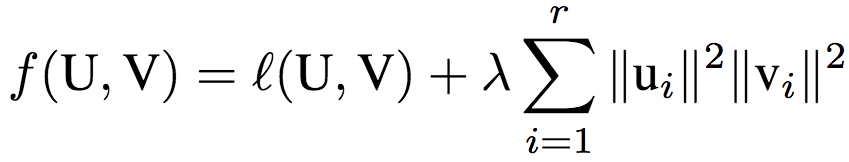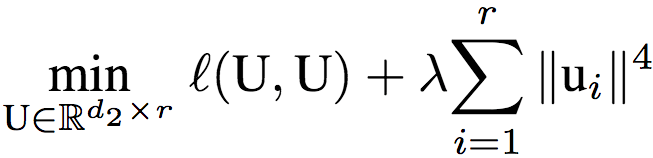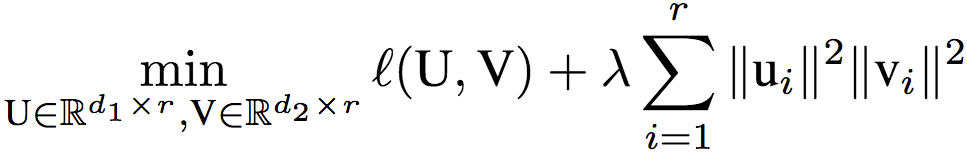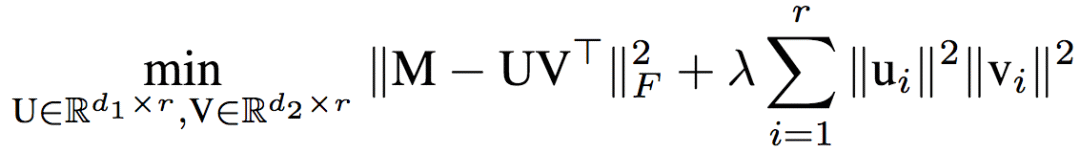dropout的隐式偏置

2018 年 6 月 29 日 论智

来源：arXiv

编译：weakish

现代的深度神经网络通常具有海量参数，甚至高于训练数据的大小。这就意味着，这些深度网络有着强烈的过拟合倾向。缓解这一倾向的技术有很多，包括L1、L2正则、及早停止、组归一化，以及dropout。在训练阶段，dropout随机丢弃隐藏神经元及其连接，以打破神经元间的共同适应。尽管dropout在深度神经网络的训练中取得了巨大的成功，关于dropout如何在深度学习中提供正则化机制，目前这方面的理论解释仍然很有限。

最近，约翰·霍普金斯大学的Poorya Mianjy、Raman Arora、Rene Vidal在ICML 2018提交的论文On the Implicit Bias of Dropout，重点研究了dropout引入的隐式偏置。

基于权重系联的线性自动编码器

为了便于理解dropout的作用机制，研究人员打算在简单模型中分析dropout的表现。具体而言，研究人员使用的简单模型是只包含一个隐藏层的线性网络。该网络的目标是找到最小化期望损失（平方损失）的权重矩阵U、V：

上式中，x为输入，y为标注输出，D为输入x的分布，h表示隐藏层。

学习算法为带dropout的随机梯度下降，其目标为：

其中，dropout率为1-θ，具体的算法为：

这一算法的目标等价于（推导过程见论文附录A.1）：

其中，λ = (1-θ)/θ

研究人员又令U = V，进一步简化模型为权重系联的单隐藏层线性自动编码器。相应地，该网络的目标为：

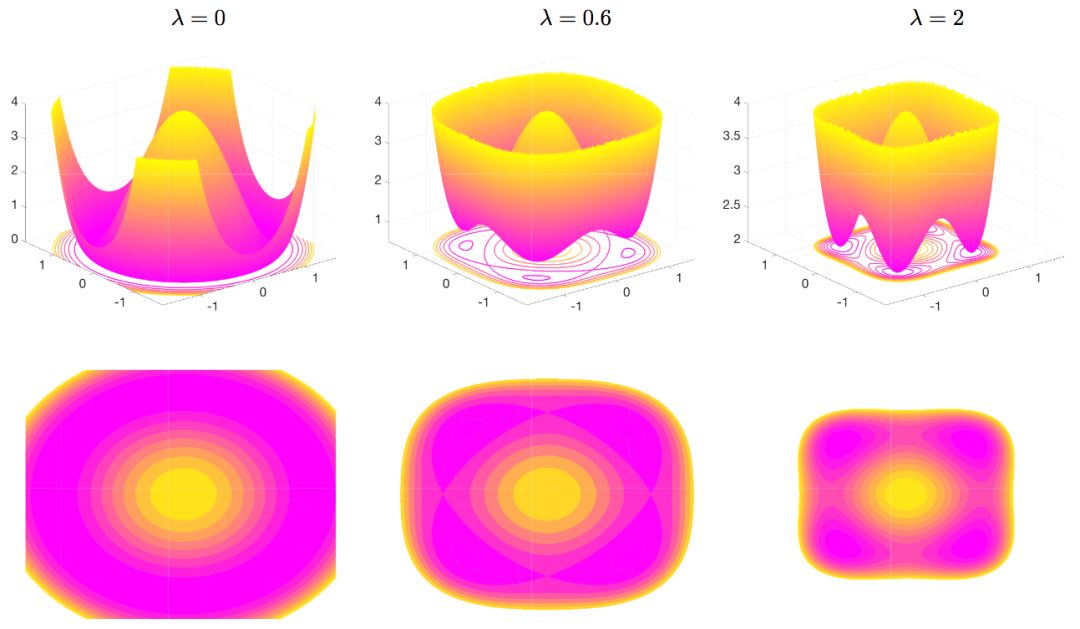
研究人员证明了，如果矩阵U是以上目标的全局最优解，那么U的所有列范数相等。这意味着，dropout倾向于给所有隐藏节点分配相等的权重，也就是说，dropout给整个网络加上了隐式的偏置，倾向于让隐藏节点都具有类似的影响，而不是让一小部分隐藏节点具有重要影响。

上图可视化了参数λ的不同取值的效果。该网络为单隐藏层线性自动编码器，搭配一维输入、一维输出，隐藏层宽度为2。当λ = 0时，该问题转换为平方损失最小化问题。当λ > 0时，全局最优值向原点收缩，所有局部极小值均为全局最小值（证明过程见论文第4节）。当λ增大时，全局最优值进一步向原点收缩。

单隐藏层线性网络

接着，研究人员将上述结果推广到了单隐藏层线性网络。回忆一下，这一网络的目标为：

和权重系联的情形类似，研究人员证明了，如果矩阵对（U, V）是以上目标的全局最优解，那么，‖u_i‖‖v_i‖ = ‖u₁‖‖v₁‖，其中，i对应隐藏层的宽度。

研究人员进一步证明，前面提到的单隐藏层线性神经网络的目标等价于正则化的矩阵分解（regularized matrix factorization）：

利用矩阵分解这一数学工具，研究人员证明了全局最佳值可以在多项式时间内找到：

试验

研究人员试验了一些模型，以印证前面提到的理论结果。

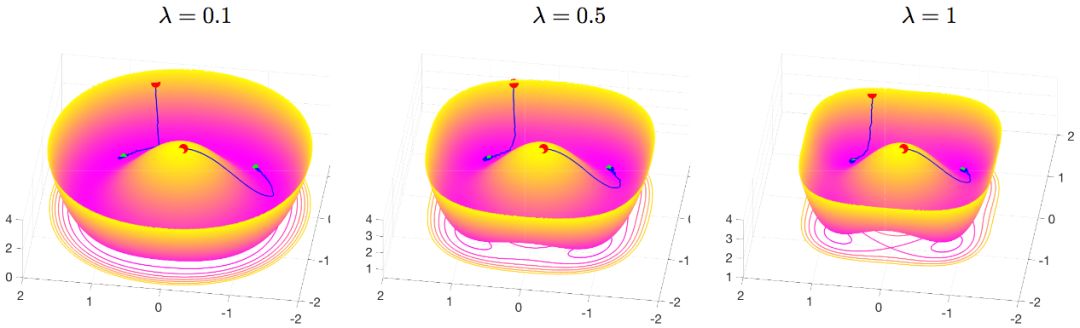
上图可视化了dropout的收敛过程。和之前的可视化例子类似，模型为单隐藏层线性自动编码器，一维输入、一维输出，隐藏层宽度为2。输入取样自标准正态分布。绿点为初始迭代点，红点为全局最优点。从图中我们可以看到，在不同的λ取值下，dropout都能迅速收敛至全局最优点。

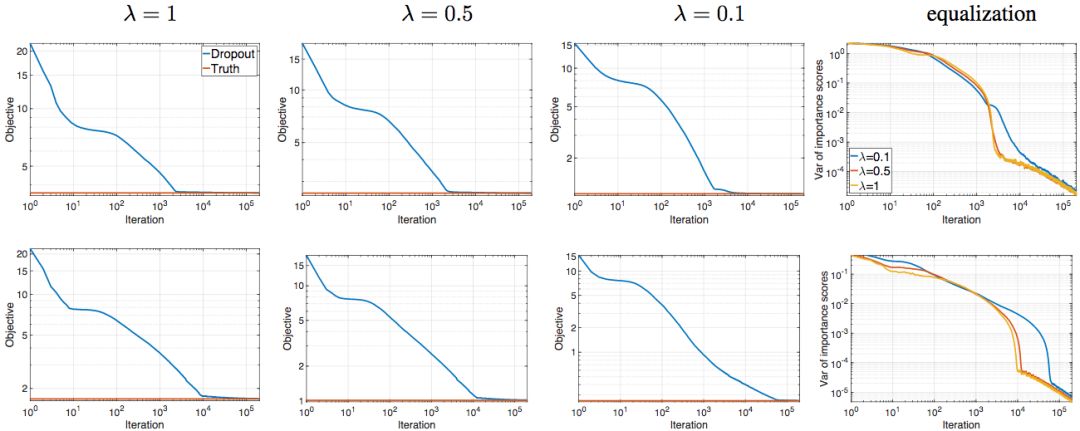
研究人员还在一个浅层线性网络上进行了试验。该网络的输入x ∈ ℝ⁸⁰，取样自标准正态分布。网络输出y ∈ ℝ¹²⁰，由y = Mx生成，其中M ∈ ℝ^120x80均匀取样自右、左奇异子空间（指数谱衰减）。下图展示了不同参数值（λ ∈ {0.1, 0.5, 1}）与不同隐藏层宽度（r ∈ {20, 80}）的组合。蓝色曲线为dropout不同迭代次数下对应的目标值，红线为目标的最优值。总共运行了50次，取平均数。