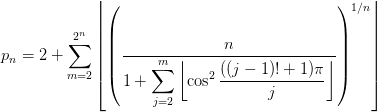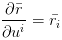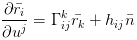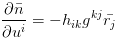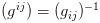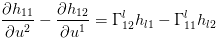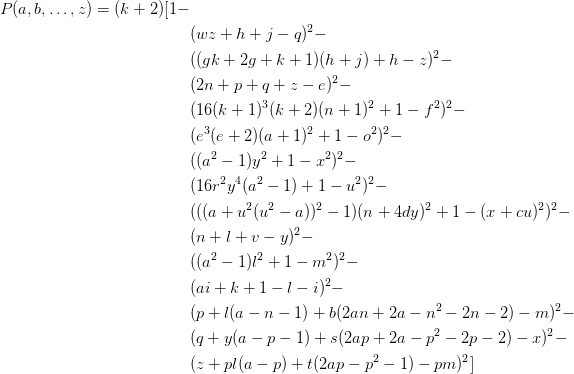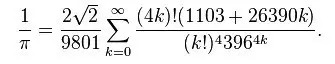数学史上你认为最丑陋的公式是什么？

是丑还是美？

Q：数学上有哪些丑陋的公式？

关于丑没有严格的界定。

A：

@Yu Deng：

以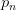表示第n个素数。则

然而并没有什么卵用

@子元：

不是很懂你们物理

@张艺瀚提醒有扩写版

@HopLee：

是时候来个微分几何里的公式了！！！

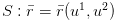
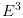
设曲面是中的光滑曲面（符号上面不方便写箭头，我用横杠表示向量了），则有曲面在自然标架下的运功方程：

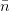
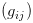
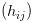
其中为法向量，、分别为曲面第一、第二基本形式系数矩阵，

是第二类Christoffel符号。

引入黎曼曲率张量

（Gauss方程）

（Codazzi方程）

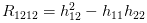
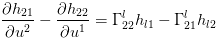
觉得这几个公式很奇怪并且不长不恶心是吧，我是不会告诉你它里面用了爱因斯坦求和约定（两个相同指标就表示求和），有兴趣可以吧每个式子展开写一写（手动微笑）！

初学者一枚，搞微分几何的勿喷

@bigeast：

Jones, Sato, Wada,Wiens 在1976年提出了一个包含26个变量的多项式 ，它的所有正整数值构成了所有的素数，也即。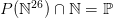

重新输入了公式，然后注意到中括号里面是1减去14个完全平方项，也就是当14个完全平方项都为零的时候，多项式的值才会大于零，从而为素数。

根据维基百科，这个公式其实可以看作是用14个丢番图方程来限制变量k，方程组的解使得k+2为素数。

尝试写个程序验证一下这个公式

https://gist.github.com/bigeast/cc89c8efd9b791440f9d，结果发现几乎所有的值都是负数。因此通过它来寻找或者验证素数都是不实际的。

普通人认为的丑，应该是不需要数学的专业知识也能很快理解公式中的符号，只是不能快速从中找出规律然后记住。如果包含了太多的专业符号，甚至连“丑”也无从谈起了。

Srinivasa Ramanujan（拉马努金） 发现的许多公式就基本上只包含整数之间的初等运算，但又让人很难快速记住，例如：

这种包含着“随机”数字的公式在我看来一点也不妙，但从这些数字竟然能得到。

简直让人想不到！

Ramanujan还有好多类似的包含“随机数字”的与无穷级数、连分数有关的公式，有兴趣不妨去开开眼界。

但哈代发现了这些看似丑陋的公式背后隐藏的数学真理，为这些公式寻找别的数学家能够看得懂的证明（所以天知道Ramanujan是怎么想出这些公式的），于是造就了数学史上的一段佳话。

所以普通人认为“丑”的公式，在数学家看来却别有一番风情呢。

编辑 | Gemini

来源 | 数学中国

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域，经采用我们将奉上稿酬。

投稿邮箱：math_alg@163.com