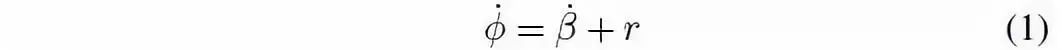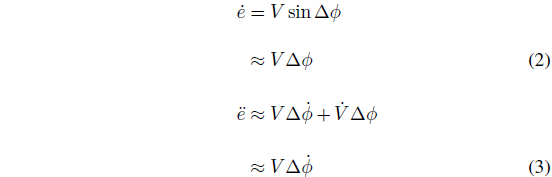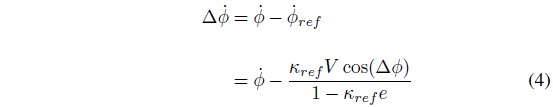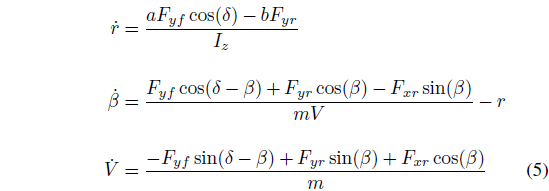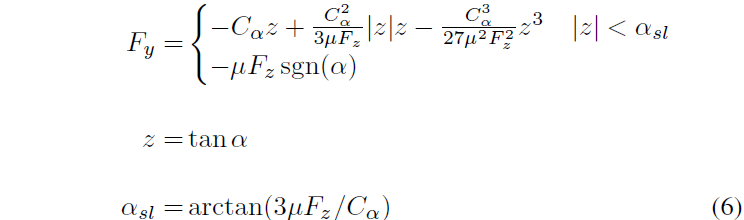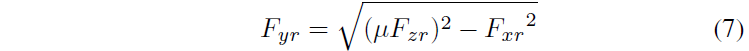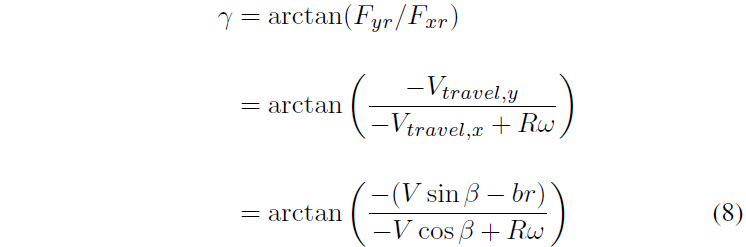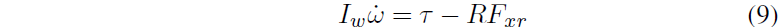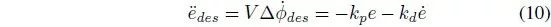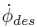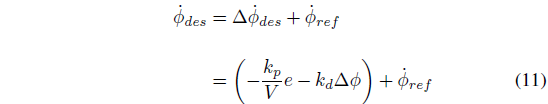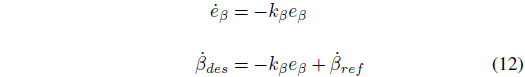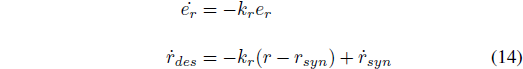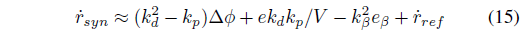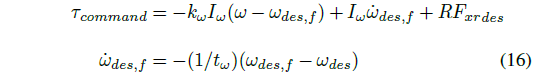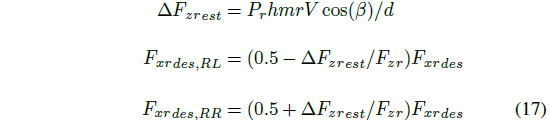斯坦福大学：自动驾驶复杂轨迹工况下的自动漂移控制｜厚势汽车

2018 年 11 月 18 日 厚势

文章译自 AVEC2018 的会议论文《A Controller for Automated Drifting Along Complex Trajectories》，由同济智能汽车研究所集成与控制研究室编译。

原作者：JonathanY. Goh, T. Goel & J. Christian Gerdes

责任编辑：啜小雪

编者按：甩尾、漂移不仅是专业赛车手炫技的技能、众多秋名山玩家的常规操作，也是自动驾驶必须研究的领域。斯坦福大学 Gerdes 教授团队在自动驾驶运动控制领域的研究工作具有标杆意义，本文所述的自动漂移技术将车辆可控范围扩展到稳定性极限之外，可以进一步提升自动驾驶车辆的机动能力。

对自动驾驶车辆的整体安全性和鲁棒性来说，在稳定操控范围外的操纵能力相当重要。因此，本文提出了一种用于复杂轨迹自动漂移的控制器架构。在不假设车辆工作在平衡点附近的情况下，设计了针对非特定路径的控制器，提出了物理上有深刻意义的控制律：采用车辆航向角速度跟踪路径，横摆角加速度用于镇定质心侧偏角，通过非线性模型反演与下层轮速控制相结合，在大范围工况下精确地实现所需求的状态微分。

在全尺寸车辆上进行的实车试验表明，在不同曲率、速度和质心侧偏角下可以很好地跟踪轨迹。

厚势联合 中国汽车产业培训基地 （AIT）推出自动驾驶、新能源汽车精品培训课程，参加本课程，除了学习行业的热点技术和知识，还能结识交大和同济的专家教授、博士和各主机厂的人士。欢迎点击如下链接报名，或联系微信号：autoHS，

电话：‭183 0185 8119‬

1.前言

传统车辆控制架构中通常采用独立的侧向/纵向控制，并且假定车辆处于侧滑动力学稳定范围内。然而，超出车辆的操控极限时会产生强输入耦合和横摆/侧滑不稳定性，导致这种简化方法失效。尽管是完全在车辆稳定性极限范围外操纵的，专业驾驶员在漂移中可以同时实现对车辆侧滑和行驶路径两者的精确控制。自动驾驶漂移控制算法可以将车辆可用状态空间扩展到极限范围外，从而确保自动驾驶车辆最广泛的机动范围。

早期文献中，Velenis[9] 和 Hindiyeh 等人 [4] 分别通过仿真和实验，研究了车辆状态在漂移平衡点下的镇定。因为在标准输入下（转角和驱动力矩）系统是欠驱动的，所以同时跟踪路径和镇定质心侧偏角并不简单。最近的一些研究已经在简单的定圆试验中证明了这一点。Werling 等人 [11] 提出的控制器同时考虑了质心侧偏角镇定和路径跟踪，而 Goh 等人 [3] 的策略则是明确的跟踪路径。但是由于在车辆建模和控制器设计时的进行了严格假设，这些方法不能轻易地扩展到更复杂的轨迹。

已有文献中，关于漂移的研究都使用了在大范围内精确的车辆模型。Ono[6] 和 Voser 等人 [10] 使用了双状态单轨模型研究漂移的不稳定动力学。也有学者将力作为直接输入 [3] [4] 并且对转向和油门延迟进行精确建模 [11] 的三状态单轨模型用于试验验证控制器的设计。Velenis 等人 [9] 基于线性化后的具有稳态载荷转移和车轮动力学的双轨车辆模型，设计了线性二次型调节器。在运动方程的模型精度和可控性之间取得平衡，仍需进一步研究。

与这些方法相比，本文以道路曲线坐标系下的质心侧偏角误差和侧向位移误差作为控制目标，设计了一种用于处理复杂轨迹工况的自动漂移控制器。首先在不需要假设特定的车辆模型或车辆状态处于平衡点附近的情况下，推导出控制器设计所需的动力学模型。由此得到的控制律，用车辆状态微分来表示，十分简单直观。利用漂移时产生的侧偏和横摆动力学解耦：直接采用车辆航向角速度跟踪路径，通过控制车辆横摆角速度相对于航向角速度的快慢，可以同时镇定质心侧偏角。

为了实现这一控制律，需要车辆模型将这些期望的状态微分映射到输入。通过非线性模型反演与下层的轮速控制相结合，实现复杂轨迹下大范围工况的良好准确度，而不是依靠过于简化的假设。在全尺寸测试车辆 MARTY（图 1）上的试验验证了算法在曲率在 1/7 到 1/20m 间变化和速度在 25km/h 到 45km/h 间变化的轨迹以及 -40° 的质心侧偏角工况下的有效性。

图 1 自动漂移测试中的 MARTY 车辆

2.试验车辆与车辆模型

本节首先介绍了在曲线坐标系下的基于力输入的单轨模型的运动方程，然后介绍了轮胎力模型。

2.1 运动方程

2.1.1 路径跟踪状态和动力学

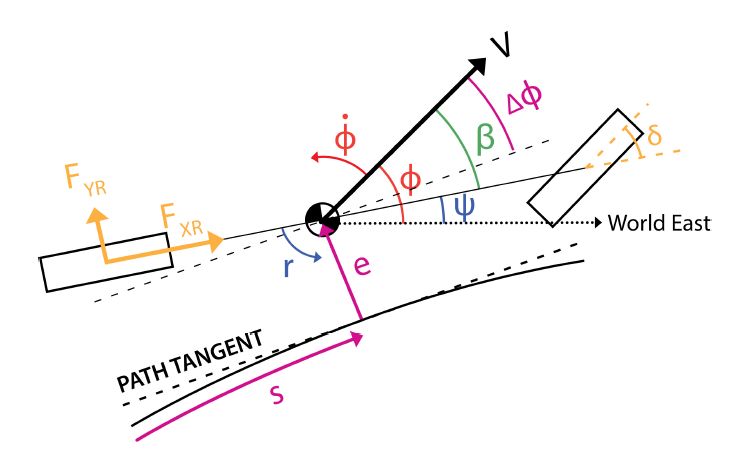
车辆模型如图 2 所示，有三个状态变量：横摆角速度 r、速度 V 和质心侧偏角 β。考虑路径跟踪后，引入了其他几个状态变量。车辆航向角是车辆速度矢量在给定的惯性坐标系的方向，φ 的动力学方程：

图 2 参考路径曲线坐标系下的三状态单轨模型

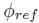
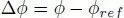
利用曲线坐标系使车辆跟踪参考轨迹，侧向位移误差 e 是车辆质心到参考轨迹的最近点的距离，s 是沿路径到这个点的距离。参考航向角是 s 处路径相对于惯性坐标系的正切角，航向角误差，是车辆航向角与参考航向角之差。e的动力学方程表示为：

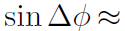
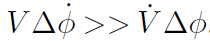
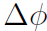
进行一些简化假设：和，由于闭环控制中逐渐变小，因此假设合理。

最后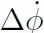，的动力学方程为

其中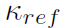是参考轨迹在 s 处的曲率。

2.1.2 车辆状态和动力学

基于如图 2 所示的单轨自行车模型进行非线性车辆模型反演，其中作用于车辆的力包括前轴侧向力 Fyf，后轴侧向力 Fyr 和后轴纵向力 Fxr，运动方程为：

其中 δ 为转向角，a，b 分别是前后轴到质心的距离，m 是车辆质量。

2.2 前轴轮胎力建模

前轴侧向力 Fyf 采用 Fiala 刷子轮胎模型 [2] 表示，文献 [3] [4] 中的漂移控制器中也采用了该模型。

其中 Fz 是轮胎垂向载荷，Cα 是侧偏刚度，α 是侧偏角，μ 是轮胎附着系数。

2.3 后轴轮胎力建模

漂移时，整个后轮轮胎接地面处于完全滑动的状态。假设各向同性摩擦系数，侧向力和纵向力受摩擦圆关系约束：

文献 [3] [4] 控制算法设计时通过摩擦圆建立期望的后轴侧向力 Fyf 与后轴纵向力 Fxr 映射关系，直接将后轴纵向力作为系统输入并乘以轮胎半径得到后轴转矩需求。

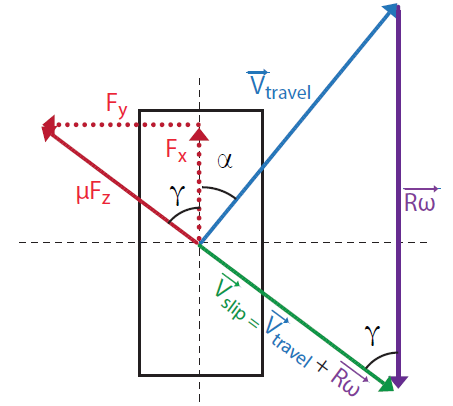
该方法忽略了车轮动力学，但当考虑更复杂轨迹工况时车轮动力学是相当重要的；Fxr 不是真正的输入，而是轮胎与路面滑移的结果。对于完全饱和的轮胎，力和滑移的关系可以以一种既简单又有物理意义的方法进行建模：力大小为 μFz，其方向与滑移速度矢量 Vslip 方向相反。定义这个方向为推力角 γ，如图 3 所示，改变 Rω 矢量的长度可以直接改变 γ。几何关系为：

其中 R 是轮胎半径，ω 是轮速，Vtravelx 和 Vtravely 分别是车辆在轮胎处速度的纵向和侧向分量。

图 3 滑移轮胎的速度和力矢量

值得注意的是在完全饱和状态下，这个关系同刷子轮胎模型 [7] 和简化魔术公式轮胎模型 [1] 表达是一致的。系统的控制输入，在车轮动力学 ω 中表达为：

其中 Iω 是车轮-轮胎-传动系统的转动惯量，τ 为实际转矩。

3.控制器设计

3.1 概述

控制器的任务是利用转向角和后轴驱动力矩跟踪给定路径和期望质心侧偏角。因此选择了侧向位移误差 e 和质心侧偏角 β 作为控制变量。

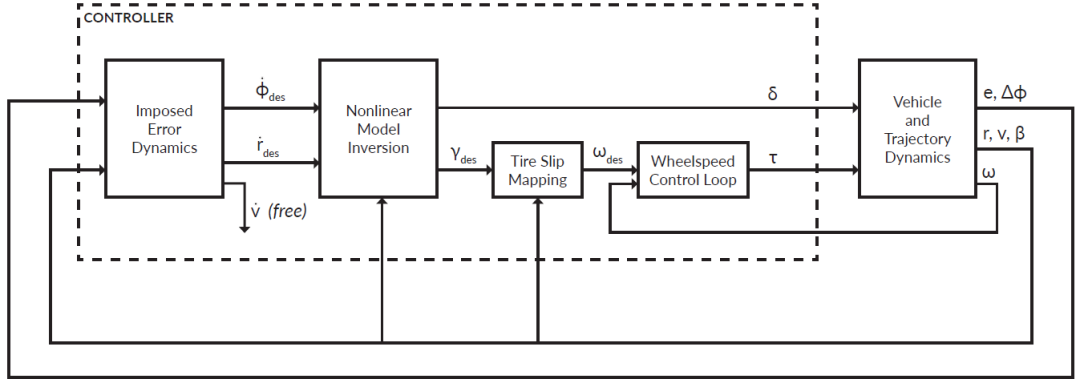
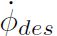
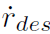
控制器的总体结构如图 4 所示，在第一部分，基于 e 和 β 的期望稳定动力学，得到期望的航向角速度和综合横摆角速度 rsyn，对 rsyn 闭环得到期望的横摆角加速度。

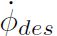
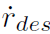
第二部分，通过非线性车辆动力学模型反演将和转化为转向角 δ 和期望的推力角 γdes。然后将推力角映射到期望的轮速 ωdes。最终，对 ωdes 闭环得到驱动力矩τ。

图 4 控制器架构框图

3.2 误差动力学

3.2.1 路径跟踪

航向角速度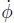直接用于跟踪路径。侧向位移误差 e 的期望二阶动力学方程为：

得到期望的:

3.2.2 镇定质心侧偏角

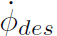
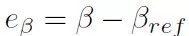
然后，与相关的车辆横摆角速度，用于镇定质心侧偏角。质心侧偏角跟踪误差的期望一阶动力学方程：

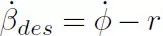
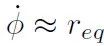
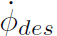
与文献 [3] [4] 中方法类似，基于综合输入横摆角速度 rsyn 计算得到期望的，这些方法进行了的稳态近似，然后，由于对航向角速度有明确的控制，使用期望的航向角速度替代。

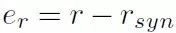
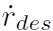
对横摆角速度跟踪误差的一阶求导，得到期望的横摆角加速度。

其中是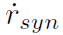综合横摆角速度的微分，可以近似表达为：

其中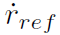是参考轨迹的横摆角加速度。

3.3 非线性模型反演

通过公式（5）中非线性单轨车辆模型反演，将期望变换为转向角和后轴纵向力/推力角。

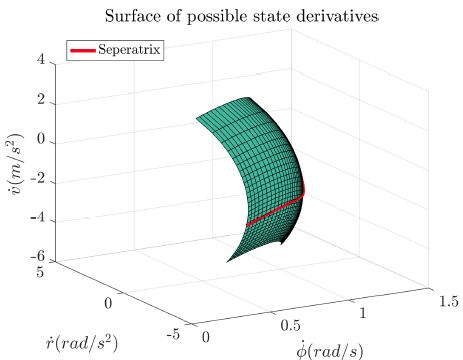
图 5 中是一组比较有代表性的状态微分间曲面关系。投影到平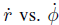面（图 6），可以看到曲面发生折叠即部分区域对于给定组合有两个解。这样把曲面分成较大的「上」表面和较小的「下」表面；分界线如图 5、6、7 中红线所示。

图 5 横摆角速度为 53.9°/s,车速为 9.35m/s,质心侧偏角为 -40° 时车辆状态微分间三维图

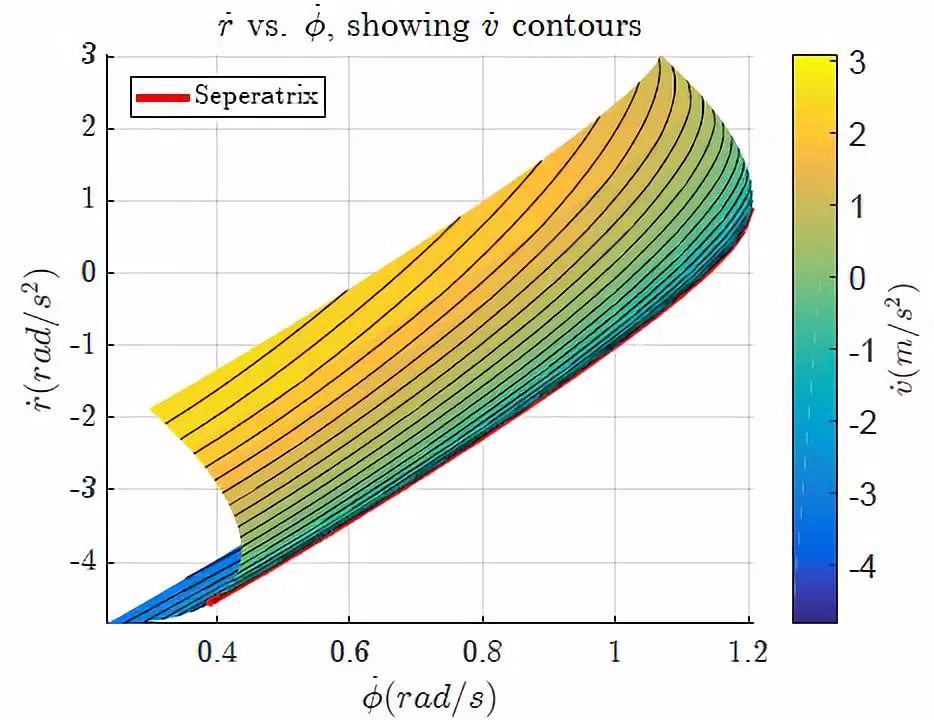
图 6 沿车速微分等高线的横摆角加速度vs航向角速度

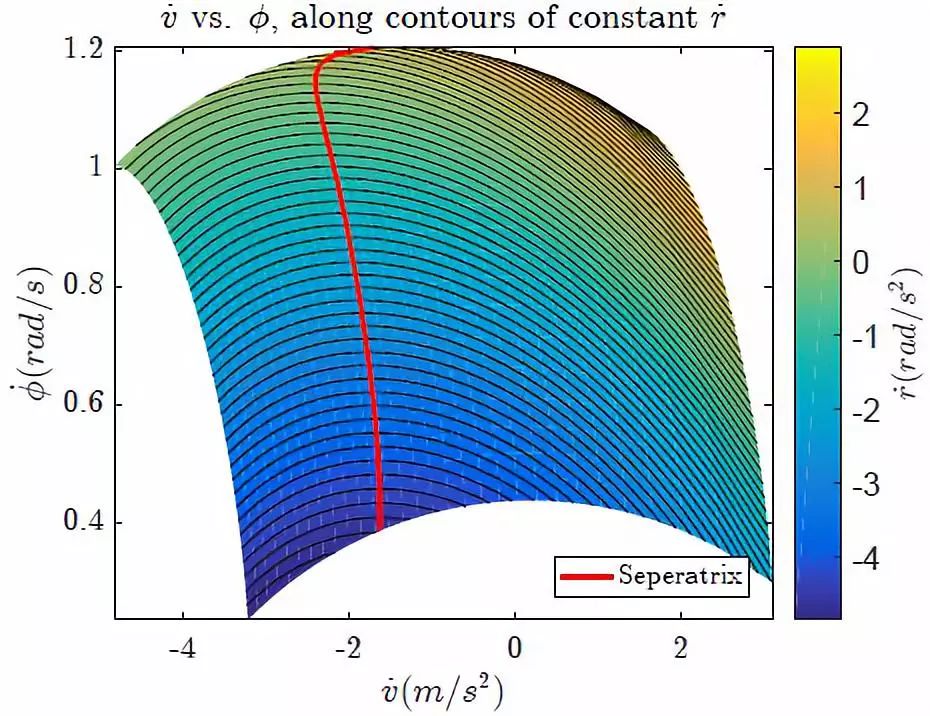
图 7 沿横摆角加速度等高线的航向角速度 vs 车速微分

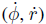
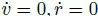
通常来讲，仅有小部分空间是位于下表面的，因此模型反演可以在上表面约束下得到 1 对 1 的映射关系，并以简单的方式确保执行器指令的连续性。另外值得注意的是，上表面通常包括状态组合，如图 7 所示，在跟踪准平衡轨迹时能实现此状态微分空间。

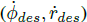
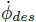
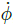
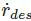
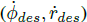
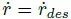
需求的有可能落到可行域外。对控制器中初始时刻和试验中产生的这种情况进行简单处理。的值受到可行域的饱和约束，然后计算。得到的沿线投影到可行域内。所提出策略中不稳定的横摆/侧偏动力学控制优先级高于侧向位移误差控制。

3.4 轮速控制

根据非线性模型反演得到的后轴纵向力/推力角,进而根据公式（8）中的力-滑移关系得到期望轮速。基于简化的动态面控制 [3] 跟踪期望轮速 ωdes。

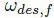
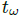
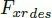
其中是期望轮速在时间常数为的一阶滤波后得到的，利用期望后轴纵向力计算前馈力矩。

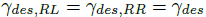
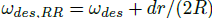
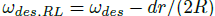
因为 MARTY 测试车辆后轮独立可控且机械上解耦，分别对左右后轮进行控制。令左后轮和右后轮的推力角分别为，得到期望的左右轮和右后轮轮速和，其中 d 为车辆轮距，单轮的期望纵向力基于稳态载荷转移的假设得到：

其中为发生在后轴的载荷转移的经验值，h 为质心高度。

4 试验验证

在曲率在 1/7 到 1/20 间变化和速度在 25km/h 到 45km/h 间变化的复杂轨迹以及 -40° 的参考质心侧偏角下试验验证了算法的有效性。

4.1 测试方法

试验在如图 1 所示的试验平台 MARTY 上进行。MARTY 由 1981 DMC Delorean 改装而来，配备有线控转向和可独立驱动左右后轮的电驱动系统。车辆状态信息通过集成的 RTK-GPS/IMU 得到，更新频率为 250Hz。在上位机实时运行的控制算法的运算频率也为 250Hz。

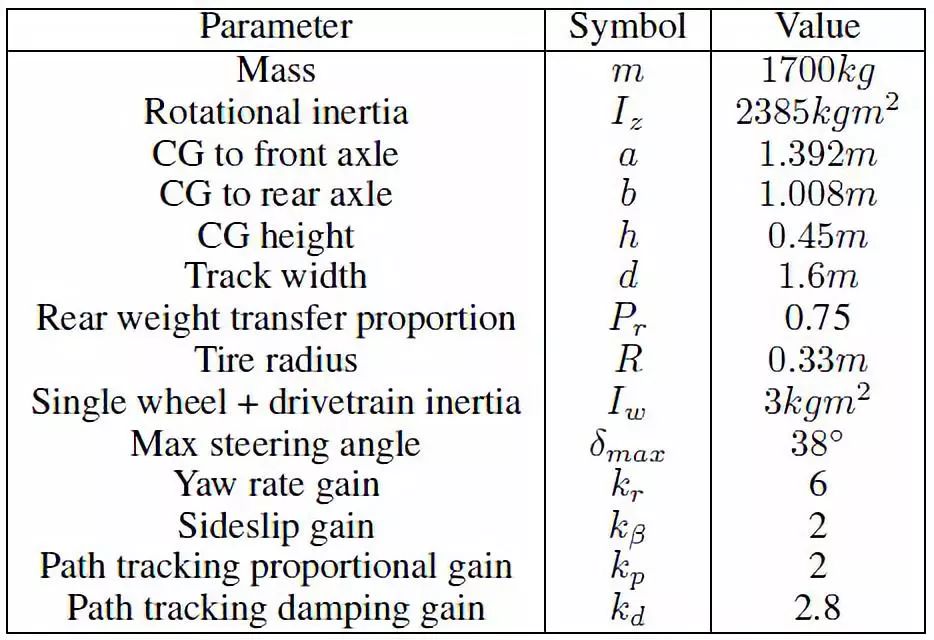
在参考轨迹的起始点和末端分别增加简单的进入和退出回旋线，用于文献 [5] 相似的基础路径跟踪控制器使得车辆跟踪此路径。漂移控制器在 s=57m 时介入，在 s=463m 时退出。控制器参数和车辆参数如表 1 所示。

表 1 控制器参数和车辆参数

4.2 轨迹规划

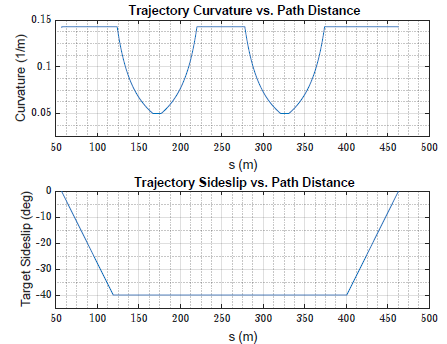
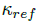
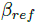
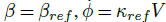
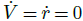
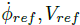
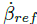
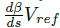
参考文献 [5] 方法，轨迹是由不稳定漂移平衡点序列构成的。首先，选取期望曲率和质心侧偏角，其是关于路径距离 s 的函数。对于参考轨迹中每个点，将和代入运动方程求解得到参考轨迹值，参考质心侧偏角近似表示为。

选取的配置文件曲率从 1/7 到 1/20m 间变化，参考质心侧偏角为 -40°，得到平衡速度在 25km/h 到 45km/h 之间的轨迹。

图 8 轨迹曲率与参考质心侧偏角配置

4.3 试验结果

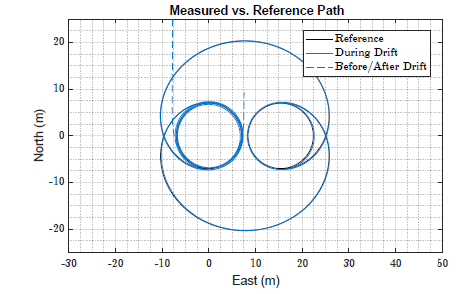
控制算法较好地跟踪了参考轨迹，表现出良好的侧向位移误差和质心侧偏角跟踪效果。

如图 9 所示，车辆的实际路径与参考路径十分接近，图 10 给出了侧向位移误差与路径距离的关系：其均方根误差为 0.18m，最大偏差为 -0.36m。

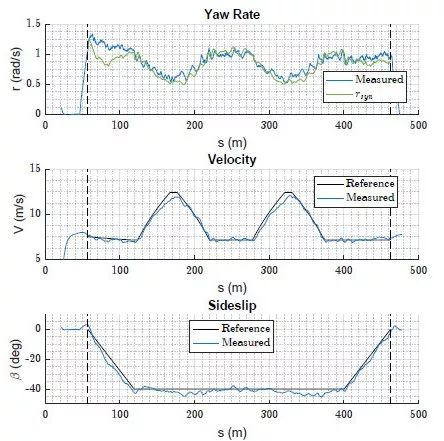
车辆处于期望质心侧偏角 -40° 附近状态时，达到了上述良好路径跟踪性能。图 11 给出了测量的车辆状态，可以看出质心侧偏角跟踪效果较好：均方根误差为 2.4°，最大偏差仅为 -6.1°。闭环下速度也与轨迹参考速度十分接近，既说明了车速稳定又说明了用于规划的模型比较准确。除了在漂移起始时刻，测量的横摆角速度也可以很好地跟踪参考横摆角速度。

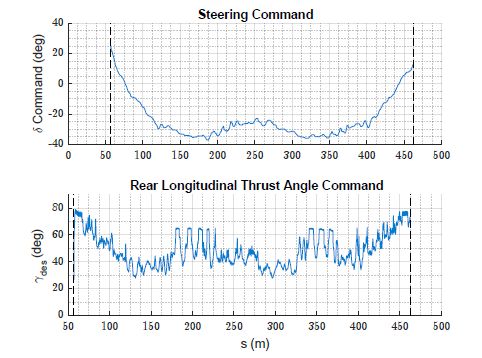
最后值得注意的是，因为在较大的状态范围内进行非线性模型反演，会产生较大范围的输入-最明显的例子是控制算法在图 6 测试时达到了 65°。

图 9 试验中测量路径vs参考路径

图 10 试验中路径跟踪性能

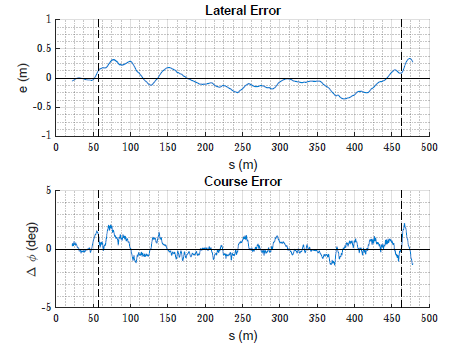
图 11 试验中车辆状态 vs 路径距离

图 12 试验中转向角和推力角输入

5.结论

本文设计了针对复杂轨迹的自动驾驶漂移控制器。控制器由车辆状态微分推导所得，并且没有涉及到特定的车辆模型。航向角速度用于跟踪曲线坐标系下的侧向位移误差，然后控制相对于航向角速度的横摆角速度从而控制质心侧偏角。

为了得到车辆状态微分到执行器输入的映射关系，进行非线性模型反演和简单的轮速闭环控制。试验验证了在曲率在 1/7 到 1/20 间变化和速度在 25km/h 到 45km/h 间变化的复杂轨迹以及 -40° 的参考质心侧偏角工况下的有效性。

对复杂轨迹下漂移平衡点的路径跟踪和质心侧偏角镇定研究，保证了自动驾驶车辆在需要的情况下能够在开环稳定极限外操纵。未来的研究将进一步考虑在未进行准平衡假设下实现轨迹规划和跟踪，解决车辆状态快速变化的问题。

6.参考文献

[1]Egbert Bakker, Lars Nyborg, and Hans B Pacejka. Tyre. modelling for use in vehicle dynamics studies. Tech. rep.SAE Technical Paper, 1987.

[2]E Fiala. “Seitenkrafte am rollenden Luftreifen”. In: ZVDI 96 (1954), Nr–29.

[3]Jonathan Y Goh and J Christian Gerdes. “Simultaneous stabilization and tracking of basic automobile drifting trajectories”. In: Intelligent Vehicles Symposium (IV), 2016 IEEE. IEEE. 2016, pp. 597–602.

[4]Rami Y. Hindiyeh and J. Christian Gerdes. “A Controller Framework for Autonomous Drifting: Design, Stability, and Experimental Validation”. In: Journal of Dynamic Systems, Measurement, and Control 136.5 (July 2014), p. 051015.

[5]Krisada Kritayakirana and J. Christian Gerdes. “Autonomous Vehicle Control at the Limits of Handling”. In: International Journal of Vehicle Autonomous Systems 10.4 (2012), pp. 271–296.

[6]E. Ono, S. Hosoe, H.D. Tuan, and S. Doi. “Bifurcation in Vehicle Dynamics and Robust Front Wheel Steering Control”. In: Control Systems Technology, IEEE Transactions on 6.3 (May 1998), pp. 412–420.

[7]Jacob Svendenius. “Tire Modeling and Friction Estimation”. PhD thesis. Lund University, 2007.

[8]D Swaroop, J Karl Hedrick, Patrick P Yip, and J Christian Gerdes. “Dynamic surface control for a class of nonlinear systems”. In: IEEE transactions on automatic control 45.10 (2000), pp. 1893–1899.

[9]Efstathios Velenis, Diomidis Katzourakis, Emilio Frazzoli, Panagiotis Tsiotras, and Riender Happee. “Steadystate drifting stabilization of RWD vehicles”. In: Control Engineering Practice 19.11 (2011), pp. 1363–1376.

[10]Christoph Voser, Rami Y. Hindiyeh, and J. Christian Gerdes. “Analysis and Control of High Sideslip Manoeuvres”. In: Vehicle System Dynamics 48.sup1 (2010), pp. 317–336.

[11]Moritz Werling, Philipp Reinisch, and Lutz Gr¨oll. “Robust power-slide control for a production vehicle”. In: International Journal of Vehicle Autonomous Systems 13.1 (2015), pp. 27–42.

厚势小百科

同济智能汽车研究所

同济大学智能汽车研究所位于同济大学嘉定校区，聚焦智能型新能源汽车，围绕 智能驱动系统、V2X 与组合定位、智能感知与控制、线控底盘、智能汽车测试与评价 五个技术方向，开展深入应用基础研究。目前共有研发人员 107 人，其中 973 计划首席科学家/长江学者创新团队带头人 1 人，国家千人计划专家 2 人，教授 5 人。

所长为余卓平教授。余卓平同时也是同济大学校长助理、中国汽车工程学会副理事长，国家 973 计划项目首席科学家。熊璐教授担任执行所长。

-END-

文章精选

智能驾驶

新能源汽车