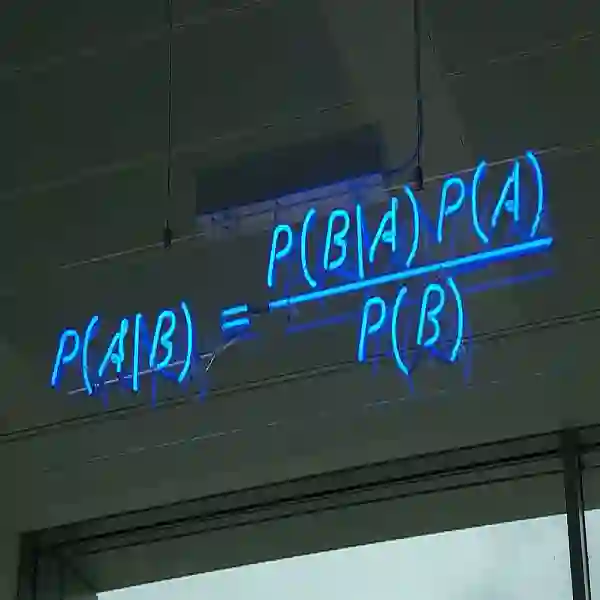指导工作与生活的《算法之美》:用贝叶斯法则预测未来 II
数学家的结论:
确定一个前提条件,
算法就能提供简单有效的
生活建议。
下文节选自《算法之美:指导工作与生活的算法》, 已获出版社授权许可, [遇见数学] 特此表示感谢!
贝叶斯法则与先验信念
可以想象,所有这些假设都是一致并可以想象的。为什么我们要偏向其中一种,而这一种并不比其余的更一致或可以想象?
——大卫•休谟
拉普拉斯也考虑了另一种修饰贝叶斯理论的方法,这将被证明是至关重要的:那就是如何处理那些比其他假设可能性更大的假设。例如,买彩票时,99%的中奖率是有可能的,但我们可以假设中奖率更有可能只有1%。这一假设应该体现在我们的估算过程中。
说得更具体点儿,例如有一个朋友给你看两个不同的硬币。一个是正常的“公平”硬币,正反两面都具有50–50的概率,另一种是两面都是头像的硬币。他把它们扔到一个袋子里,然后随意地拿出一个,他将硬币旋转一次:是头像。你认为你的朋友旋转的是哪个硬币?
贝叶斯的反向工作方案使这个问题变得简单。那个公平硬币转到头像的概率是50%,另一个双头硬币转到头像的概率是100%。因此,我们可以自信地断言,转到这个硬币的概率是100%除以50%,或朋友掏出双头硬币的概率是它的两倍。
现在考虑下面一次的旋转。这一次,朋友给你看9个公平硬币和一个双头像硬币,把所有10枚硬币都装进袋子,随机抽取一个,并翻转它:还是头像。现在你怎么想?这次是公平硬币还是双头像硬币?
拉普拉斯预料到了这一点,而且答案又一次简单得令人印象深刻。如果和以前一样,一枚公平硬币转到头像的概率正好是一枚双头像硬币的一半。但现在,首先公平的硬币被抽到的概率就是双头像硬币的 9 倍。事实证明,我们可以把这两个不同的概率都考虑进去,并把它们相乘:这就是说,你朋友持有一个公平的硬币的概率是双头像硬币的 4.5 倍。
描述这种关系的数学公式,将我们先前持有的观念和我们眼前的证据结合起来,就形成了后来的贝叶斯法则。有点儿讽刺的是,真正重要的工作却是由拉普拉斯完成的。它提供了一个非常简单的解决方案来如何处理现有的信念与观察到的证据:将它们的概率相乘。
值得注意的是,有一些预先存在的信念,在计算这个公式时至关重要。如果你的朋友只是走近你说:“我从这个袋子里翻出了一枚硬币,最后转出头像那面。你认为这是一枚公平硬币的概率有多大?”除非你最开始就对袋子里是什么硬币有一定了解,否则你完全无法回答这个问题。(当你对任何一个概率都无从得知的时候,你便无法将两个概率相乘),在硬币翻转之前,你对“袋子里”是什么的感觉,或是说在你看到任何数据之前,每个假设的概率都是真实可能的,这就是所谓的先验概率,或者简称为“先验”。贝叶斯法则总是需要一些先验,即使它只是一个猜测。有多少枚双头像硬币?抽到他们的概率有多大?那么,你的朋友有多大可能是一个骗子呢?
贝叶斯法则依赖于先验概率,这一点在历史上的某些时刻被认为是有争议的、有偏见的,甚至是不科学的。但在现实中,我们的头脑实际上很少会进入一个完全空白甚至停滞的状况。
当你对先验概率有一定的预估时,贝叶斯法则也适用于各种各样的预测问题,无论它们是大数据类型还是更常见的小数据排序。计算彩票获奖概率或扔硬币的概率仅仅是开始。由贝叶斯和拉普拉斯研究出的方法可以在任何时候帮助我们,尤其是当我们遇到不确定性或数据不足的问题和工作时。这正是我们试图预测未来时所面对的情况。
哥白尼原则
预测本就是一件难事,预测未来尤其如此。
——谚语
当理查德·戈特看到柏林墙时,他问了自己一个非常简单的问题:我在哪?也就是说,在这一人工建筑存在的全过程中,我是否恰好已经到达了呢?简而言之,他是在从时间角度问一个空间问题,而这一问题正是在400年前深深吸引着天文学家尼古拉·哥白尼的问题:我们在哪?地球在宇宙的什么位置?与前人不同,哥白尼激进地以为地球不是宇宙的中心,也就是说地球没有什么特别的。戈特决定采取同样的关于时间的分析步骤。
他设想,他到达柏林墙的那一刻并不特别,因为这只是柏林墙整个历史中的一瞬。如果有任何一个时刻都有同样的可能性,那么平均来说,他的到来应该是在一个精确的中间点(因为他有50%概率是在此之前到来,或50%的概率是在此之后)。更普遍的是,除非我们确定我们在某个特定时间现象中出现的特定中间点。如果我们假设我们到达的中间点有精确的时间,那么对于它在未来还可以持续多久的最佳猜测就变得很明显:确切地说就是它已经存在的时间。戈特看到柏林墙时已经建成8 年了,所以他最好的猜测是,它将再存在8 年。(最终,这个数字是20 年。)
图自网络
这个简单的推理,被戈特称为哥白尼原则,它可以得出一个简单的算法,能为各类事件做出预测判断。在没有任何先入为主的预测时,我们不仅可以用它来获得对柏林墙终结时间的预测,同时也可以预测任何其他短期和长期现象。哥白尼原则预测道,美利坚合众国作为一个国家将一直持续到2255 年左右,谷歌将持续到大约2032 年,你与你的朋友一个月前开始的一段关系将可能再持续约一个月(也许你该告诉他不要参加刚收到的婚礼邀请呢)。同样,它告诉我们要持怀疑态度,例如,《纽约客》杂志封面是一个人拿着一个6 英寸的智能手机,上面有大家熟悉的网格正方形应用程序图标,标题为“2525”。但这是令人怀疑的。据我们所知,智能手机刚诞生10 年,哥白尼原则告诉我们,它不可能出现在2025 年,更别说5 世纪后了。到2525年,即使还有一个纽约市存在,也会让人感到吃惊。
更实际地说,如果我们正在考虑一份建筑工地的工作,他们的标牌表明“上一次工程事故发生在7 天前”,我们可能会想离开,除非这是一份我们计划做得特别短的工作。如果一个城市的公交系统承担不起可以告诉乘客下一班车什么时候会到来这一非常有用却很昂贵的实时提醒系统的话,哥白尼原则表明,可能有一个更简单也更便宜的替代品。那就是简单地显示前一辆公交车到达此处的时间距离现在有多久,这可以为判断下一辆公交车到来的时间提供一个实质性的提示。
但是哥白尼原则就一定正确吗?当戈特在《自然》杂志上发表了他的猜想之后,该杂志收到了很多重要信件。当我们尝试将规则应用到一些比较熟悉的例子时,很容易理解这是为什么。如果你遇到一个90岁的男子,哥白尼原则预测他会活到180岁。同时,每个6岁的男孩都会被预测将在12岁时早逝。
要理解为什么哥白尼原则是合理的,以及为什么它有时不合理,我们需要回归到贝叶斯法则。因为,哥白尼原则尽管具有明显的简单性,但其的确是贝叶斯法则的一个实例。
贝叶斯与哥白尼
在预测未来时,如柏林墙的寿命这类问题,我们需要评估的假设是所有手头上掌握的现象的持续时间:它会持续一个星期,一个月,一年,还是十年?正如我们已经看到的,要应用贝叶斯法则,我们首先需要给每个现象的持续时间分配一个先验概率。事实证明,哥白尼原则正是应用贝叶斯法则并使用了所谓的无信息先验的结果。
起初,这似乎是一个矛盾。如果贝叶斯法则总是要求我们明确事先的预测和想法,我们又怎么能告诉它,我们没有任何预测结果呢?在彩票抽奖的情况下,为无知进行辩护的一个方法就是被称为“统一先验”的方法,这就是认为每个中奖彩票的比例都是相同的。在柏林墙这一例子中,无信息先验意味着:我们对将要预测的时间范畴一无所知:墙可能会在接下来的 5 分钟或 5 年后倒塌。
除了这些无信息先验,如我们所见,我们供应给贝叶斯法则的唯一一部分数据,事实上就是我们到达柏林墙的时候,它已经存在了 8 年。任何预测它小于 8 年寿命的假设都可以被排除,因为这些假设不能解释我们这里的情况。(同样的,一枚双头像硬币就可以排除字那面的可能性。)任何超过 8 年的预测都是有可能的,但是如果柏林墙要存在 100 万年,那它将是一个很大的巧合,表明我们几乎是接近它存在的最初起点。因此,即使特别长的寿命不能排除,但它也不大可能出现。
当贝叶斯法则与所有这些概率结合——更有可能的短时限就拉低了平均预测,可能性更小但也有一定可能性的长时限又将其拉高,哥白尼原则便出现了:如果我们要预测某个事物还将持续存在多久(在对它没有其他任何了解时),我们可以做出的最好的猜测就是,它将再持续已经存在的时间。
事实上,戈特并不是第一个提出类似哥白尼原则的人。20 世纪 20 年代中期,贝叶斯统计学家哈罗德·杰佛利曾考虑仅仅通过一辆城市有轨电车的序号来确定一个城市有轨电车的数量,并得出了相同的答案:该数字的双倍。一个类似的问题出现得更早,在第二次世界大战期间,同盟国试图估计由德国制造的坦克数量。他们通过所捕获的坦克的序列号,在纯数学估计的基础上进行预测,得出的结果是德国每月生产246 辆坦克,而通过广泛的(高度危险的)空中侦察所获得的估计表明,这个数字更接近于1400。而战后,德国记录显示的真实数字是:245。
在认识到哥白尼原则是无信息先验基础上的贝叶斯法则之后,就可以回答很多关于其有效性的问题。哥白尼原则在我们什么都不知道的情况下似乎是合理的、准确的,如在1969年看到的柏林墙,我们不确定什么时间范畴是合适的。同时,在我们对某一对象的确有所了解时,就会感觉这是完全错误的。预测一个90岁的人能活到180岁是不合理的,这恰恰是因为我们关于人类寿命已经了解了很多——在这种情况下,我们就可以预测得更好。我们给贝叶斯法则带来的先验信息越丰富,我们便能从中得到越有用的预测。(未完待续)